ある波面と、位相分布が同じで進行方向が逆の波面を位相共役波(Phase- conjugated wave)と呼びます。ここでは反射型位相共役波の表現方法について紹介します。
位相共役波の表現方法について
Best answer by Kensuke.Hiraka
反射型位相共役波の表現方法について紹介します。
透過型位相共役波の表現方法は以下のリンクをご参照ください。
以下の光学系を例として考えます。
入射ビームは直径50mmの平面波です。
面1、2は平行平面板ですが、面2はイレギュラ面で2μmの面形状の歪みがあります。
面3は平面鏡で、ビームを折り返しています。
面4、5で定義された平行平面板は、面1、2の平行平面板と同じ形状です。
よって、これはダブルパス光学系です。
右端が平面鏡、左の板が平行平面板、左端が像面です。
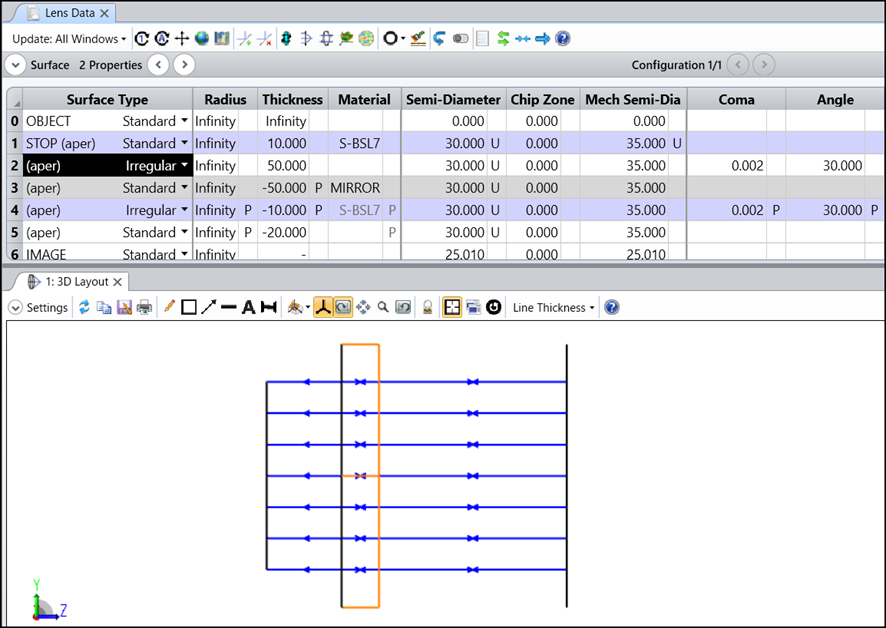
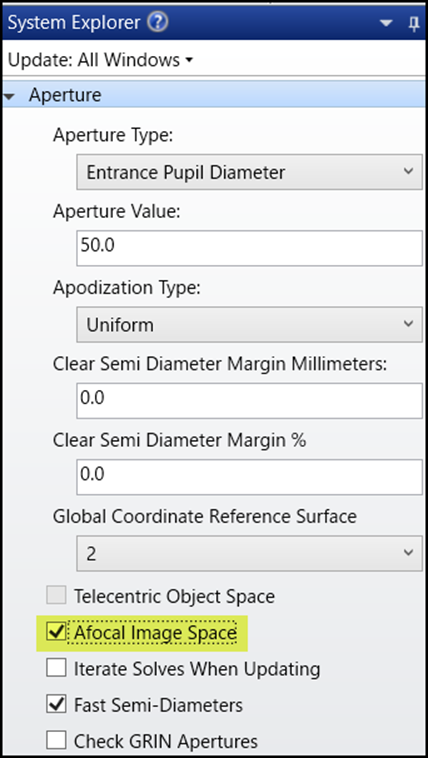
出射ビームは平面波なので、以下のように「アフォーカル像空間」を使用して評価します。
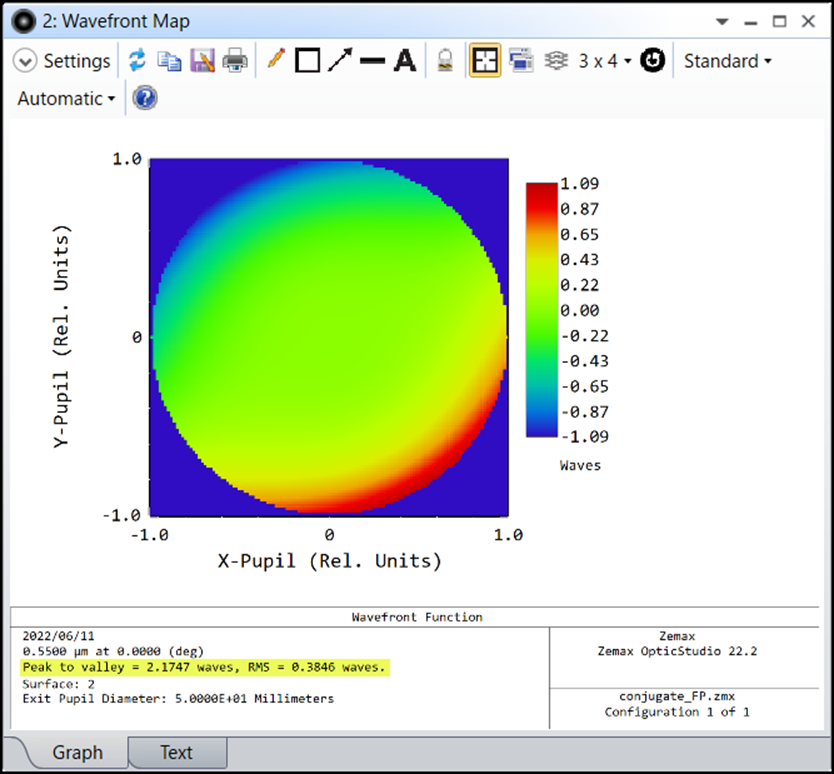
面2を通過後の波面が以下となります。RMS値で0.38λの波面収差があります。
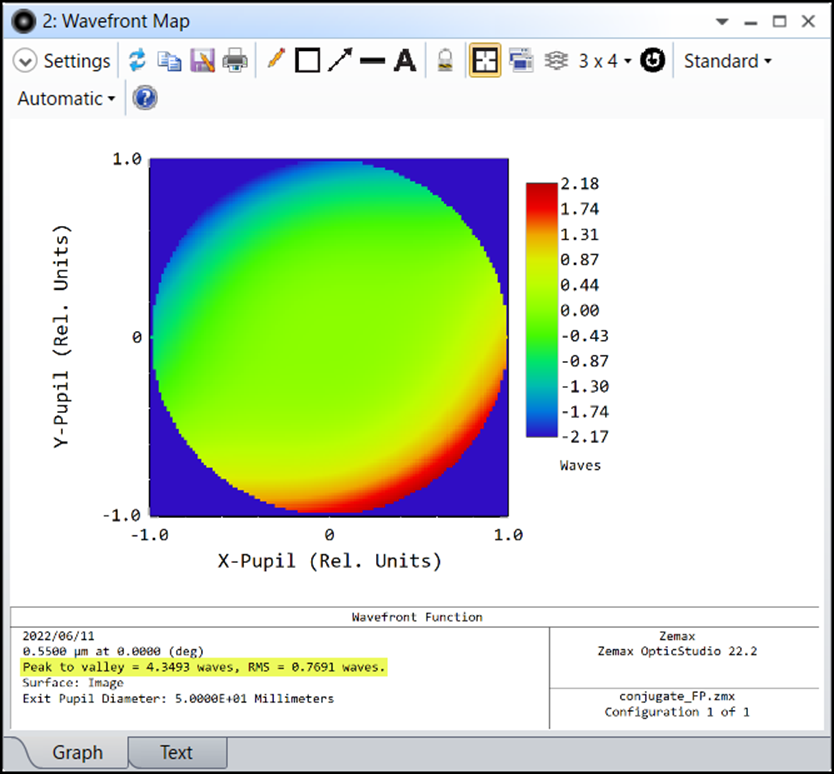
平面波で反射し、再度平面板を通過した後(像面)の波面は以下となります。波面の歪みが加算され、RMS値が0.77λとなっています。
以上が通常のダブルパス光学系になります。
OpticStudioには、以下の再帰反射面(Retro Reflect)が用意されています。
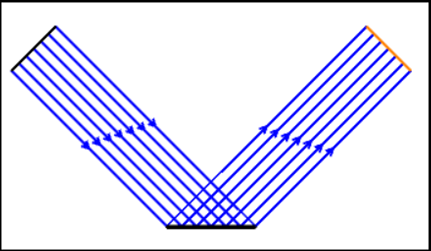
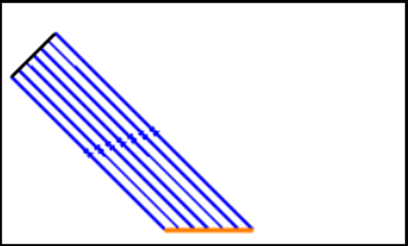
通常のミラーは以下の上図のように反射しますが、再帰反射面は下図のように反射します。
再帰反射面は、位相共役波を発生させる「位相共役鏡」として使用できます。面3の面タイプを以下のように変更します。
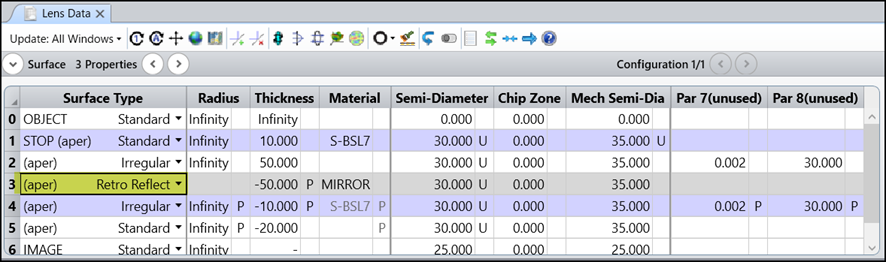
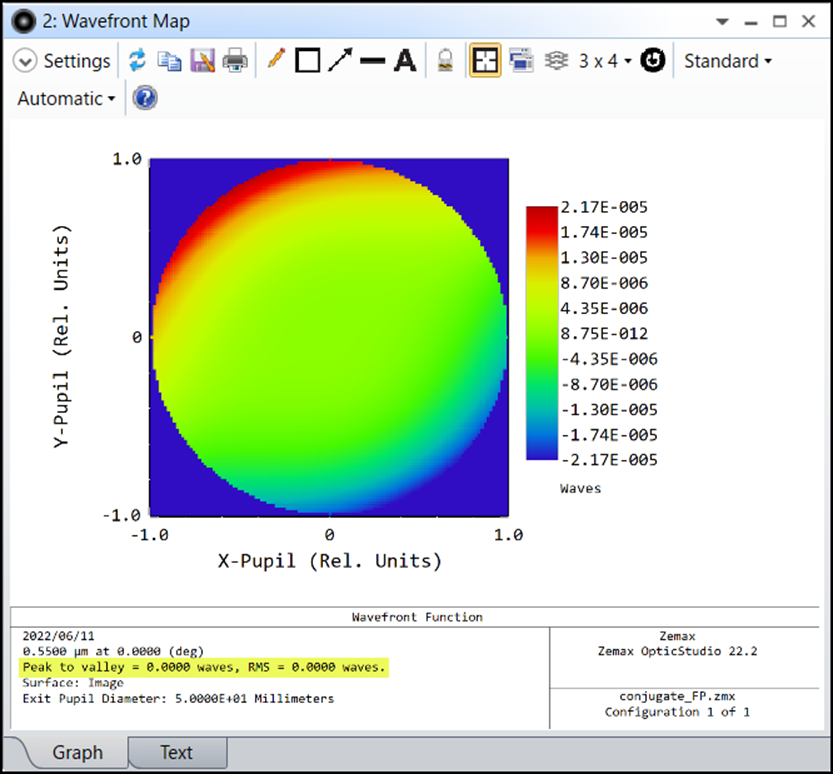
そうすると、面3で反射した光は、面3に入射する光の「位相共役波」になります。そのため、ダブルパス光学系を通過して同じ位相変調を受けると、元の平面波に戻ります。以下は像面における波面で、元の波面収差0の平面波に戻っていることが確認でき、面3が「位相共役鏡」として機能していることが分かります。
今回設計に使用したファイルを添付します。
Enter your E-mail address. We'll send you an e-mail with instructions to reset your password.



