Hi Community,
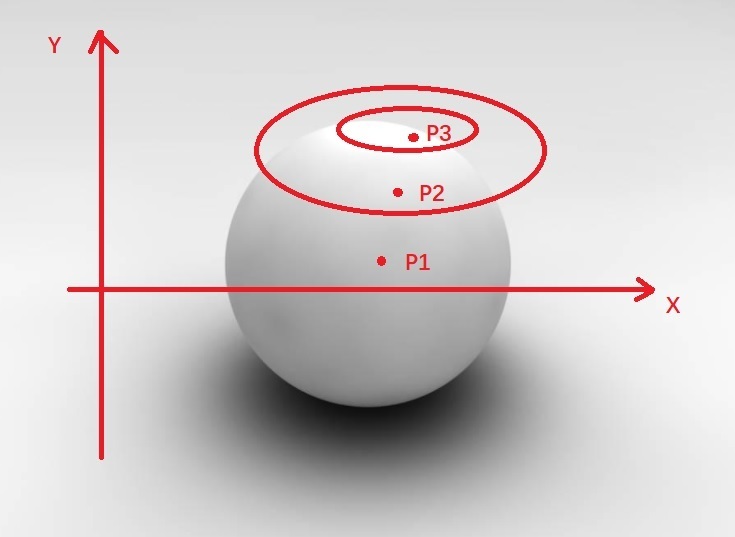
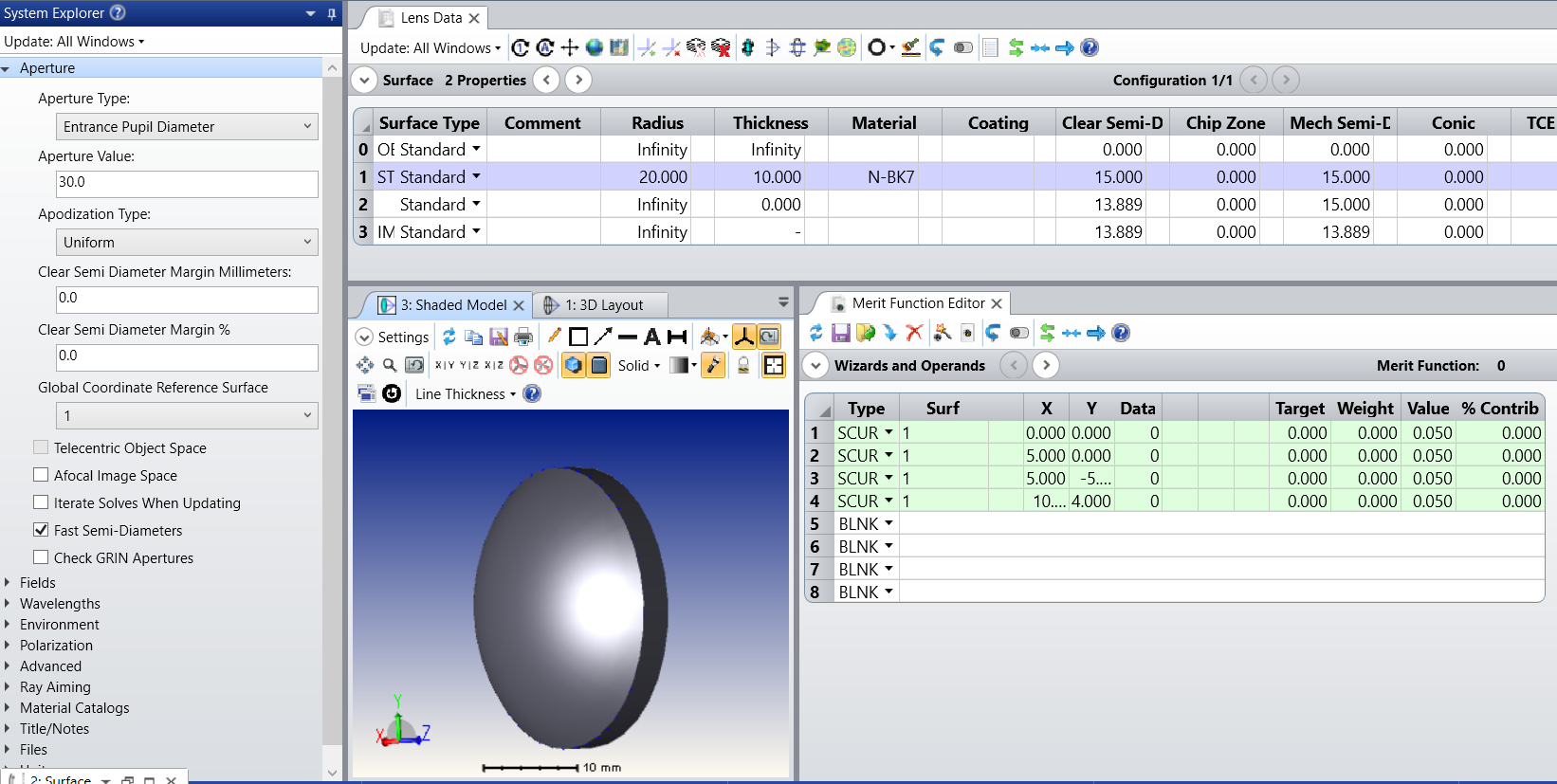
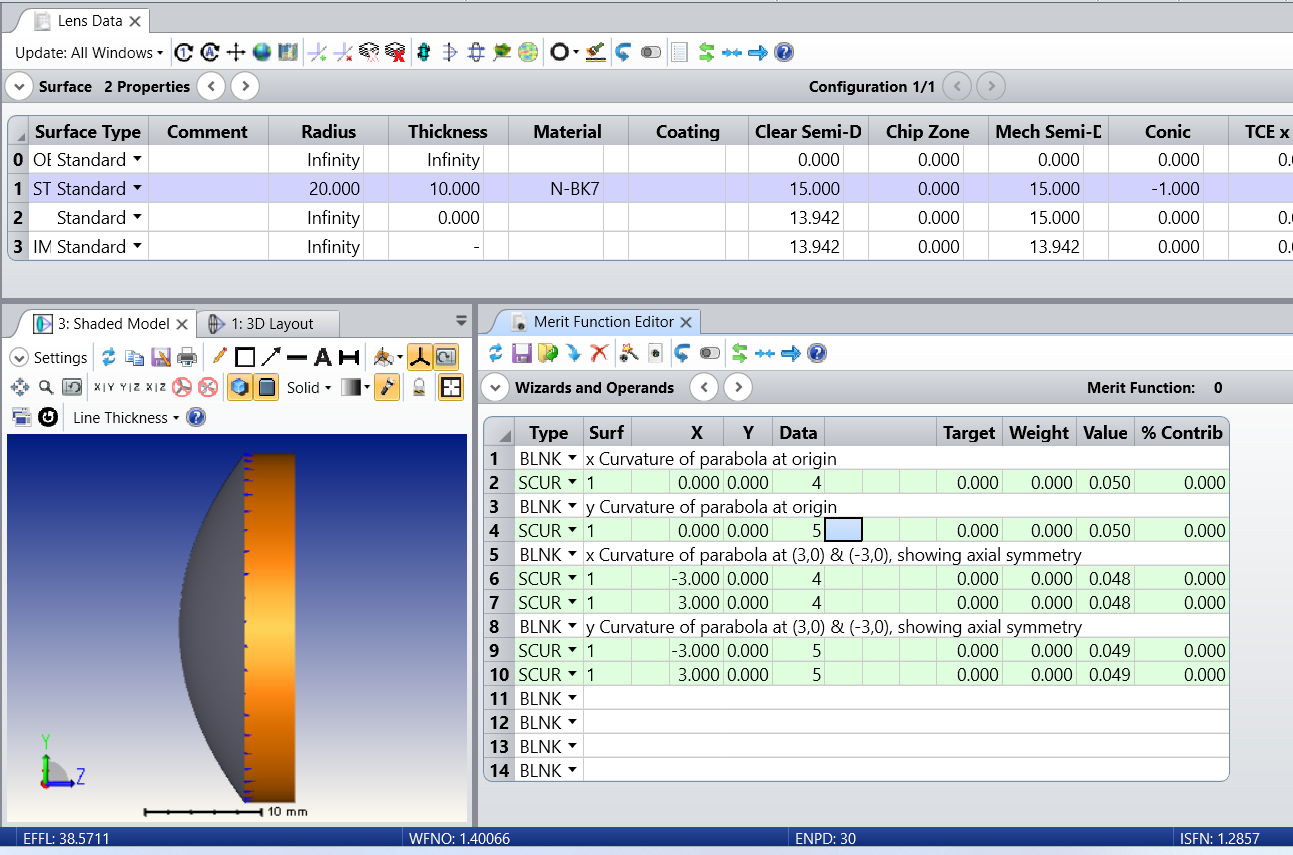
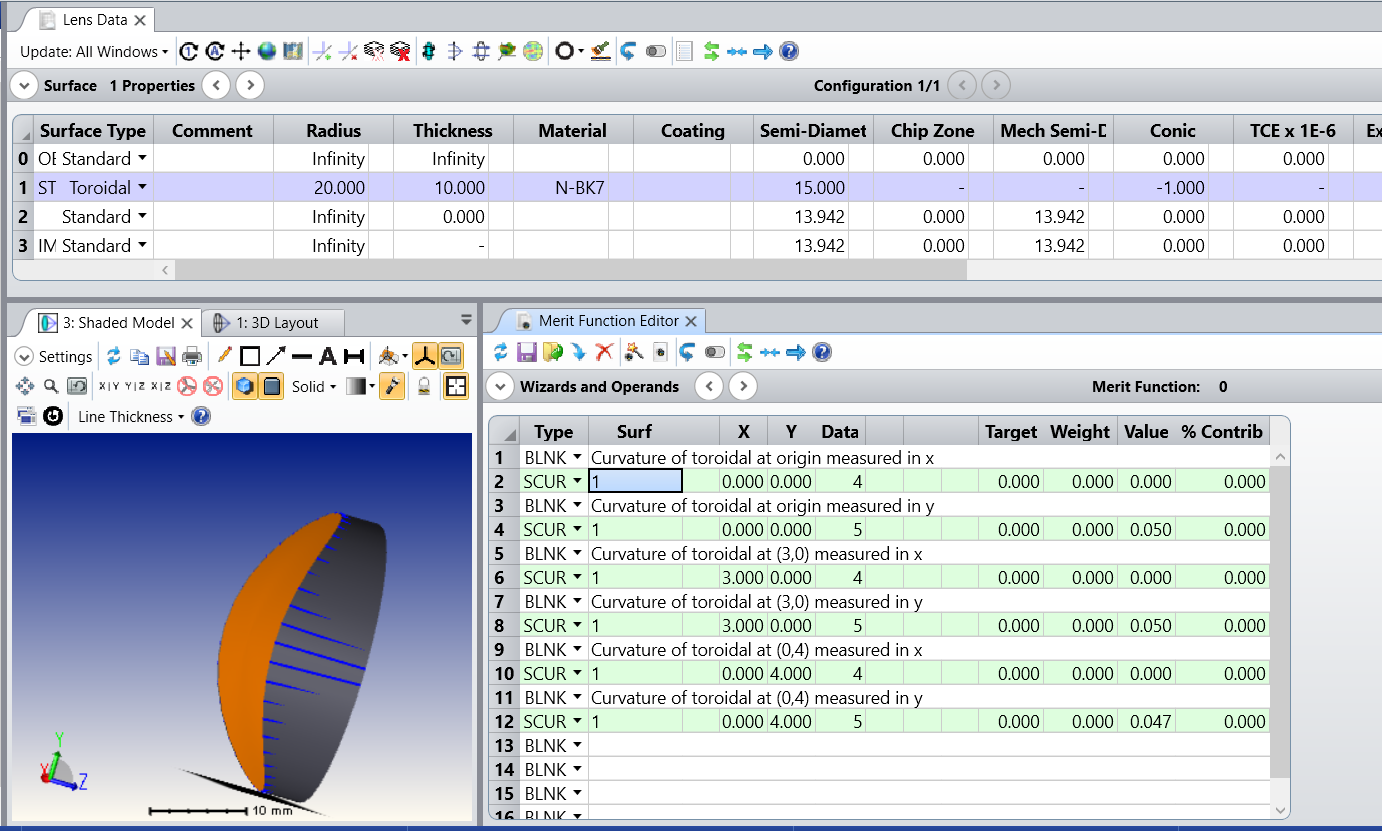
I am confused by the way Zemax calculate surface curvature in X and Y direction. Consider a very simple case: a sphere.Take latitude direction as X axis and longitude direction as Y axis, and pick up 3 points P1,P2,P3 in different latitude circle. You will see each latitude circle has different circular radius. SO I will expect surface cross section curvature analysis (or use SCUR operand for data 4/5) will give different curvature values in these positions,
BUT OpticsStudio always give same value constant equal to sphere curvature. Same true for use SCUR(data 4/5 for XY direction, even data 0/1 for tan/sag direction).
So what happened here? Did I miss something simple? thanks
Eric Yu