Hi Sepp,

Strictly speaking, if you have a mathematical expression for how the lenslets are distributed on the spherical surface, which isn’t obvious at all, you could use the ZOS-API or a macro to create the lenslets and position them accordingly. You could use spherical coordinates to locate the lenslet, but the question becomes: how to pick the sampling rate?

I made a simple dummy example:

1import numpy as np
2
3
4# Number of samples for theta and phi
5samp_t = 6
6samp_p = 15
7
8# Samples of theta and phi (using the physics convention: ISO 80000-2:2019 from Wikipedia on Spherical Coordinate System)
9theta_space = np.linspace(0, np.pi/8, samp_t)
10phi_space = np.linspace(0, 2*np.pi, samp_p, endpoint=False)
11
12# Spherical surface radius
13major_radius = 5.0
14
15# Standard lens type (used later in the loop)
16std_lens_type = TheSystem.NCE.GetObjectAt(1).GetObjectTypeSettings(ZOSAPI.Editors.NCE.ObjectType.StandardLens)
17
18# Default direction cosine for new objects stored as Vector A (used later in the loop)
19a_vec = np.array([0.0, 0.0, 1.0])
20
21# Loop over theta and phi
22for theta in theta_space:
23    for phi in phi_space:
24        # Calculate lenslet coordinates XYZ
25        x_pos = major_radius * np.cos(phi) * np.sin(theta)
26        y_pos = major_radius * np.sin(phi) * np.sin(theta)
27        z_pos = major_radius * np.cos(theta)
28
29        # Create new object (lenslet)
30        lenslet = TheSystem.NCE.InsertNewObjectAt(1)
31
32        # Change new object type to Standard Lens
33        lenslet.ChangeType(std_lens_type)
34
35        # Update new object XYZ position
36        lenslet.XPosition = x_pos
37        lenslet.YPosition = y_pos
38        lenslet.ZPosition = z_pos
39
40        # Update lenslet radius
41        lenslet.GetObjectCell(ZOSAPI.Editors.NCE.ObjectColumn.Par6).DoubleValue = -2.0
42
43        # There should only be a single lens at theta = 0.0 degree and it doesn't need a change of orientation
44        if theta == 0.0:
45            break
46
47        # Calculate direction cosine of the normal to the spherical surface at the XYZ coordinates
48        l_cos = x_pos / major_radius
49        m_cos = y_pos / major_radius
50        n_cos = z_pos / major_radius
51        norm = ( l_cos**2 + m_cos**2 + n_cos**2 )**0.5
52        l_cos /= norm
53        m_cos /= norm
54        n_cos /= norm
55
56        # The normal direction cosine is stored as Vector B
57        b_vec = np.array([l_cos, m_cos, n_cos])
58
59        # Using this thread: https://math.stackexchange.com/questions/180418/calculate-rotation-matrix-to-align-vector-a-to-vector-b-in-3d
60        # One can find the rotation matrix that aligns Vector A to Vector B
61        v_vec = np.cross(a_vec, b_vec)
62        c_val = np.dot(a_vec, b_vec)
63        v_x = np.array([[0.0, -v_vec[2], v_vec[1]], [v_vec[2], 0.0, -v_vec[0]], [-v_vec[1], v_vec[0], 0.0]])
64
65        # This is the rotation matrix
66        r_mat = np.identity(3) + v_x + np.dot(v_x, v_x) / ( 1 + c_val )
67
68        # Using this method: http://eecs.qmul.ac.uk/~gslabaugh/publications/euler.pdf
69        # One can decompose the rotation matrix into three rotations along the cardinal axes
70        # In our case, it is a little bit easier because the rotation about Z is the identity
71        # matrix (the lenslets are rotationally symmetric in this simple example).
72        # There is still an ambiguity (the rotation angle is an arccos of a matrix coefficient,
73        # therefore there is the plus and minus solutions that are valid), which is solved by
74        # looking at the lens XYZ coordinates
75        if x_pos < 0:
76            tay = -np.arccos( r_mat[0, 0] ) / np.pi * 180
77        else:
78            tay = np.arccos( r_mat[0, 0] ) / np.pi * 180
79
80        if y_pos > 0:
81            tax = -np.arccos( r_mat[1, 1] ) / np.pi * 180
82        else:
83            tax = np.arccos( r_mat[1, 1] ) / np.pi * 180
84
85        # Update the lenslet orientation
86        lenslet.TiltAboutX = tax
87        lenslet.TiltAboutY = tay

Which gives the following result:

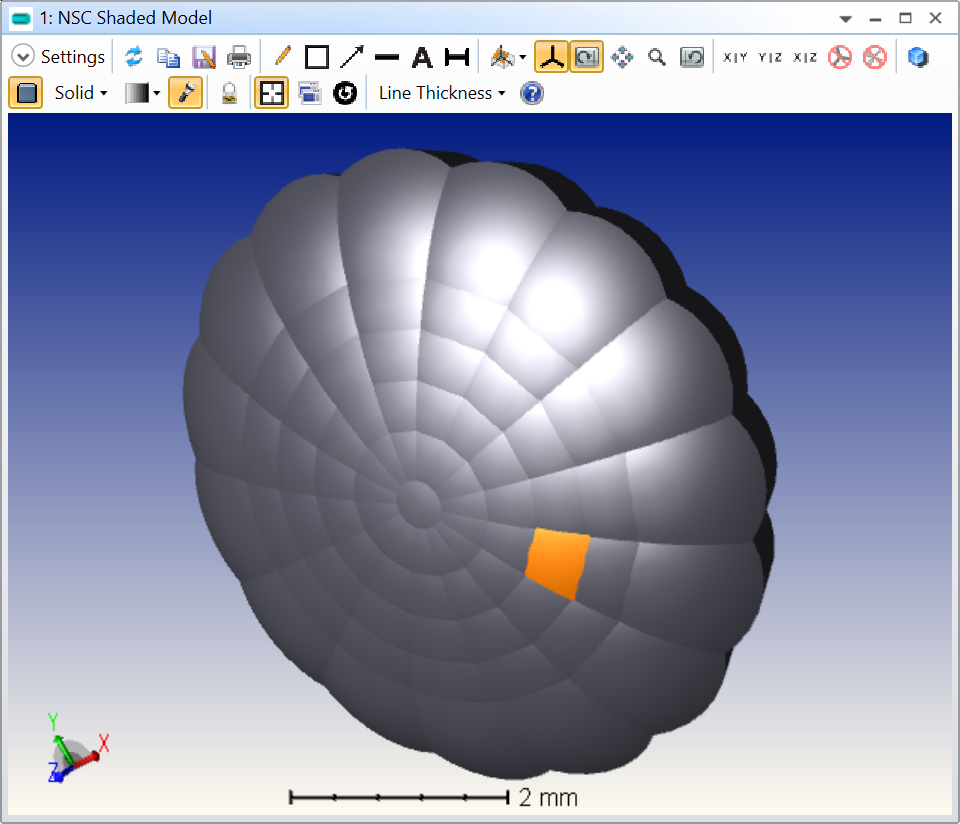
As you can see, using a uniform sampling leads to lenslet of different sizes and I don’t know how to solve that issue for your specific problem.

Alternatively, this array can probably be generated in a CAD software, and OpticStudio is able to import most of the CAD file formats.

Lastly, it might be worth clarifying what you are trying to achieve with this model. Can you consider a single lenslet at first? Are you interested in diffraction effects from the array?

Take care,

David