Dear Zemaxers, 

I have a question regarding the intensity distribution of a Gaussian at the stop aperture calculated by POP, versus the analytical solution of I(rho) = e^(-2*G*rho^2), where rho is the normalized radius coordinate. 
I have a stop aperture diameter of 6.0 mm, thus a radius of 3.0 mm.

The Gaussian beam has a waist size (i.e. radius) of 1.65822 mm. This gives me rho = 0.55274.

So, at rho = 0.55274 the intensity has dropped to 1/e^2. This leads me to calculate the apodization factor G:

G = 1/rho^2 = 3.27309

With this calculated apodization factor, I can calculate the intensity at the edge of the aperture (at rho = 1). 
I(rho = 1) = e^-(2*3.27309) = 1,43 *10^-3.

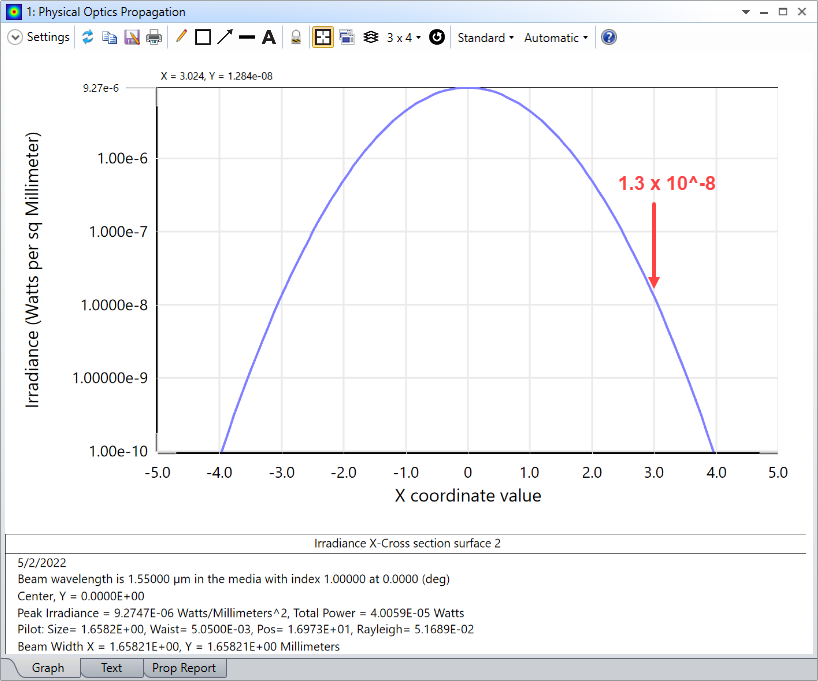
However, when I look at the intensity profile (cross-X display) calculated by POP I see that at r = 3.0 mm an intensity of  3.0*10^-4. 

Where does this deviation come from?

See also the image attached:

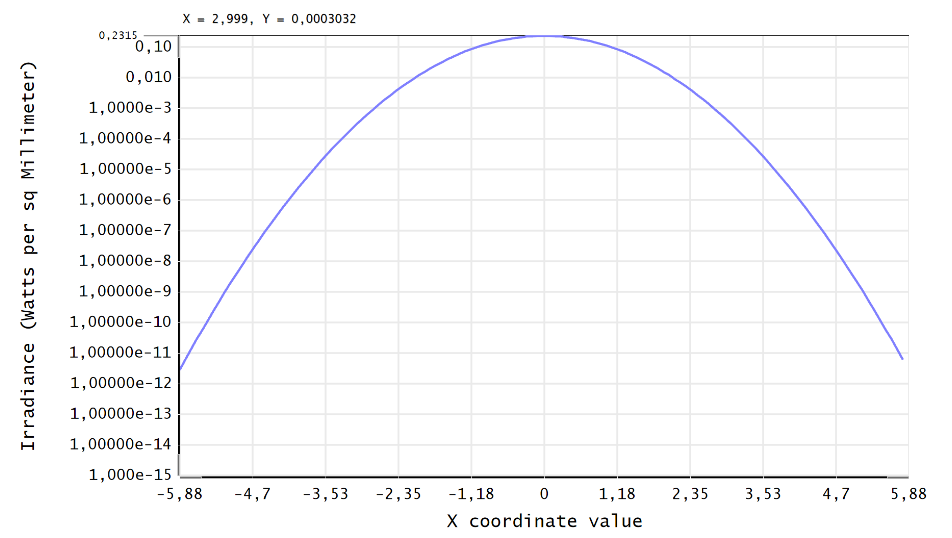
Note that beam size of the pilot beam at surface 2 (that is the stop aperture of diameter 6.0 mm) is 1,6582 mm. 
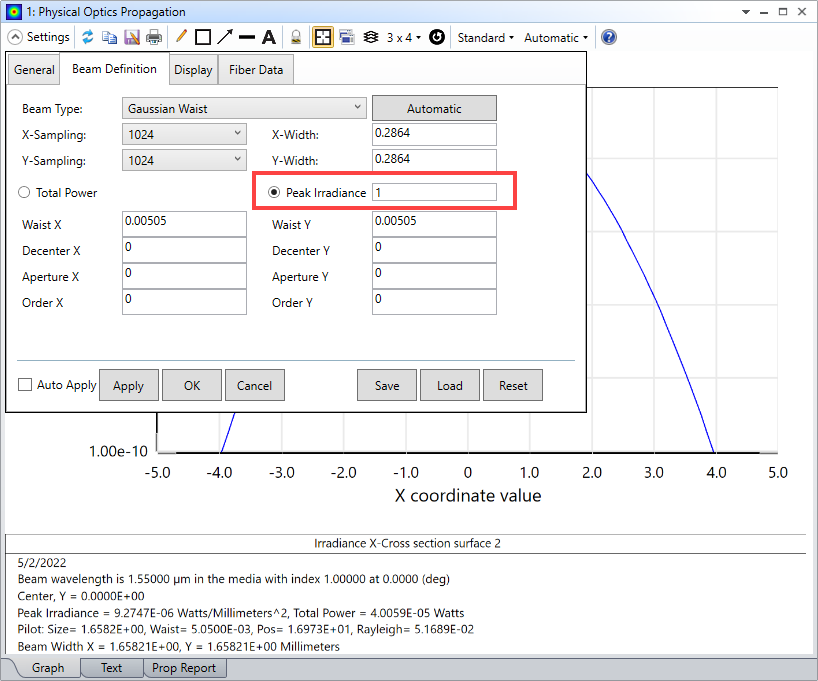
I sampled with 1024x1024. See the POP settings:
 

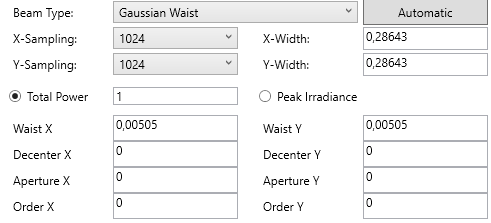
Finally, I present a screen shot of the lens data editor

 
Could someone explain where the difference come from of the intensity value at the edge calculated via POP, and the analytical solution of I(rho) = e^(-2*G*rho^2)?

Thank you very much! Any help is much appreciated.