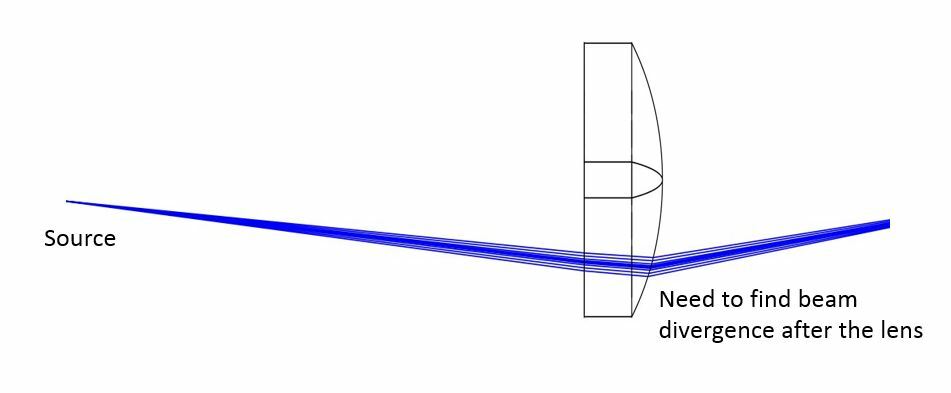
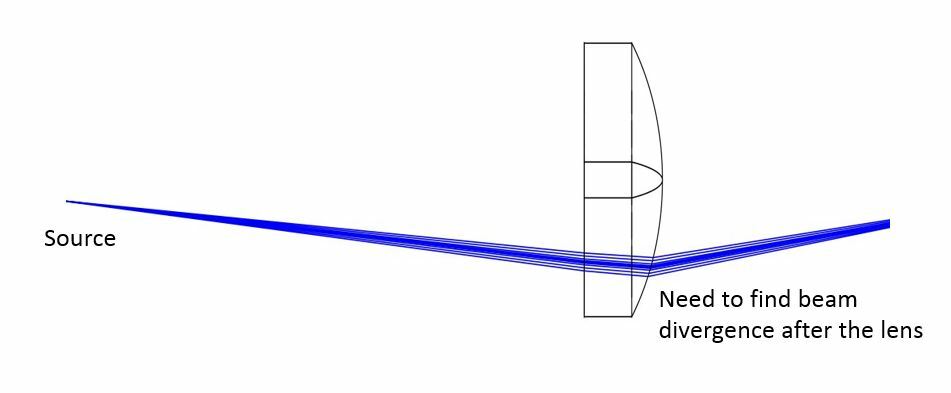
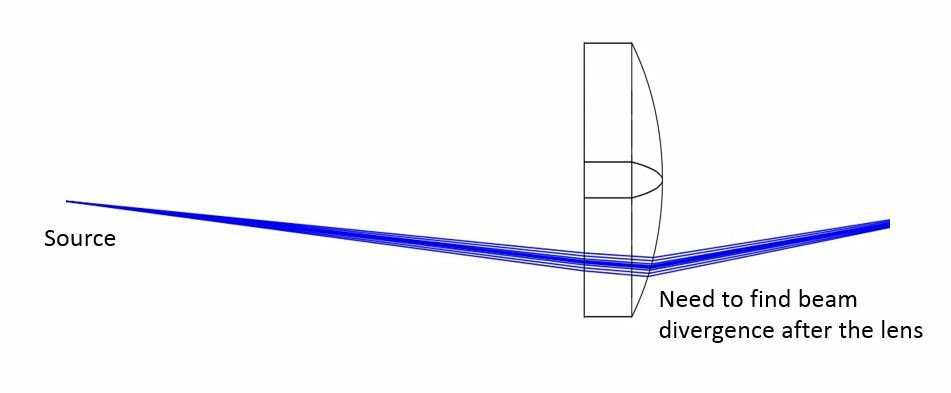
In the Physical Optics Propagation, how can I compute the divergence of the beam ? Is there a POPD operand data?
Best answer by David Nguyen
View original
In Physical Optics Propagation, the divergence angle cannot be directly returned with a POPD operand data.
The recommended workaround for this is to insert 2 dummy surfaces at different distances, look at their beam size r1 and r2, then calculate the divergence angle based on the beam size variation as it propagates. To compute the beam size using Physical Optics Propagation, the operand is POPD, and the data type is 23 and 24 for beam width along the X and Y directions, respectively.
For a rotationally symmetric system, you only need to use one of them.
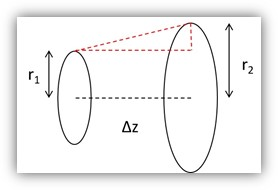
Using POPD 23, you can get the beam radius at the first surface r1 and the bream radius at the second surface r2. If the 2 surfaces you measured the beam radius at are separated by Δz, then you can use the following equation to calculate the divergence:
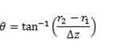
If you know the Δz separation, you can simply use the following operands:
- POPD (beam size)
- GLCZ (z position of surfaces)
- DIFF (subtract 2 operands)
- DIVI (divide 2 operands)
- ATAN (arctangent of operand)
The merit function to compute this divergence angle between surface 6 & 7 could be similar to this:
I think that the issue is that for a generalized beam, 'divergence angle' is not a well defined concept.
For a pure Gaussian beam, you can characterize the beam with just wavelength, beam waist and beam divergence. If you are many Rayleigh ranges away from the waist, you can pretty much ignore the beam waist itself and just scale the beam size at any two positions outside of the RR using the divergence angle, which acts effectively like a cone angle.
When the beam is more complex than a pure Gaussian, Siegman introduced the M^2 number to define 'how much faster than a pure Gaussian' the real beam expands. Many RRs out from the waist, where we can neglect the waist size itself, you can consider the 'effective divergence' to be just M2*pure Gaussian divergence. But for propagation from some arbitrary position, to another arbitrary position, there is no concept of divergence that acts as a simple scalar. That's why POPD does not report beam divergence: there really is no such property of the beam.
Dear all,
Is there any way to find the beam divergence after the lens. Response will be appriciable and I will be very thankful to you
I am using a beam (Not gaussian beam or POP) incident at some angle on the lens and I need to know the beam divergence after the lens.
Reagrds,
Faheem
Hi Faheem
To measure a beam divergence, I think one easy way is to tick 'Afocal Image Space' under the System Explorer > Aperture. Then when you open a spot diagram, the units will be in angle.
Sandrine
Thank you so much for your kindness. It is working well thank you very much.
I have following doubts
(1) How it is calculating the divergence?
(2) Is there anyway to make the beam collimated after the lens shownas shown in the attached image?
I will be very thankful to you.
(3) Another question is that, whether this way which you have suggested to find the beam divergence will work to find on the rear surface of the lens?
Thanks and Regards,
Faheem
Reply
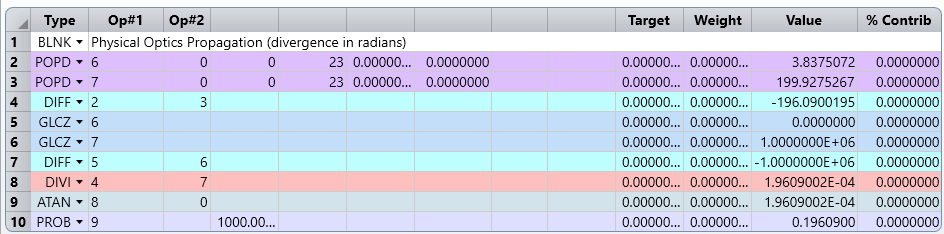
Enter your username or e-mail address. We'll send you an e-mail with instructions to reset your password.
Need more help?
To Chinese users:
Do not provide any information or data that is restricted by applicable law, including by the People’s Republic of China’s Cybersecurity and Data Security Laws ( e.g., Important Data, National Core Data, etc.).
不要提供任何受适用法律，包括中华人民共和国的网络安全和数据安全法限制的信息或数据（如重要数据、国家核心数据等）。