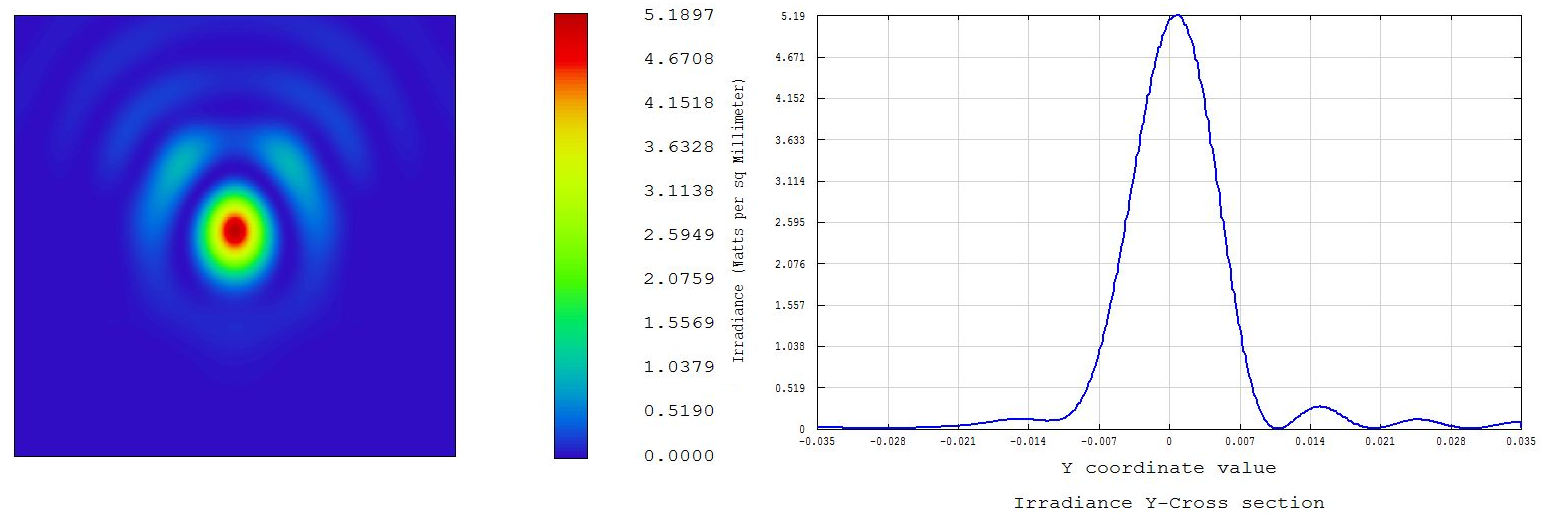
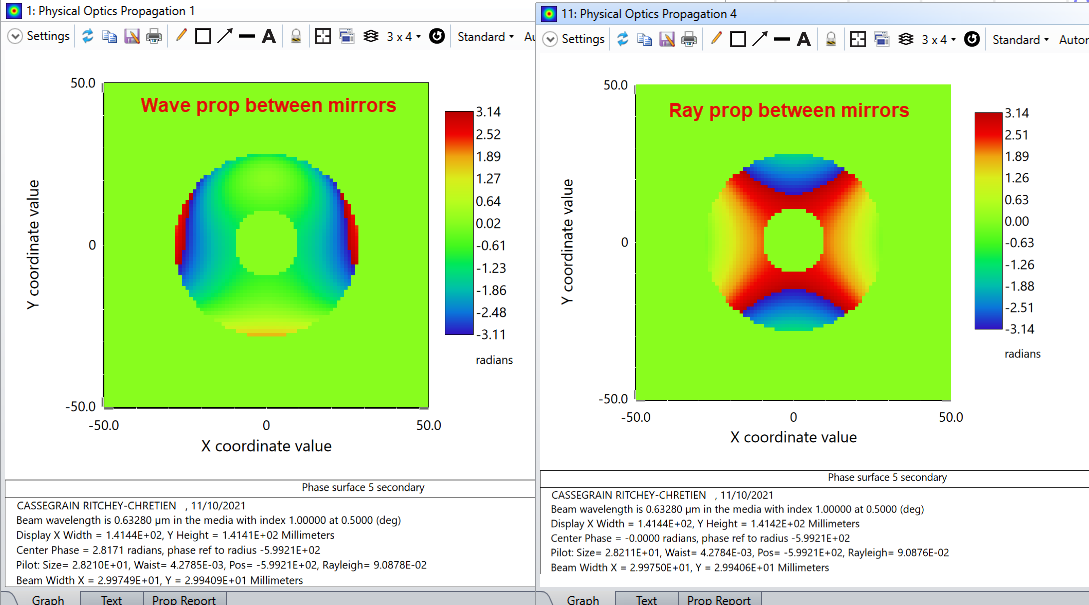
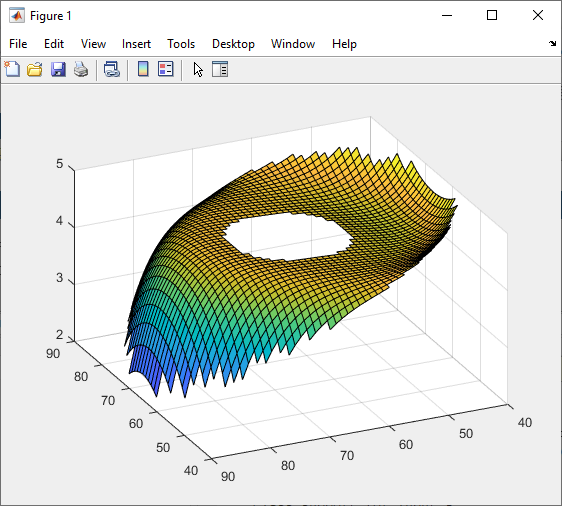
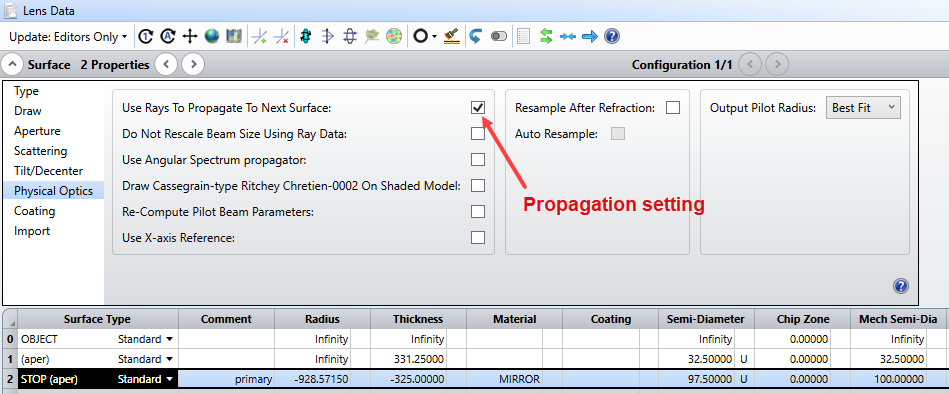
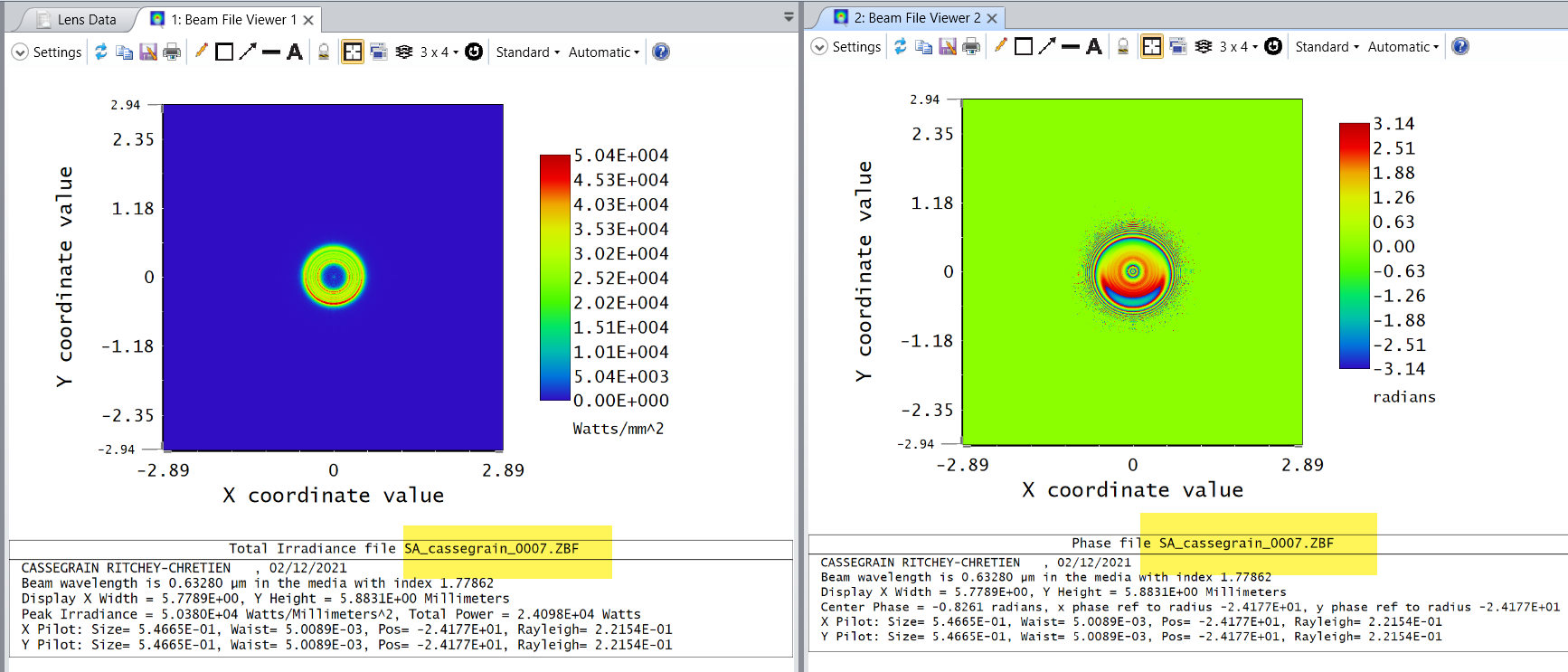
Hi, I followed the recommendations given in other forum threads (ref. 1) or tutorials from Zemax. My optical model consists of a standard Ritchey-Chretien telescope such as f#=6 and fl~500 [mm]. However the PSF obtained using the "Huygens" method (as it is a non sequential system) and POP are quite different. In both cases, the illumination of the entrance pupil is uniform (="Top Flat Apodization"). In addition, I don't see any artifacts in both results that would point to a "bad choice of algorithm" or settings (e.g. under-sampling). Below, please find attached, the spot diagram, the diffraction pattern calculated with the "Huygens" method, and the one calculated by POP, for the outermost position in the FOV (but this is also true for intermediate positions in the FOV). Do you have any comments to explain this discrepancy? Thank you for your help.
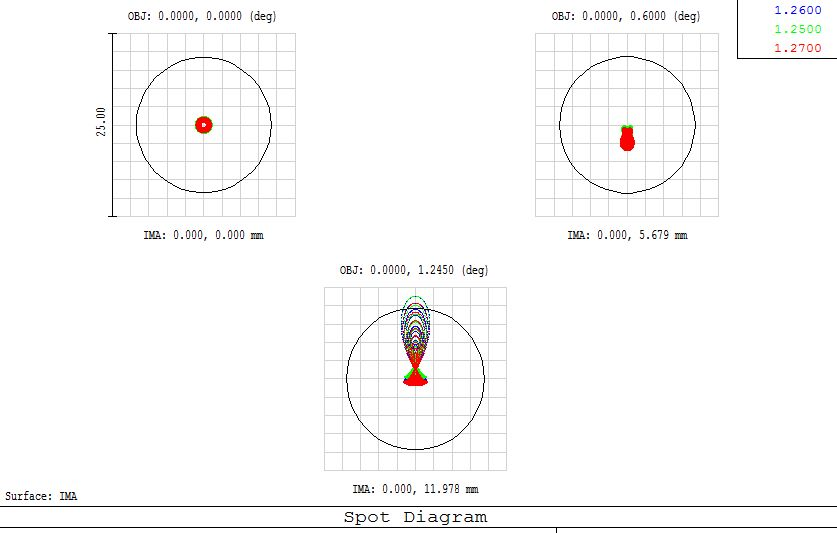
SPOT DIAGRAM:
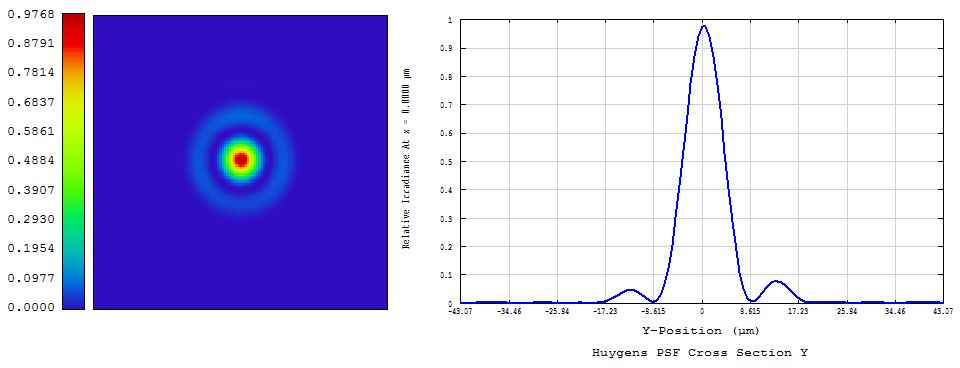
“Huygens” DIFFRACTION PATTERN:
“POP” DIFFRACTION PATTERN: