角スペクトル伝搬の理論的導出

角スペクトル伝搬は、平面波の伝搬について議論します。z＝０の位置とz＝Zの位置に平面の射出面と測定面を考え、測定面の電場の複素振幅が分かっているときに、測定面での電場の複素振幅を求めます。（図１）
 

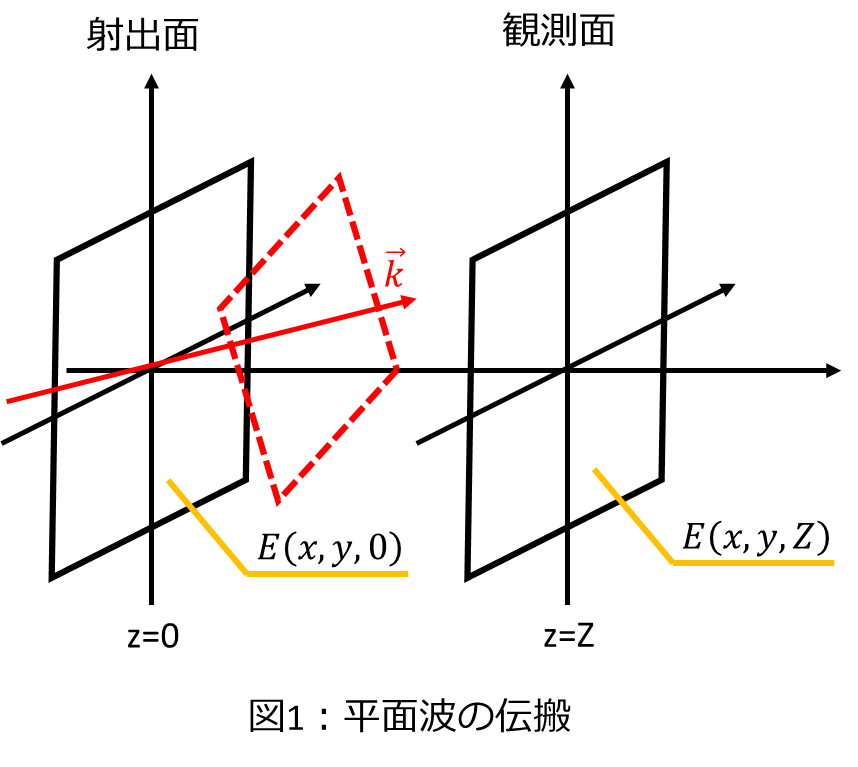
任意のkベクトルの平面波は方向余弦α、β、γと位置ベクトルrを用いて以下の式で表すことができます。
 

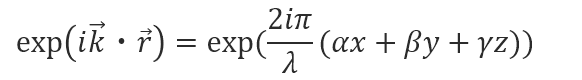
これが、平面波の伝搬方程式です。
この式のα、β、γはx,y,zの方向余弦を表しており、以下のような関係になります。
 

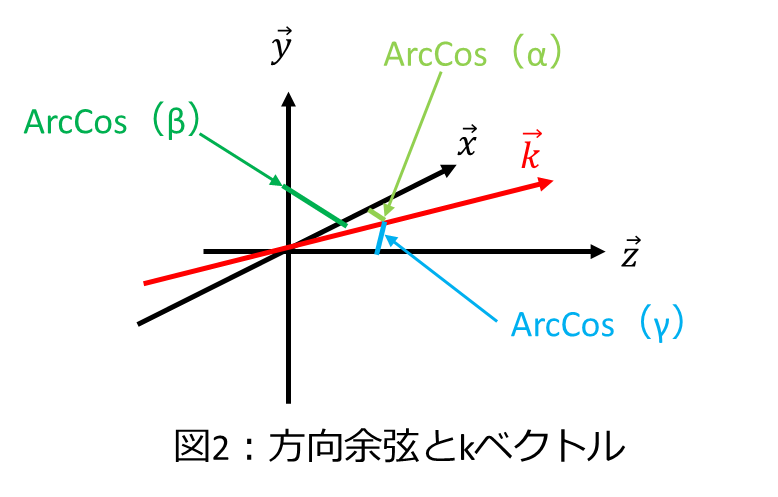
次にフーリエ変換とフーリエ逆変換を以下の様に定義します。
 

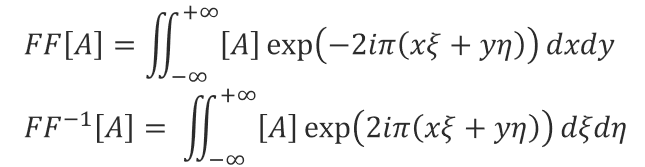
平面波の式に対して、以下の変換をして考えてみます
 

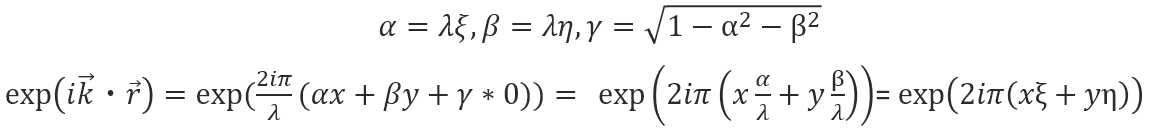
ここで、z=0の位置の電場をフーリエ変換したと考えて、その関数をG(x,y,0)とします。
E(x,y,0)は、

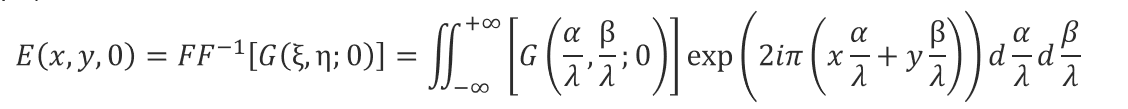
が成り立ちます。
この式の物理的な意味は、z=0の電場は、無数のαとβによってあらわされるG(x,y,0)というスペクトル分布を持つ、様々な方向の平面波のz=0の位置での集合であるということになります。これが角スペクトルの意味です。

Zだけ進んだ位置での電場E(x,y,z=Z)の計算に、角スペクトル空間を用います。

電場E(x,y,z=Z)をフーリエ変換した、G(ξ,η;Z)を考えます。

すると、E(x,y,Z)はG(ξ,η;Z)のフーリエ逆変換として、
 

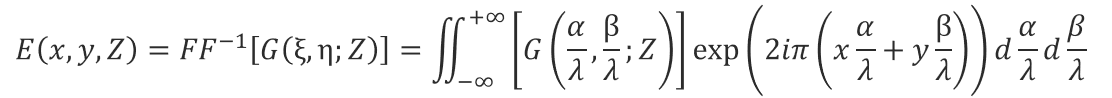
となります。電場は光源でない空間でのヘルムホルツ方程式に従うので、Zを変数として代入します。

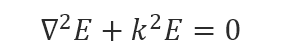
フーリエ逆変換の式から、Ｅの式にはxとyは平面波の項にしか含まれないので以下の簡単な形に書き換えられます。
 

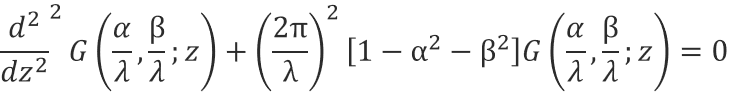
この微分方程式の基本解は以下の様に書くことができます。

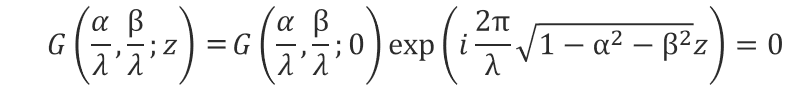
ここで、OpticStudioの物理光学伝搬ではkベクトルがZ軸に対して大きな角度をとらないという以下の近似を行います。
 

結果、上記の式は以下の様に整理されます。

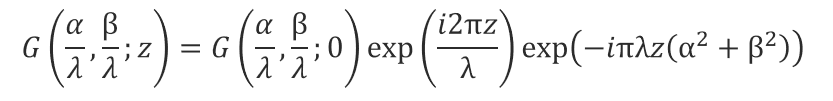
exp⁡(i2πz/λ)の項は面全体の位相の増加分を表しています。今計算において、面全体の絶対位相を知りたいのではなく、相対的な電場の複素振幅の分布を知りたいはずです。そのためこの項は無視できます。

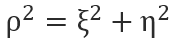
とすると、

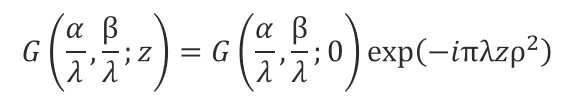
を導けます。最終的にこの値の逆フーリエ変換が求めるE(x,y,z)となります。

ここまでを整理して、PTP(Plan to Plan)演算子として以下を定式化します。

角スペクトル伝搬の注意点
 

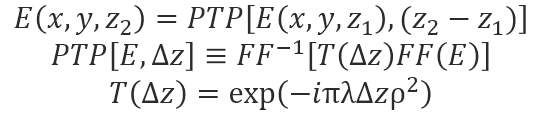
伝達関数 T(Δz) は、振幅は 1 ですが、位相を持つ複素数です。
この位相は、λΔzρ2 が小さい場合、周波数領域表現 G の各点の間でゆっくりと変化しますが、λΔzρ2 が大きくなると、位相は急激に変化するようになります。

有限な配列の中で隣接する 2 点の間での位相変化が、およそπ/2を超えると、位相は不明確になり、エイリアシングと呼ばれる現象が発生します。

このため、角スペクトル計算手法は、伝播距離が比較的短い場合またはビームがほぼ平行である場合に良好に機能します。

角スペクトル伝播を使用する場合、電界の位相は平面を基準にして測定されます。正の位相は、伝播方向とは関係なく、この平面から見てローカル座標の+z 軸方向に波面が進んでいることを示しています。

原則として、ビームのサイズが著しく変化しない場合は、角スペクトル プロパゲータを使用できます。フレネル数が小さくてビームのサイズが著しく変化するビームの伝播では、別の理論と数値手法が必要になります。