偶数次非球面のサグ量は、以下の式で表されます。

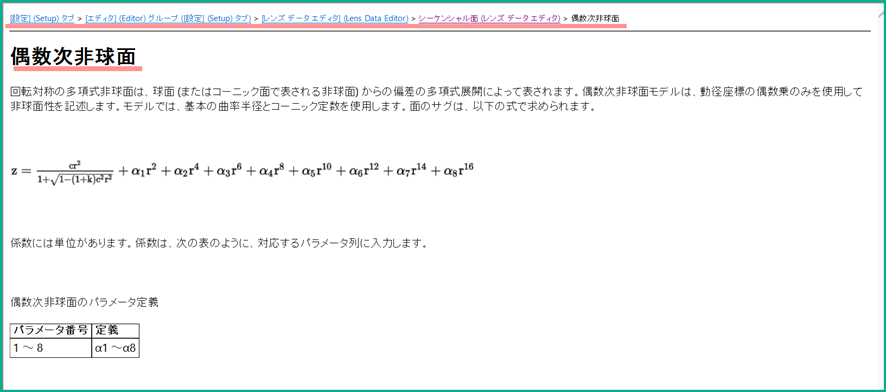
一方、長さに関連するパラメータは以下の様に、熱膨張も加味されることがかかれています。

これらはどのようにつながるのかを、解説します。

サグ量の式では、Zは長さの次元を持ちます。そして、rも長さの次元を持っていますので、このことから、α1~α8はそれぞれ[長さ]-1~[長さ]-15の次元を持っていることが分かります。

この長さが、TCE×ΔTだけ伸びたとして計算します。

以下例題を用いて計算してみます。

以下の様にTCE=8、曲率半径100、α1～α3の値＝100とした偶数次非球面を第2面に設定したモデルを作成しました。

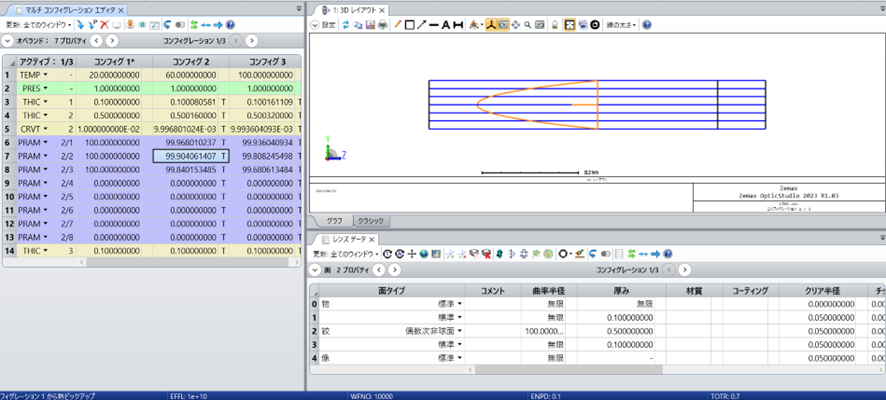
各コンフィグレーションの温度は、20℃、60℃、100℃となり、それぞれのコンフィグの温度差は、コンフィグ2では40℃、コンフィグ3では80℃となります。

この時、コンフィグレーション2に対する、長さは1+8*10^-6*40=1.000032となります。

そのため、曲率半径は100*1.000032=100.0032

この逆数である曲率は、1/100.0032=9.9968010237E-03

α1は、100/1.000032=99.968010237

α2は、100/((1.000032)^3)= 99.904061407

α3は、100/((1.000032)^5)= 99.840153485

となります。

同様に、コンフィグレーション3では

この時、コンフィグレーション2に対する、長さは1+8*10^-6*80=1.000064となり、

曲率半径は100*1.000064=100.0064

この逆数である曲率は、1/100.0064=9.9936040934E-03

α1は、100/1.000064=99.936040934

α2は、100/((1.000064)^3)= 99.808245498

α3は、100/((1.000064)^5)= 99.680613484

となります。

このように、熱解析時に設定されるパラメータの計算は行われます。