フレネル回折伝搬の理論的解説 

フレネル回折伝搬は、図1のようなx1,y1,z1座標系の平面開口からZ離れた距離のx2,y2,z2座標系の観測面にに対する球面波の複合として計算します。

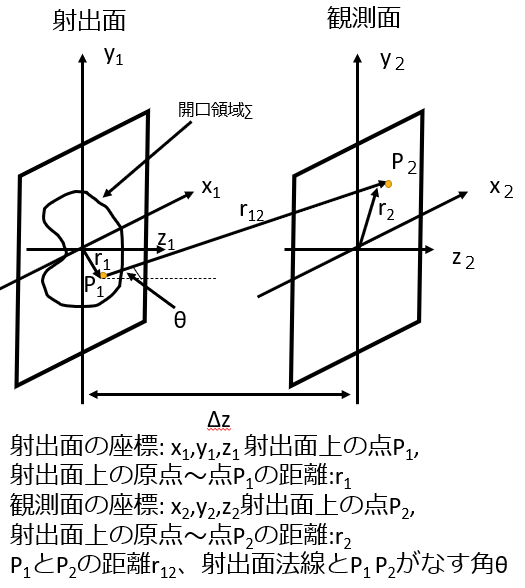
図１：フレネル回折伝搬のイメージ図

まず、平面開口の伝搬を示す以下のレーリーゾンマーフェルト回折公式から出発します。なお、kは波数で2π/λです。

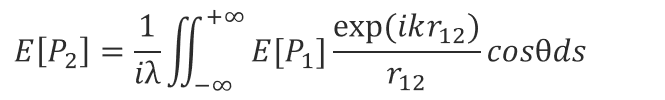
ここでcosθ=Δz/r12  なので、

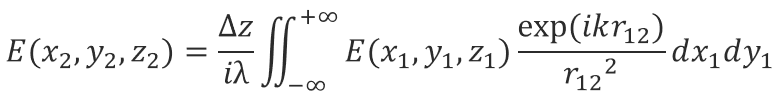
と書けます。

ここで、距離r12について考えます。この距離は図１から以下の様に求めることができます。

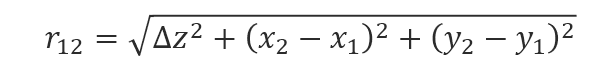
OpticStudioのPOPの前提条件については、以下の制約があります。

この制約をもとにした近似をフレネル近似といいます。

このことから上記のr12の式に対して、指数関数の中では以下の様に第2項まで展開し近似値として使用し、
 

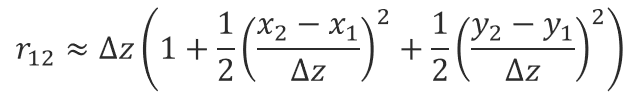
分母で用いられている r12はΔzとして近似します。

この近似を先ほどの電場の式に当てはめることで、
 

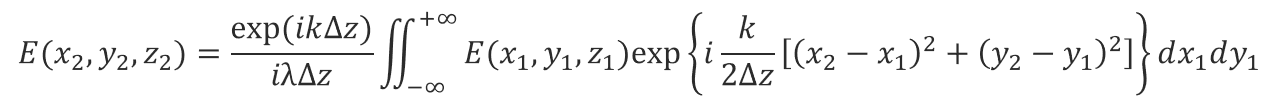
となります。

この式をdx1,dy1に注目してなおかつフーリエ変換を意識してｋを一部分解して整理することで、以下の様にヘルプファイルと同様の式を得ることができます。

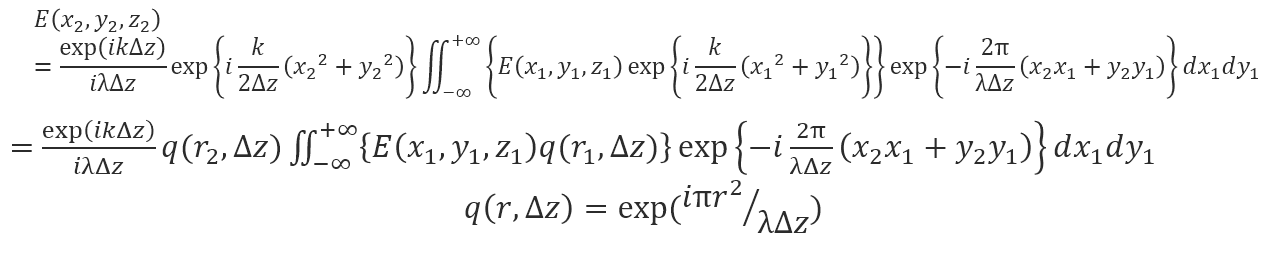
この式から、3つの重要な意味が読み取れます。

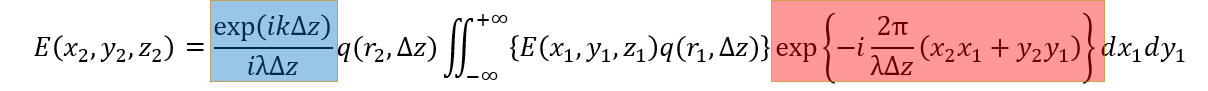
1つ目は青いエリアの第１項です。この意味は以下の通りです。

２つ目は赤いエリアのフーリエ変換部です。

これは射出面での電場の位相と強度が分かればΔz離れた観測面での電場の位相と強度の分布はフーリエ変換すれば求まることを示しています。

3つめは２つのqの式です。この意味は以下になります。

このことから、なぜPOPに使用できる面や機能に制限があるのかも理解できます。
例えばNSCモードでは複数光源や複数像面を設定できますが、各光源や光路の面までのビームウェスト距離が異なると上記の計算がうまくいかなくなるめですし、ブラックボックスレンズ面では電場を計算されるための各面によって発生する電場の位相の情報を正確に計算できないためです。