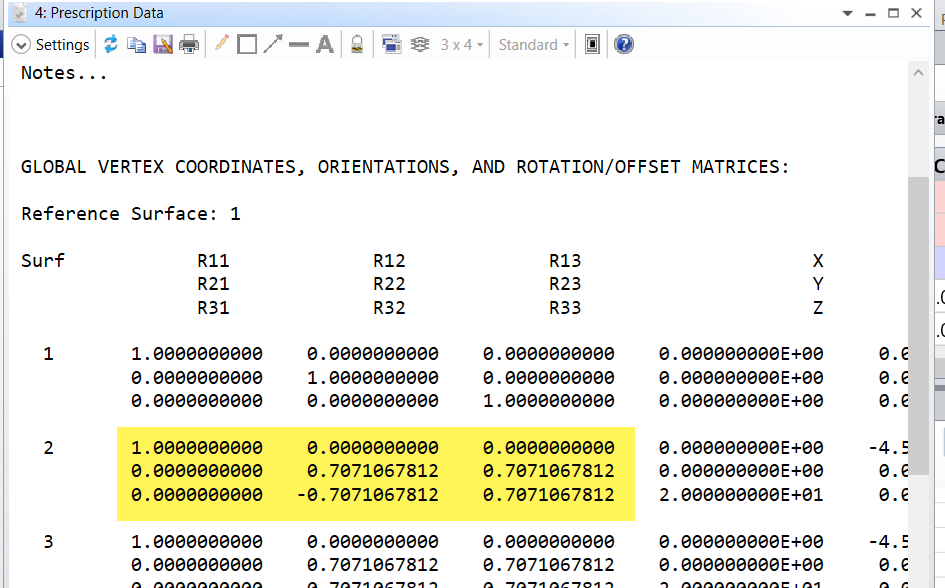
https://support.zemax.com/hc/en-us/articles/1500005576822-Rotation-Matrix-and-Tilt-About-X-Y-Z-in-OpticStudio is misleading.
OpticStudio uses degrees for Tilt About X/Y/Z, and this graphic suggests using theta_x = tilt about x. Tilt about X is in degrees, but theta_x should be in radians. If you do as the graphic suggests and plug in degrees, you'll get the wrong rotation matrix.
Please let me know if I'm wrong here.
Question
Problem with rotation matrix article
Enter your E-mail address. We'll send you an e-mail with instructions to reset your password.