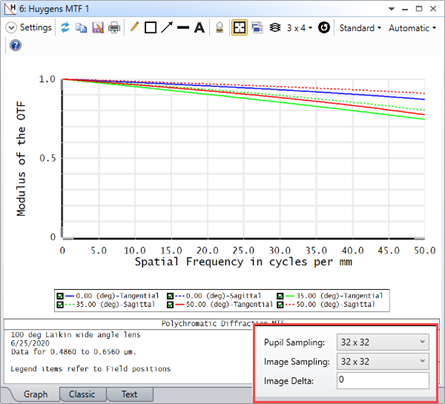
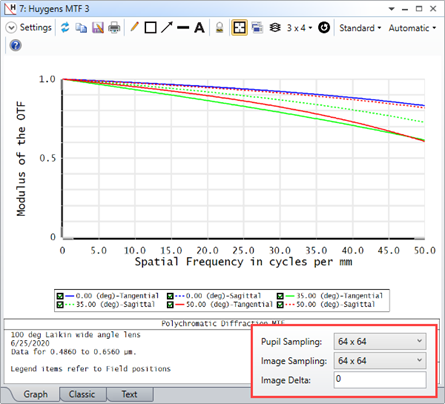
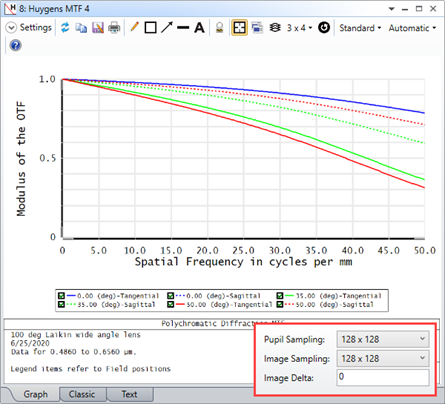
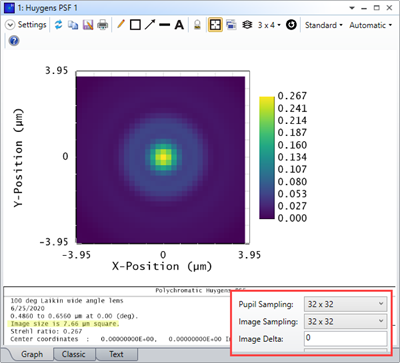
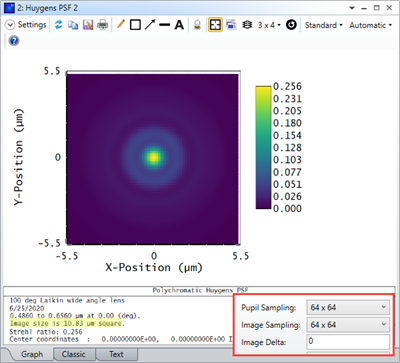
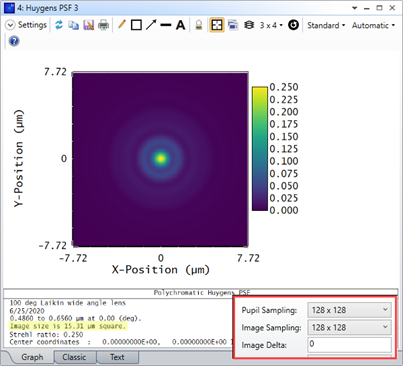
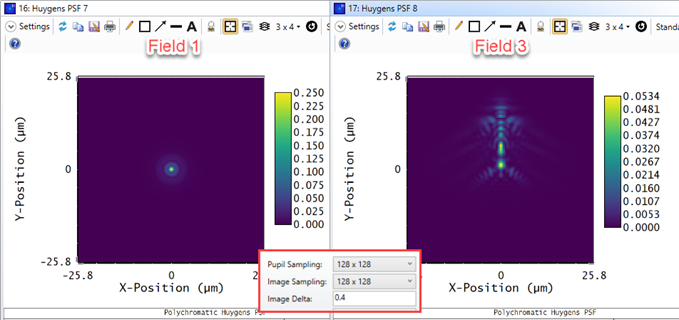
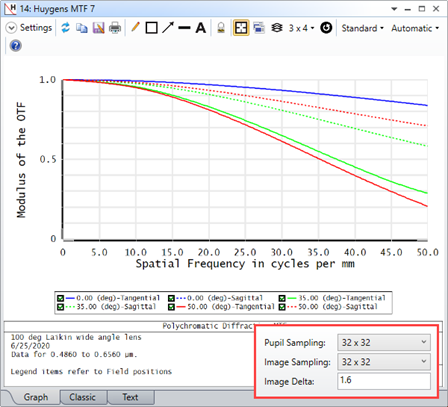
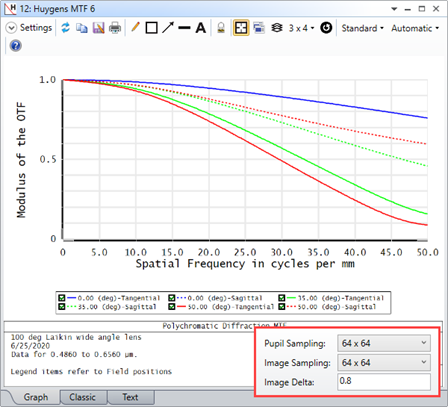
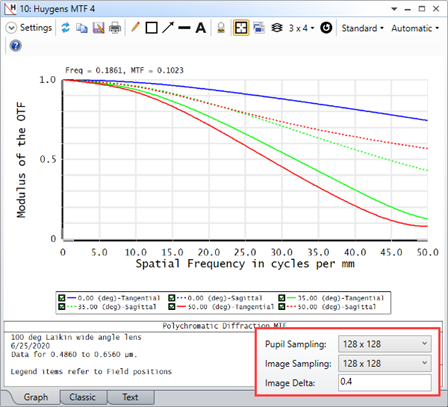
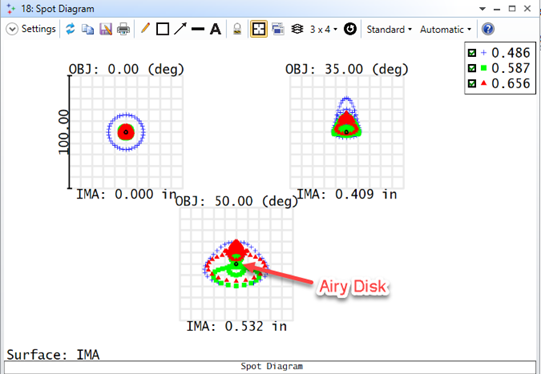
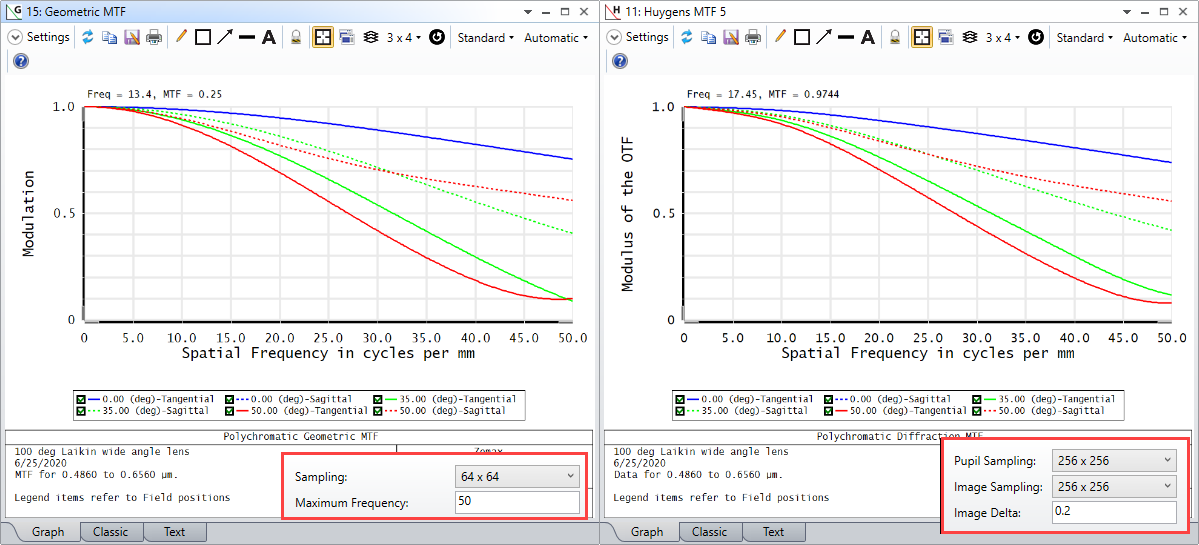
For some systems, when I increase the Pupil and Image Sampling for my systems, I don't see a convergence in results. Rather, it looks like the results become more divergent as I increase my sampling. Why is this?
Enter your E-mail address. We'll send you an e-mail with instructions to reset your password.