Generating the Qcon polynomials
OpticStudio supports Q-type aspheres. Type 0 indicates Qbfs polynomials, and Type 1 indicates Qcon polynomials. The functional forms of the Q-type polynomials are fairly complex due to the requirement that the polynomials be orthonormal for a circular aperture. Occasionally, it is convenient to know the functional form of the polynomials for testing and comparison purposes.
Below, we list the first 20 Qcon polynomials, and also share the derivation in the Mathematica file GenerateQConPolynomials.nb. The .nb files for Mathematica can be used by downloading the free Wolfram Player: https://www.wolfram.com/player/.
Important equations for the Qcon polynomials
The Qcon polynomials can be calculated in a straightforward way using an equation for the Jacobi polynomials.
From Shape specification for axially symmetric optical surfaces, G.W. Forbes, Optics Express 5218, Vol. 15, No. 8, 16 Apr 2007, the polynomials are related to the Jacobi by:

And Wikipedia (https://en.wikipedia.org/wiki/Jacobi_polynomials) lists the special case of the Jacobi polynomials for all positive integers:

Calculating the Qcon polynomials
The attached Mathematica file, GenerateQConPolynomials.nb, can be used to calculate any of the Qcon polynomials. The .nb files for Mathematica can be used by downloading the free Wolfram Player: https://www.wolfram.com/player/.

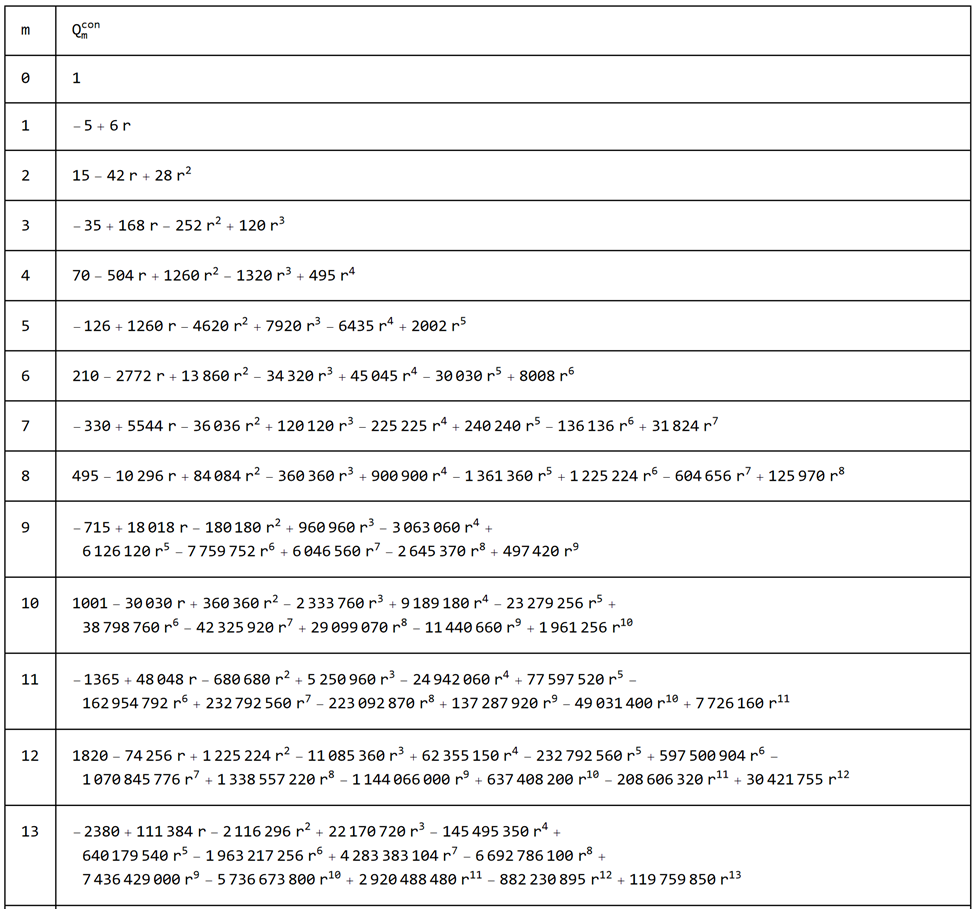
Listing of the Qcon polynomials
The first 20 Qcon polynomials are listed below.