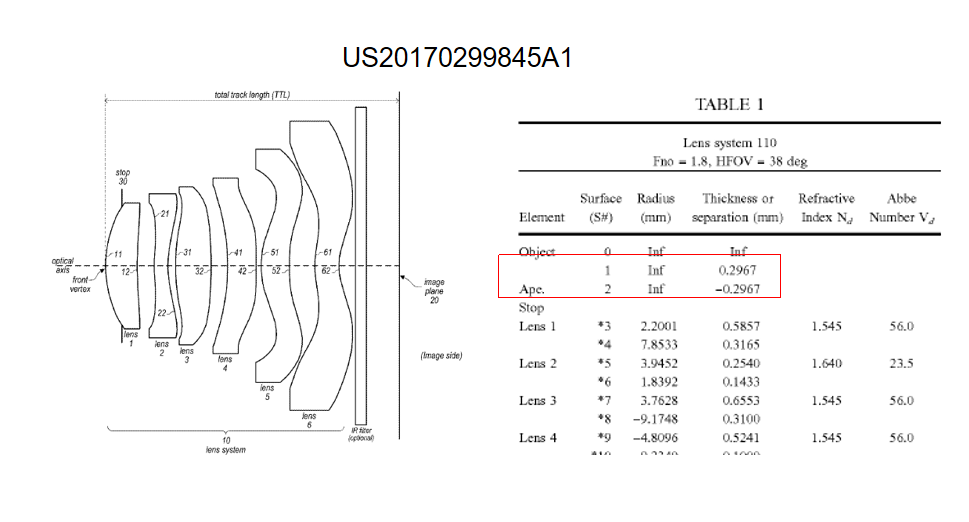
An interesting problem has surfaced as the Zemax team at Ansys continues to develop toolsets to aid the simulation of small form-factor, wide-angle systems such as cellphone camera lenses. Different ways exist to set up and model a stop with a lens traversing its aperture, but which is the best way? With this post, we share our recommendations and seek your feedback based on your experiences tackling this challenge.
Virtual propagation modeling is one of the ways to model these stops. Technically, the portion of the lens that goes through the stop will modify the wavefront before the stop limits the wavefront with its clear aperture. Therefore, we cannot use virtual propagation to model these stops because we will be adding non-real pupil aberrations to our optical systems since we are forcing the entrance pupil to be flat when it is not.
Here is an example of a stop with a lens going through it.
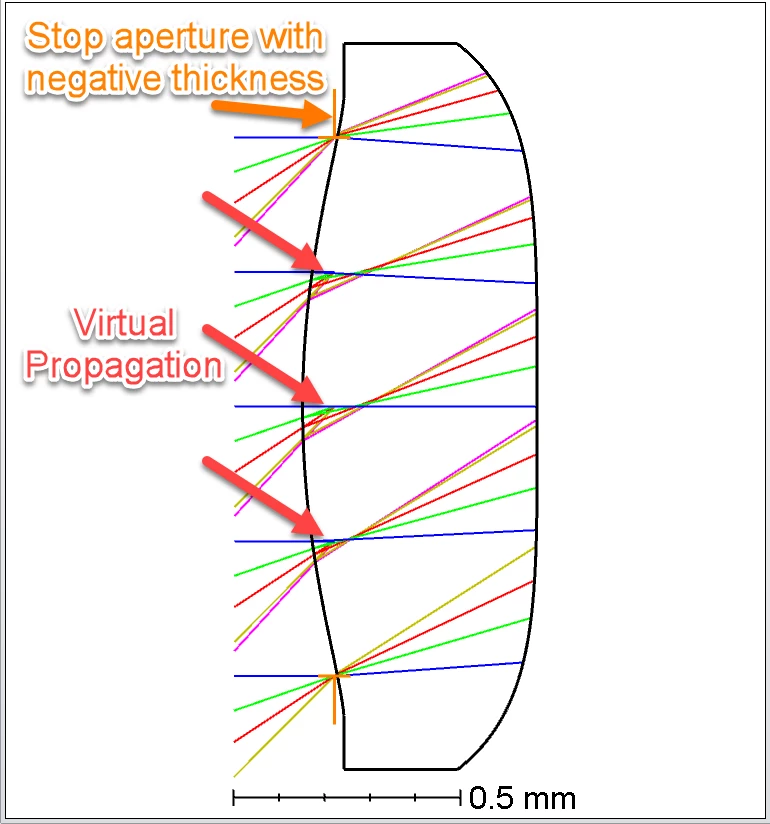
By definition, “the aperture stop is the aperture in the system that limits the bundle of light that propagates through the system from the axial object point. The stop can be one of the lens apertures or a separate aperture placed in the system. However, the stop is always a physical surface.” (Field guide to geometrical optics, J. E. Greivenkamp).
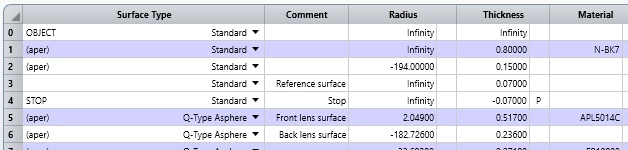
Therefore, a team of Zemax Engineers at Ansys has studied the effects of modeling the stop in different ways and concluded that the best way to model these systems is by separating the lens into two: the first section that goes through the stop and the section that does not go through the stop. These “two” lenses will embed the stop as shown below.
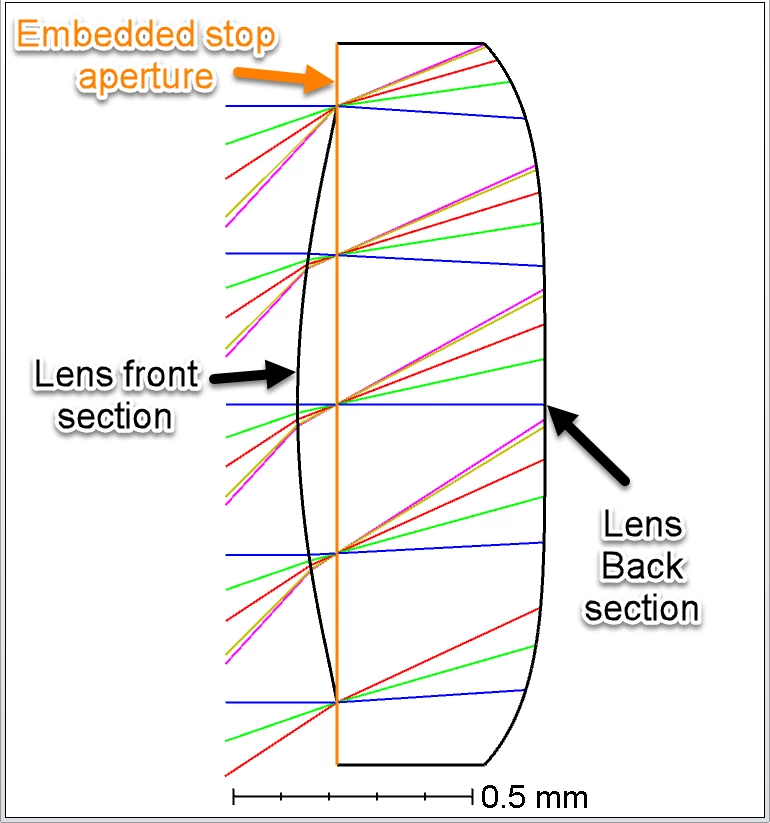
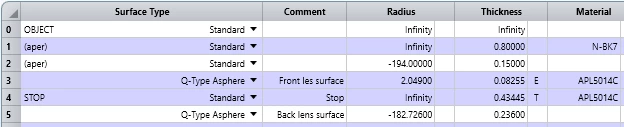
The main benefit of modeling the stop in such a way is that the rays do not experience negative propagation, and the stop becomes physical since the entrance pupil is now the correct image of the stop. Additional benefits are that OpticStudio will now be able to sample the pupil uniformly, avoid unnecessary vignetted rays, and make better use of our recently enhanced ray aiming capabilities.
Note that the first curved surface can also be used as the stop, but the Huygens-Fresnel principle indicates that this is not a physical solution either.
While embedding the stop is our recommendation, we want to hear from our users. What do you think? Are you choosing a physical stop?