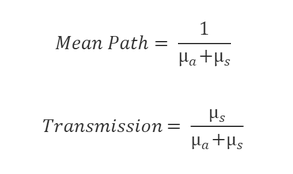Dear Sir/Madam,
I was trying to make a humen skin in zemax, I found a knowlendge base article on humen tissue/skin design: here is the link- https://support.zemax.com/hc/en-us/articles/1500005579202-How-to-model-the-human-skin-and-optical-heart-rate-sensors-in-OpticStudio
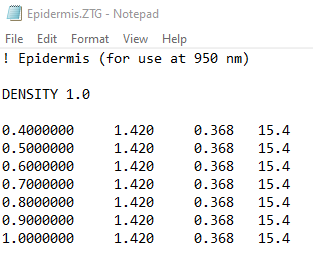
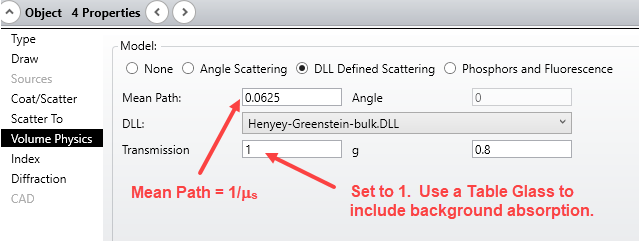
In this article all the related values for humen skin model is given, like refractive index, scattering anisotropy (g), u_a, u_b(please refer to the above link). From these given data I can calculate the “mean free path”, “transmittance” by the simple formula given there in article. I had manually calulated mean free path and transmittance based on the values and formula given there in above attached article. I had put all this claculated under “object properties” “Volume Physics” with “DLL defined scattering” to have scateering from different layers of tissue/ skin so far so good,
But, for verification of my design when I analyzed these values in the zemax file attached there in the above attached article, I saw that, there they are using some other value (values are not same that I have calculated using formula and values given there). So, I am wondering which one is correct? wheather the attached zemax file in that article, or the design that I made on my own with same approach with calculated values based on formulas and values?
I am attaching the value that I got based on calculation and that is given there in attached file in above article.

Regards,
Chandan Maurya