Hello,
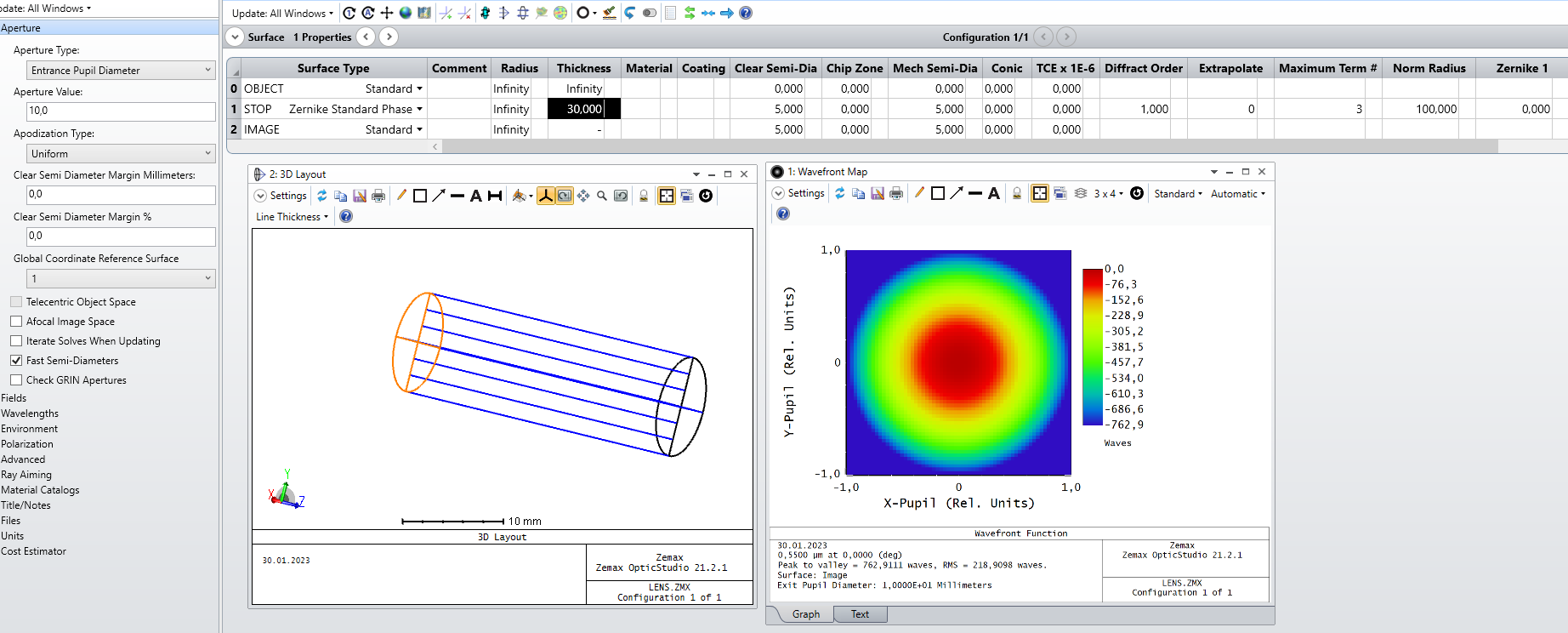
I would like to analyze the wavefront map for different zernike coeff. and I noticed that if I change the distance to the image plane (30 mm in this case for example in the figure), the whole wavefront changes accordingly and I don’t understand why.
if the source is coherant, the aberration in the wavefront should not change as it propagates. if not, then what is the relation? If this means that the surce is not coherant, then how can I make sure it it?
Thank you in advance.