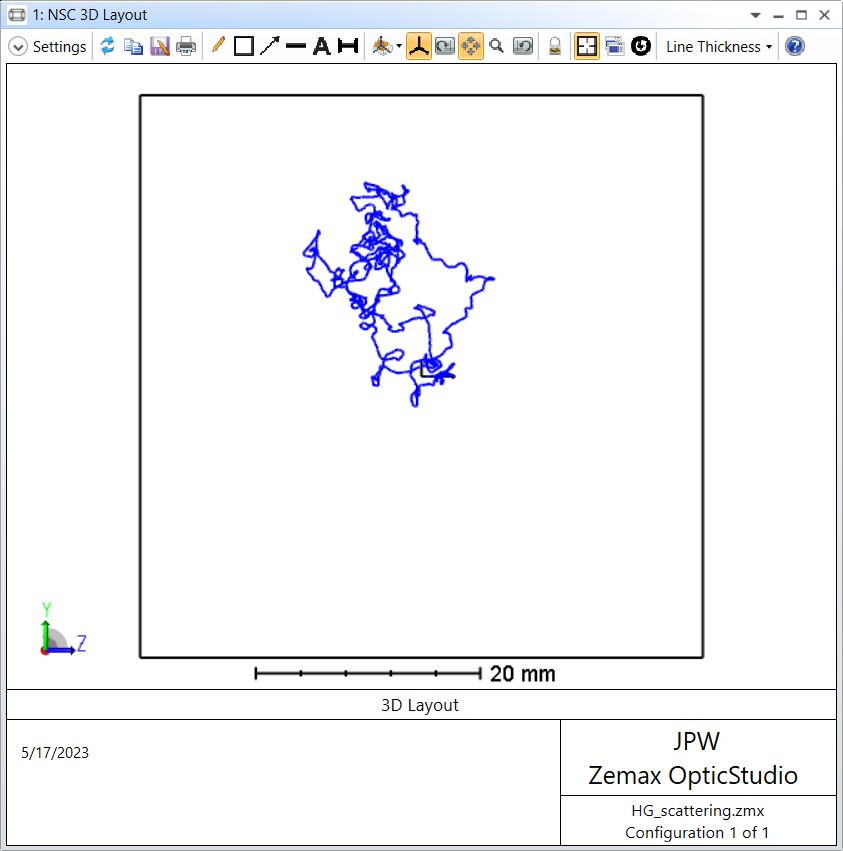
Hi, I want to measure the time of flight from rays scattered from thick diffusive media, e.g. a 5cm thick block of foam, resin, human tissue, e.g. 30-100 Transport Mean Free Paths, but I am finding hard limitations with the OS settings (see attached files).
As a general example, using the volume physics dialogue box, DLL defined H-G_bulk: using mu_s = 11.5 mm-1, mu_a = 0.0016 mm-1 and g=0.87, Mean Path=0.09 mm and T = 0.99.
Setting intersections to max: 4000, and segment number to 100k, with Min Rel Intensity (min) 1E-36 (to collect everything as rays can lose many orders of magnitude). This arrangement flags the “Error: Not Enough Intersections Allocated to Finish Ray Trace” for several cm of diffusive media, and indeed if I ignore this, a histogram of #segments shows it is clipped at 4000 (see ZMX and pngs attached). For context I measure the OPL of a ray by using the ray coordinates as vectors (* refractive index) per segment and summing. Splitting is turned OFF because the ZRD lists the splitting branches per ray together and this method would not work.
Questions:
- For my chosen H-G parameters, (Mean Path < 1, T-->1, g-->1), I know that the extreme scattering limits the number of rays I detect at the output of the scatterer. However, is my limiting factor really 4000 intersections/segments? And are these synonymous given my ZRD is only populated with #segments<4000 in the example shown? This would mean that Optic Studio can’t simulate turbid scattering through dense, thick materials like biological tissues, resin or foam, unless those materials were razor thin. I would ideally want to simulate scattering through 50+ transport mean free paths. It just appears that this 4000 value is an unfortunate ceiling to my simulation and where I need to take it.
- Are there any references behind the Henyey-Greenstein-bulk.DLL , e.g. where do the equations Mean Path = 1 / (mu_s + mu_a) and Transmission = mu_s / (mu_s + mu_a) come from? This is just to dispel any confusion in using the empirical coefficients in future simulations.
Thanks for your time,
Kevin