Hi there Zemax community,
In the past I have posted the following two questions related to what I want to do:
I am still trying to figure out how to properly import my rays into Zemax in the non-sequential mode.
What I ended up doing now, is that I sample N points from two separate uniform random distributions ( from 0 to 1) and then apply the following expressions:
phi = 2 * pi * u
theta = arccos(2v - 1)
with u and v being arrays of N random numbers from the uniform random distributions mentioned above.
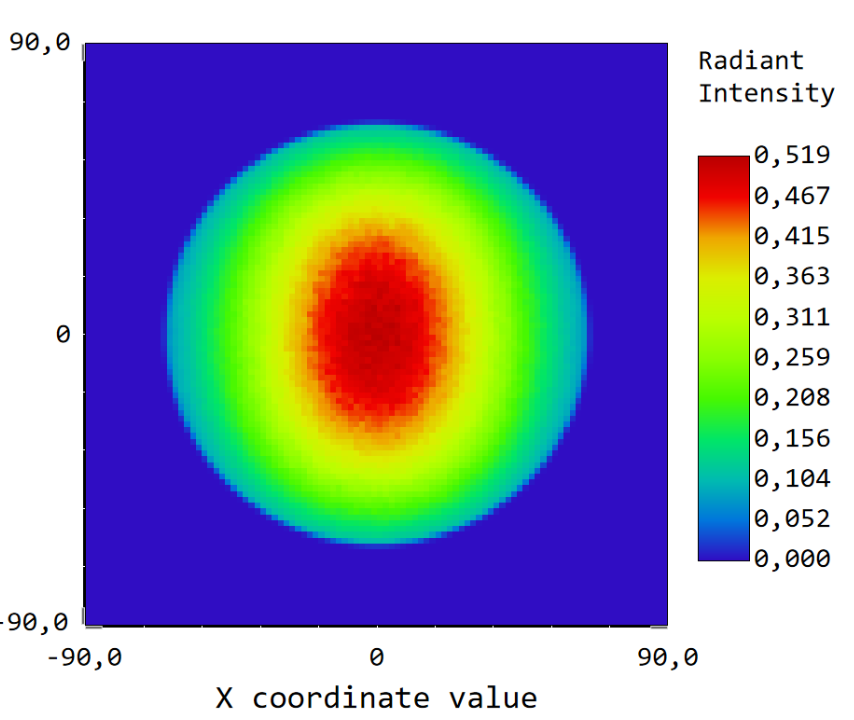
Then, using phi and theta, I sample my intensity function (which is expressed as a function of theta and phi) at the random coordinates phi and theta.
Finally, using phi and theta I assemble the direction cosine components and export the associated ray data file as a .DAT file following the documentation from Zemax’s help file.
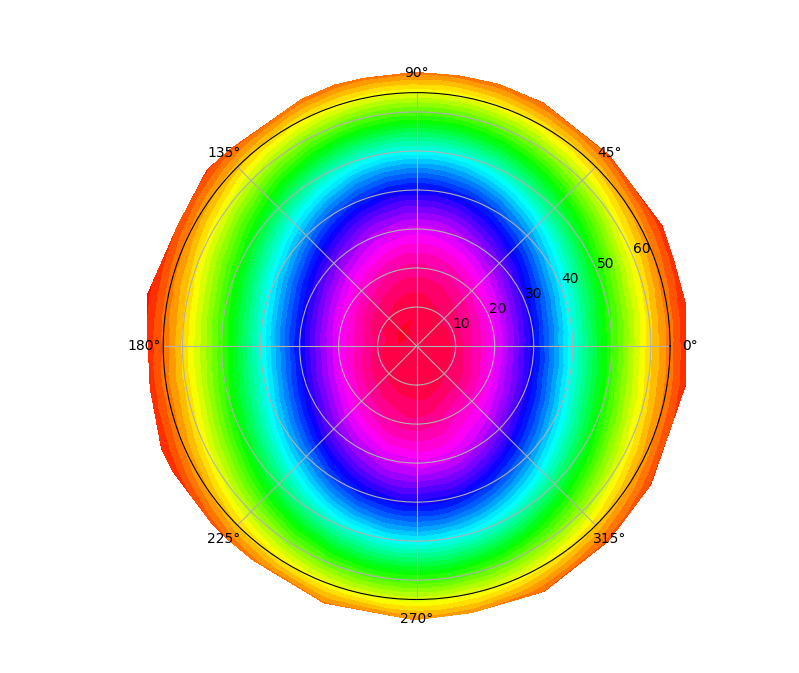
After importing the ray data set into Zemax, this is what I obtain:
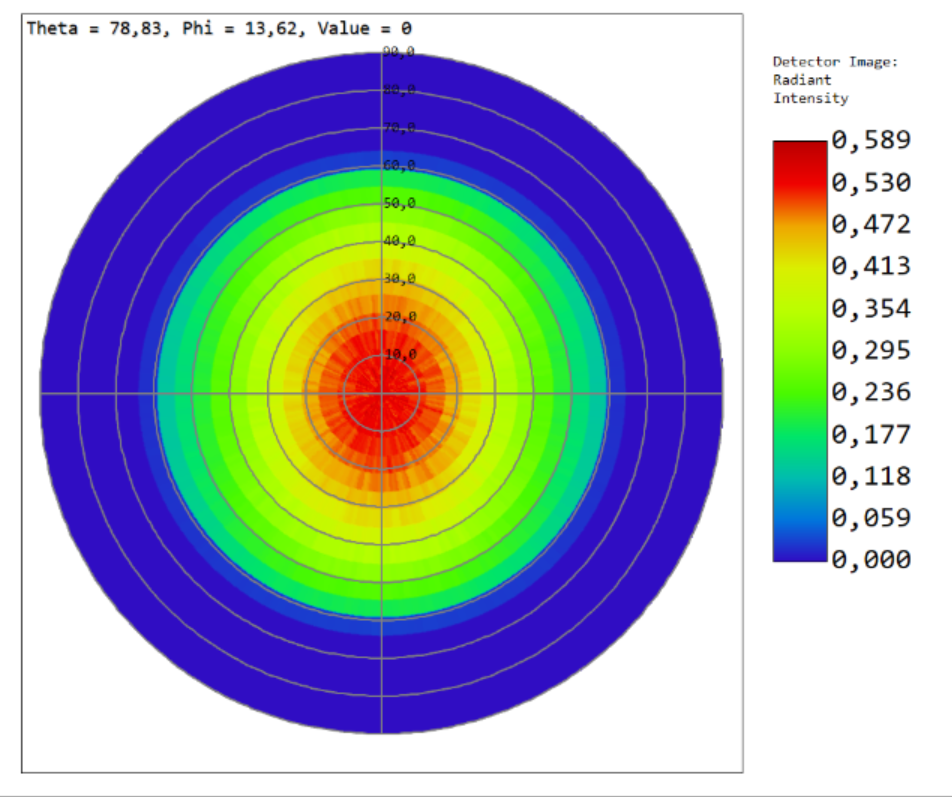
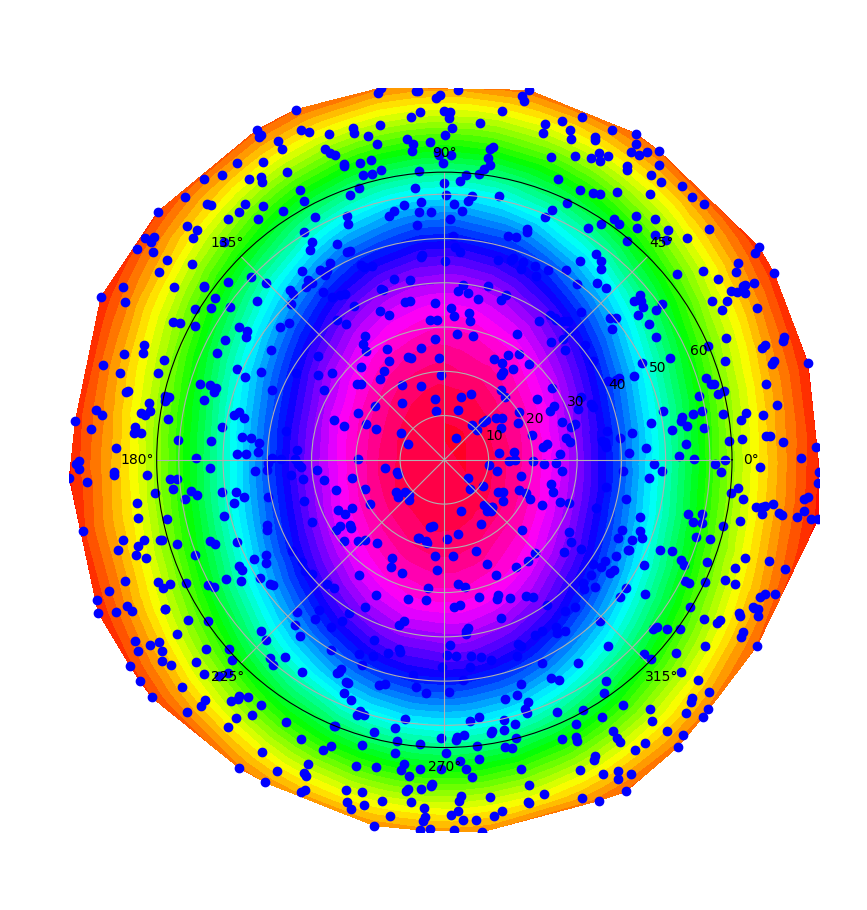
What I show above is the results from a polar detector. The pattern is somehow there but I can still see that the results are noisy and not smooth as I would expect from my original intensity profile:
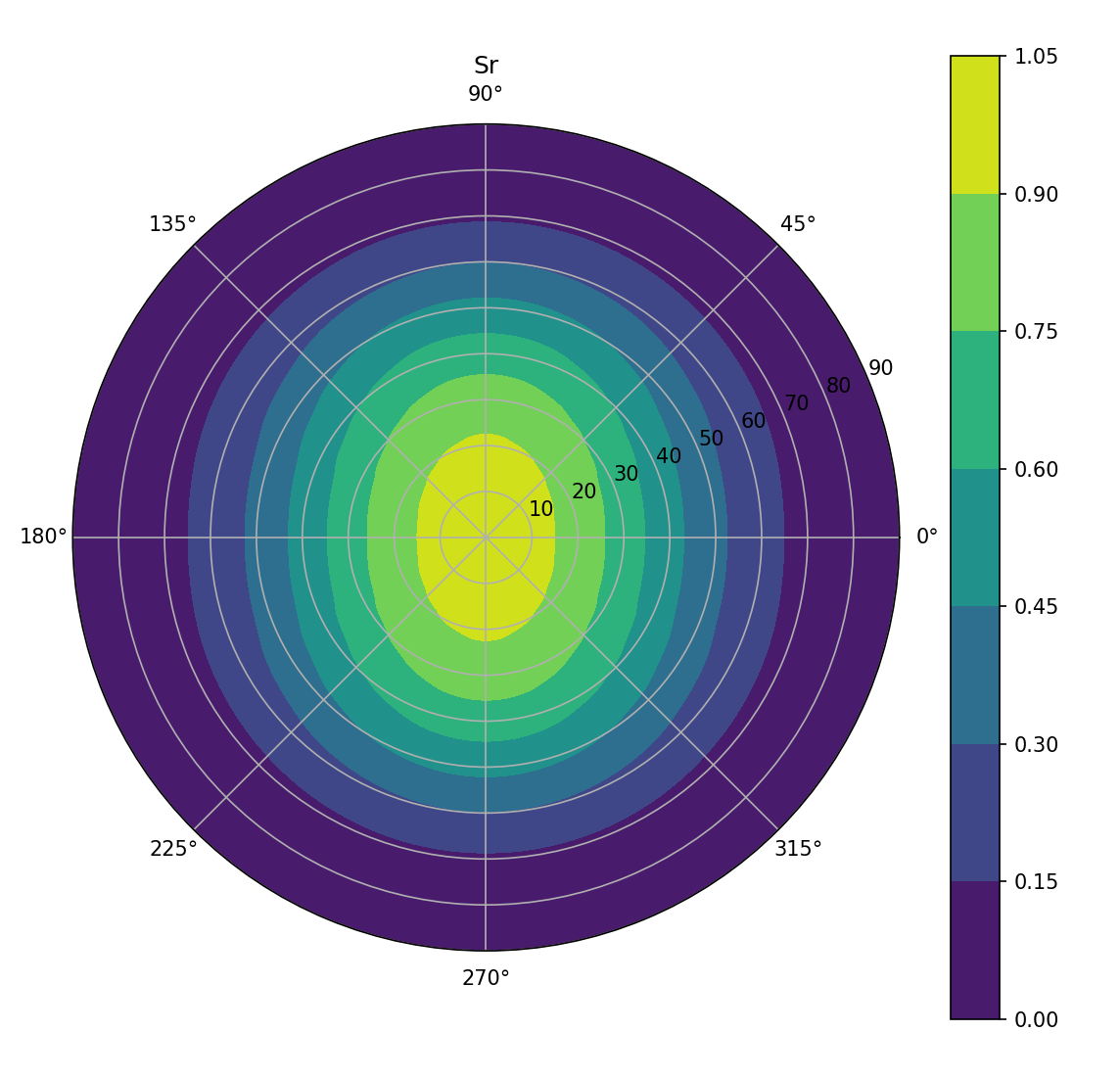
What could be happening here? What could I do in order to obtain a smoother output on my detector? (My ray data set contains 3E7 rays)
Thanks in advance