Skip to main content

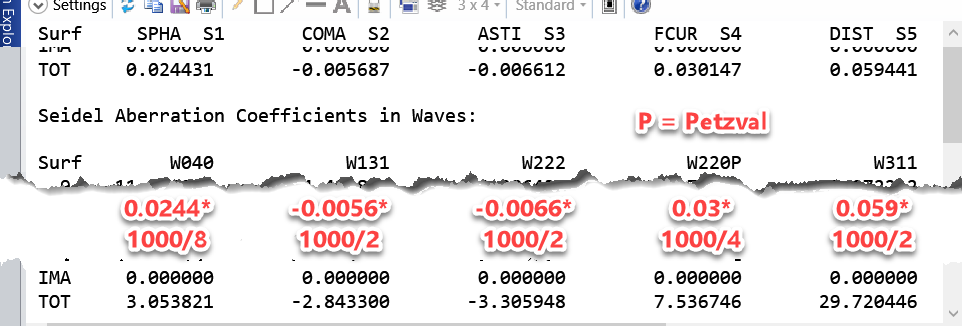
Quote from help file: The Analyze Tab (sequential ui mode) » Image Quality Group » Aberrations (Image Quality Group) » Seidel Coefficients

OpticStudio will compute the unconverted Seidel, transverse, longitudinal, and some wavefront coefficients. The Seidel coefficients are listed surface by surface, as well as a sum for the entire system. The coefficients listed are for spherical aberration (SPHA, S1), coma (COMA, S2), astigmatism (ASTI, S3), field curvature (FCUR, S4), distortion (DIST, S5), longitudinal color (CLA, CL), and transverse color (CTR, CT).

  1. The values displayed in the seidel diagram are the coefficients, and the values in merit function operands are in waves. Both values can be found in the seidel coefficients analysis feature.
  2. The units are always the same as the system lens units, except for the coefficients measured in waves.
  3. When converting the coefficients in lens unit to the wavefront aberrations in waves, we need to use the below conversion. (Note W220P is the Petzval curvature, it uses S4 = 4W220P)

 

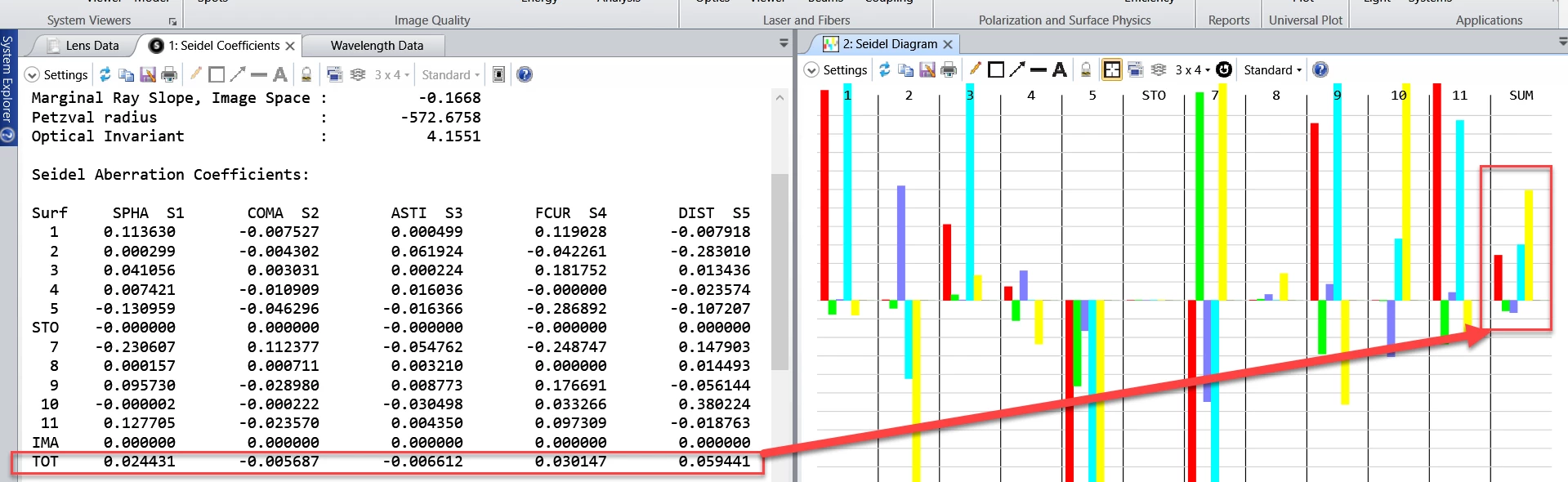
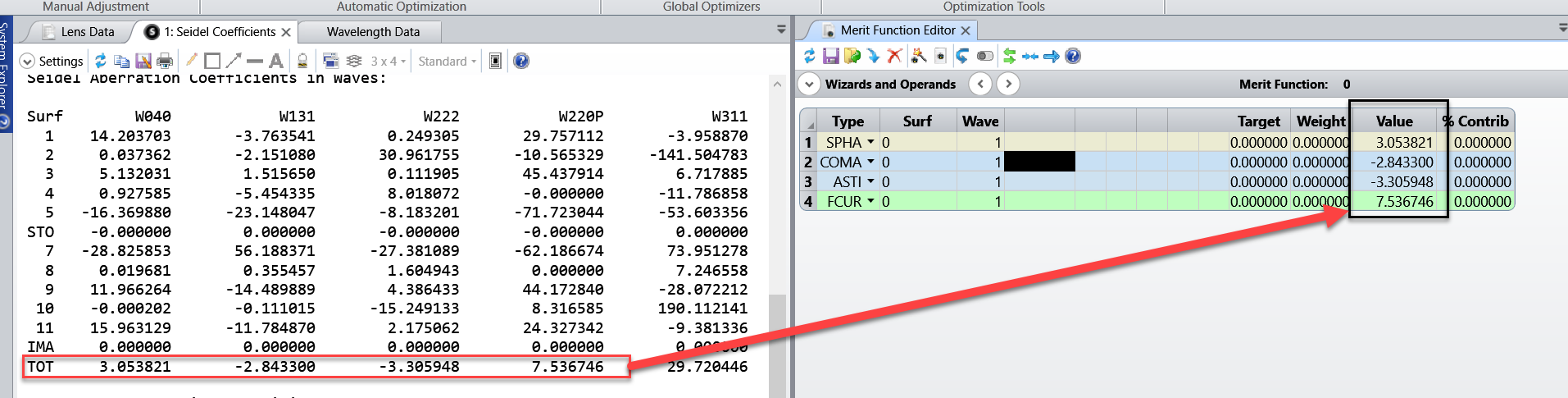
The sample file is attached for your reference. The wavelength is set to 1 um to simply the conversion between the lens unit and the aberration in waves. factor: 1mm/1um =1000

 

The sample file can’t be attached… I will try later..

 

Hi Yuan,

A couple of questions. 

  1. What is meant by “unconverted” Seidel coefficients?
  2. Wouldn’t it make sense to include an option to plot the coefficients in waves?  See this post:

Thx,
Jeff

Hi Yuan,

A couple of questions. 

  1. What is meant by “unconverted” Seidel coefficients?
  2. Wouldn’t it make sense to include an option to plot the coefficients in waves?  See this post:

Thx,
Jeff

Hi Jeff, 

Many thanks for your comments!

1, My understanding about “unconverted” is compared with the wavefront aberrations in waves.

2, Good point! I will submit a feature request. May I add your name in the list as well?

Hi Yuan,

Ok, thanks.  Yes, please submit a feature request and add my name.

With the current Seidel diagram, the user sees a comparison between the S coefficients, but as you show above, the S coefficients are related to their corresponding wavefront aberrations by various multiplicative factors (which, as far as I can tell, come from Seidel’s original work in ~1840) .  For example, S1 is eight times larger than W_040, while S2 is only two times larger than W_131.  These scale factors seem rather arbitrary.  So, it doesn’t really make a lot of sense to show S1 relative to S2 on a graph, when what is physically more meaningful is a direct comparison of W_040 (spherical in waves) to W_131 (coma in waves).

Regards,

Jeff

Hi Yuan,

Ok, thanks.  Yes, please submit a feature request and add my name.

With the current Seidel diagram, the user sees a comparison between the S coefficients, but as you show above, the S coefficients are related to their corresponding wavefront aberrations by various multiplicative factors (which, as far as I can tell, come from Seidel’s original work in ~1840) .  For example, S1 is eight times larger than W_040, while S2 is only two times larger than W_131.  These scale factors seem rather arbitrary.  So, it doesn’t really make a lot of sense to show S1 relative to S2 on a graph, when what is physically more meaningful is a direct comparison of W_040 (spherical in waves) to W_131 (coma in waves).

Regards,

Jeff

 

Many thanks for the description you offered Jeff! The feature request has been added and I am working on finding more votes to increase the possibility to get it implanted. 

Great, thanks! 

By the way, here is what Welford says about the Seidel sum values after he goes through their derivation:

 

So, the numerical factors relating the S & W terms are not arbitrary, as they follow from the derivations, but the “customary” convention to simply drop these scale factors from the Seidel sums makes the S values somewhat less meaningful compared to the corresponding W values.

Regards,

Jeff

Great, thanks! 

By the way, here is what Welford says about the Seidel sum values after he goes through their derivation:

 

So, the numerical factors relating the S & W terms are not arbitrary, as they follow from the derivations, but the “customary” convention to simply drop these scale factors from the Seidel sums makes the S values somewhat less meaningful compared to the corresponding W values.

Regards,

Jeff

Thank you Jeff for providing this piece of information. Yep, it’s more intuitive to show all W values in Seidel diagram~

Reply


Community Posting GuidelinesCookie settings


Zemax Community

Need more help?

To Chinese users:

Do not provide any information or data that is restricted by applicable law, including by the People’s Republic of China’s Cybersecurity and Data Security Laws ( e.g., Important Data, National Core Data, etc.).


不要提供任何受适用法律，包括中华人民共和国的网络安全和数据安全法限制的信息或数据（如重要数据、国家核心数据等）。



Privacy policy   License Agreements    Terms of use    Cookie Policy   Zemax Account Licensing Policies