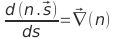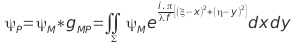Hello,
I am a new user of the OpticStudio software which arouses my curiosity!
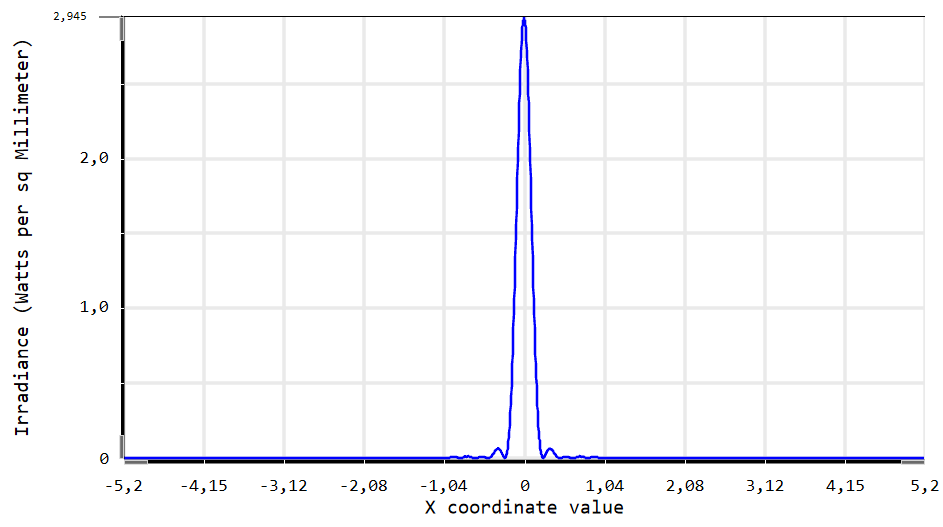
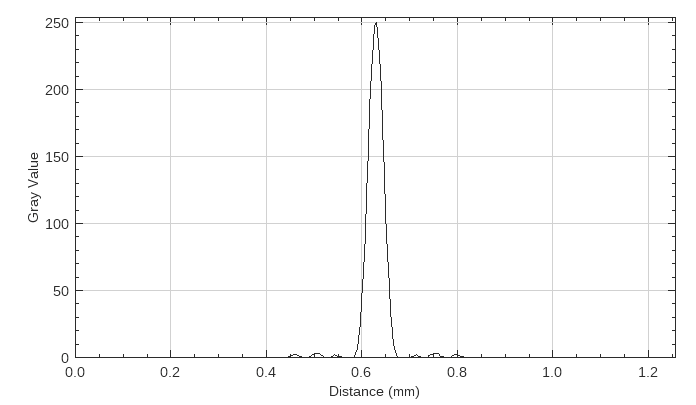
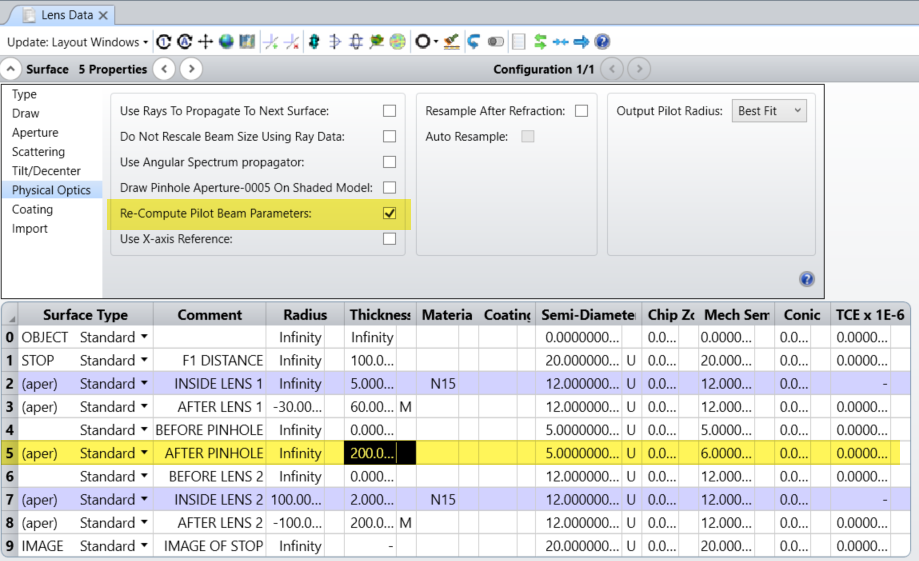
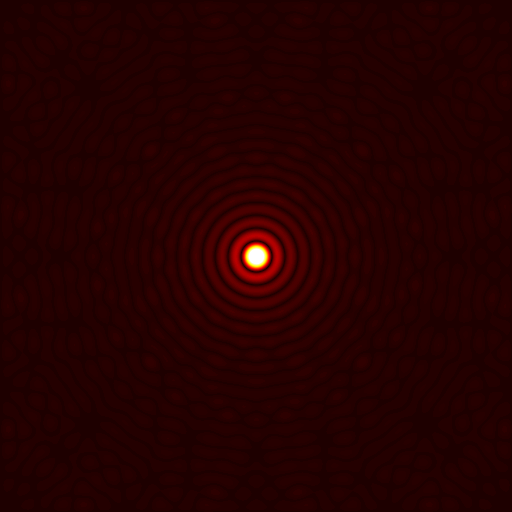
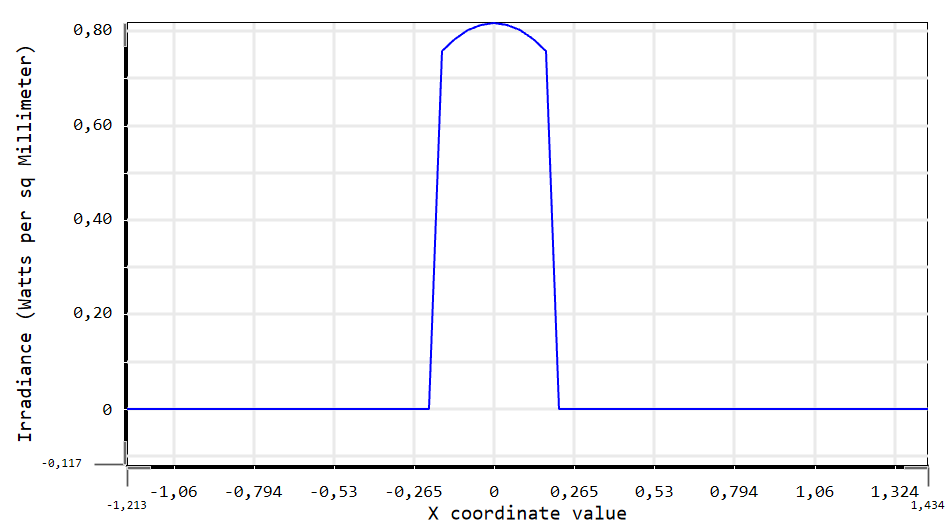
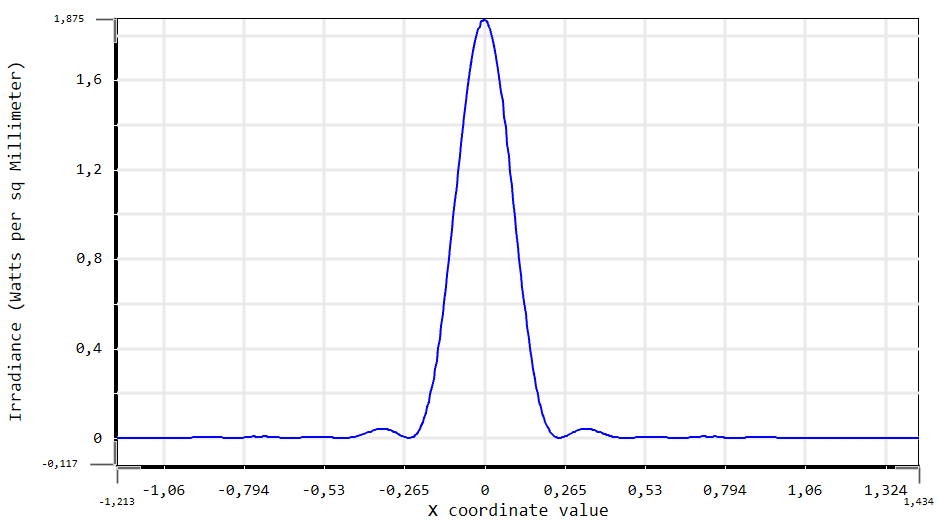
The wave propagation can be solved with several models and the software offers several possibilities. The model based on the astigmatic Gaussian beams (beamlets) is very well interesting.
But, I found few years ago the relevant paper:
Gosse L., James F., Convergence results for an inhomogeneous system arising in various high frequency approximations, Numer. Math. 90: 721–753 (2002).
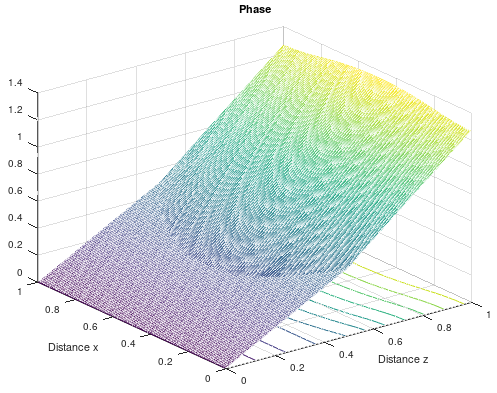
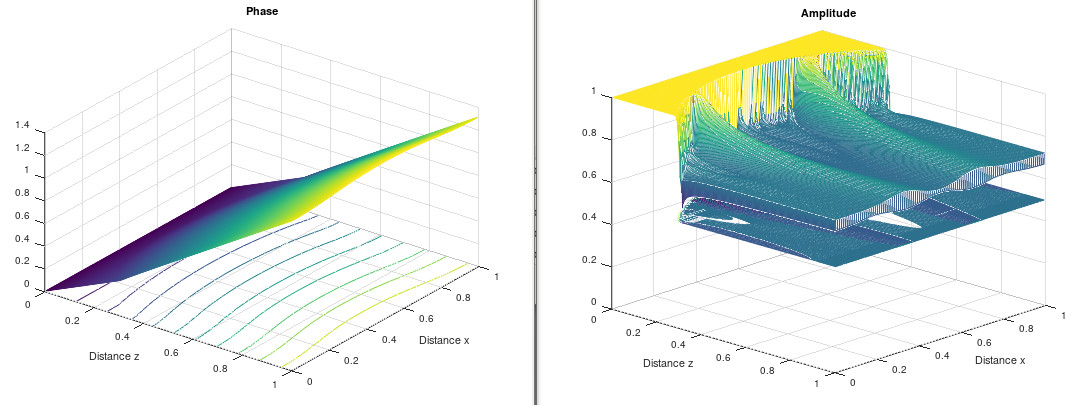
It is enough hard because the mathematics formulations are theoretic. However, the issue solving gives several possibilities to find the phase and the amplitude of the light wave together.
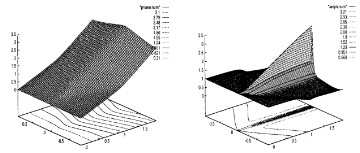
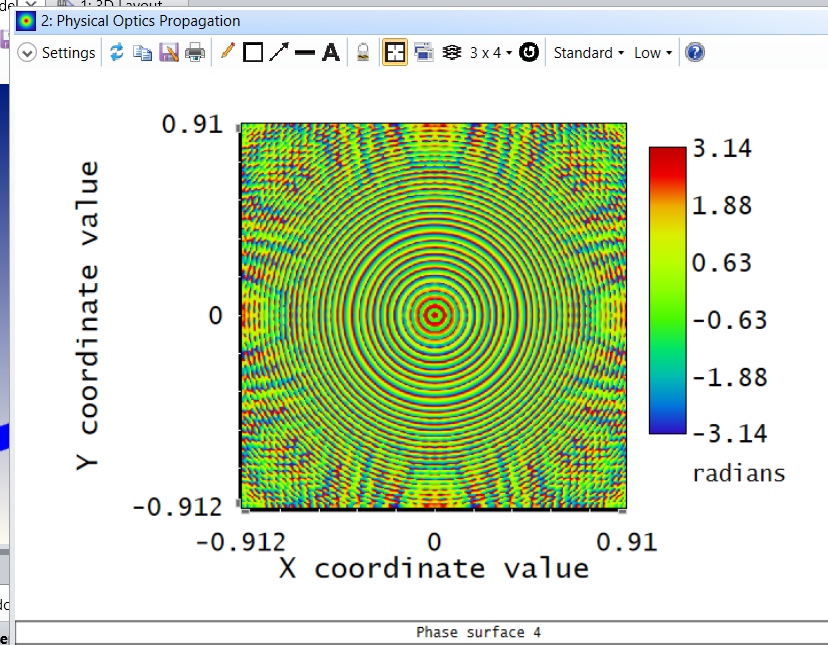
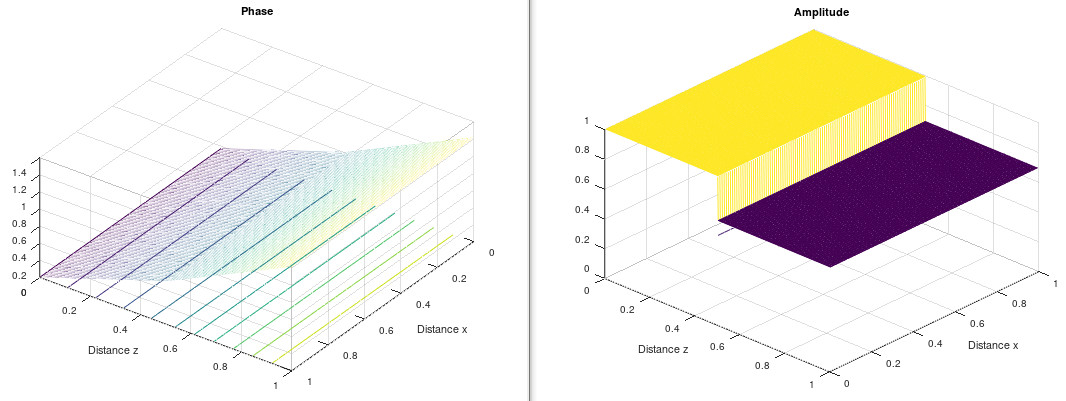
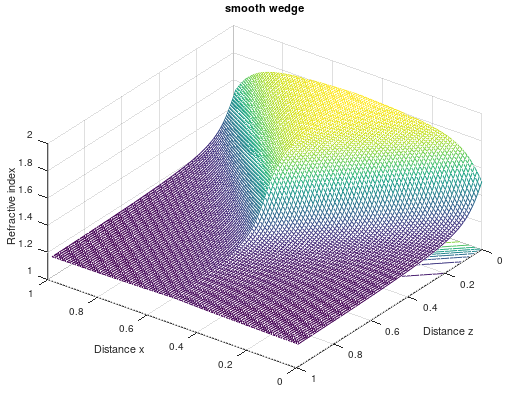
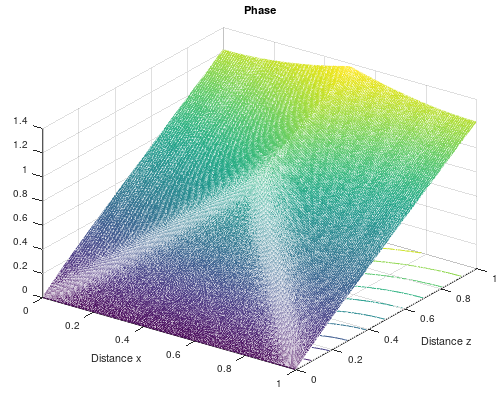
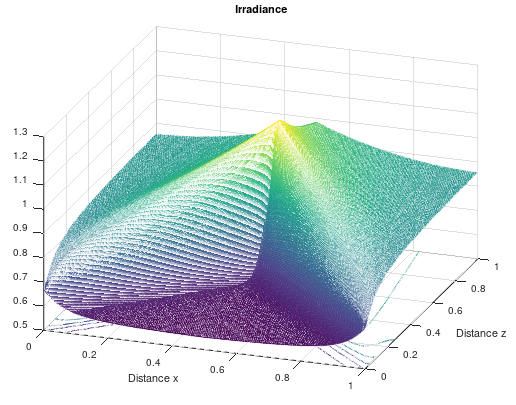
Numerical values for the phase and the amplitude of the smooth wedge.
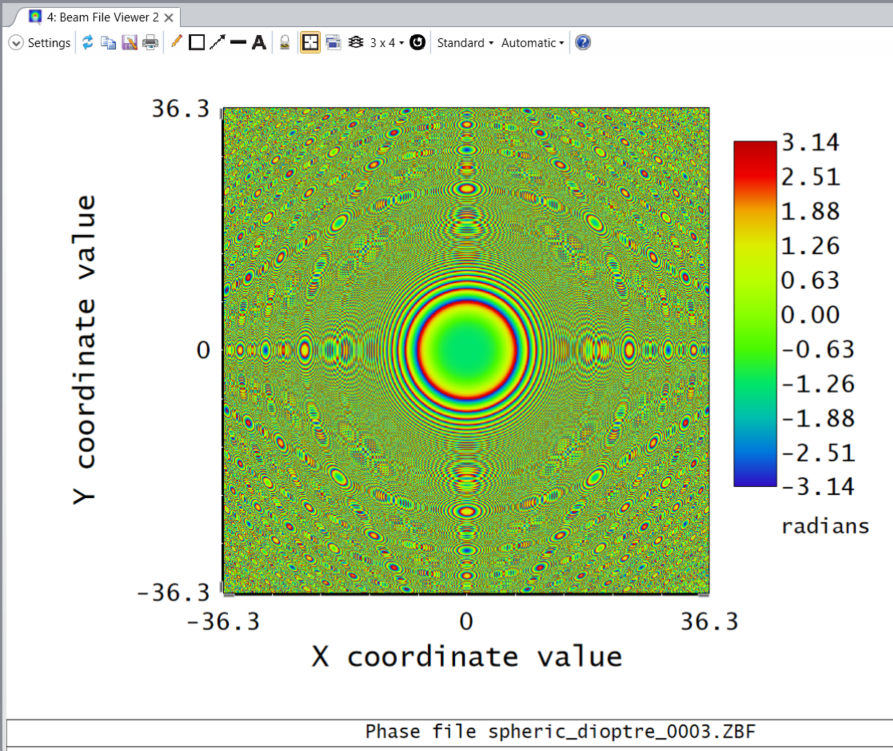
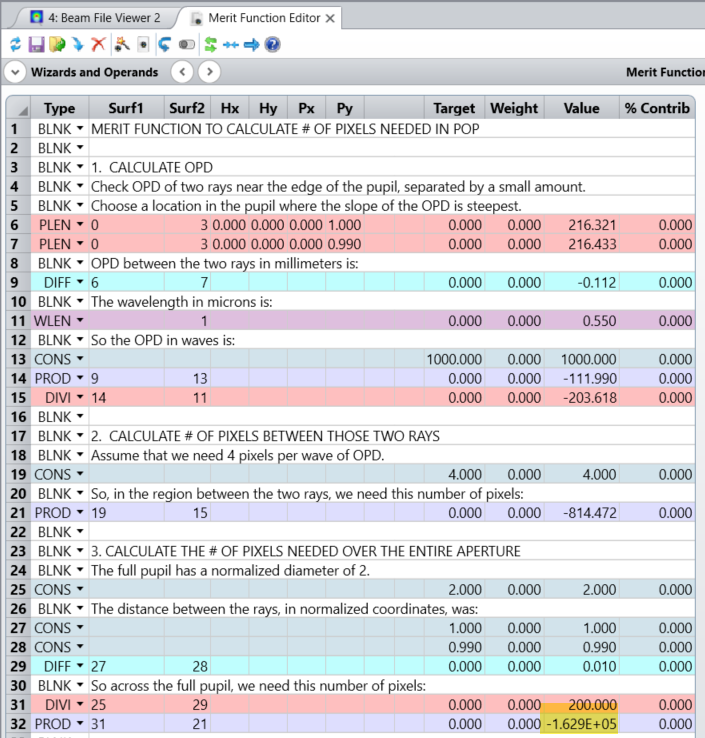
Therefore, do we have this possibility with the OpticStudio? Compute the phase in order to see transparency images for instance?
Thank you in advance for your answer.
Benoît.