Hi everyone,
I got the following, most simple setup consisting of only the gaussian beam source and a rectangular detector.
With a beam size of 0.15mm I expected to see the same as RMS Spot Radius on the detector viewer. But the detector displays RMS Spot Radius 0,10606mm which is 1/sqrt(2) of the given beam size.
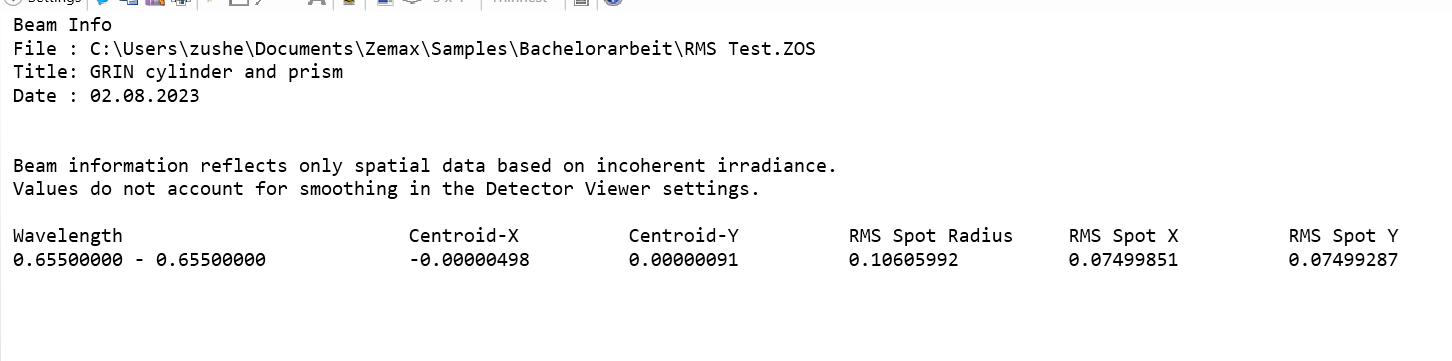
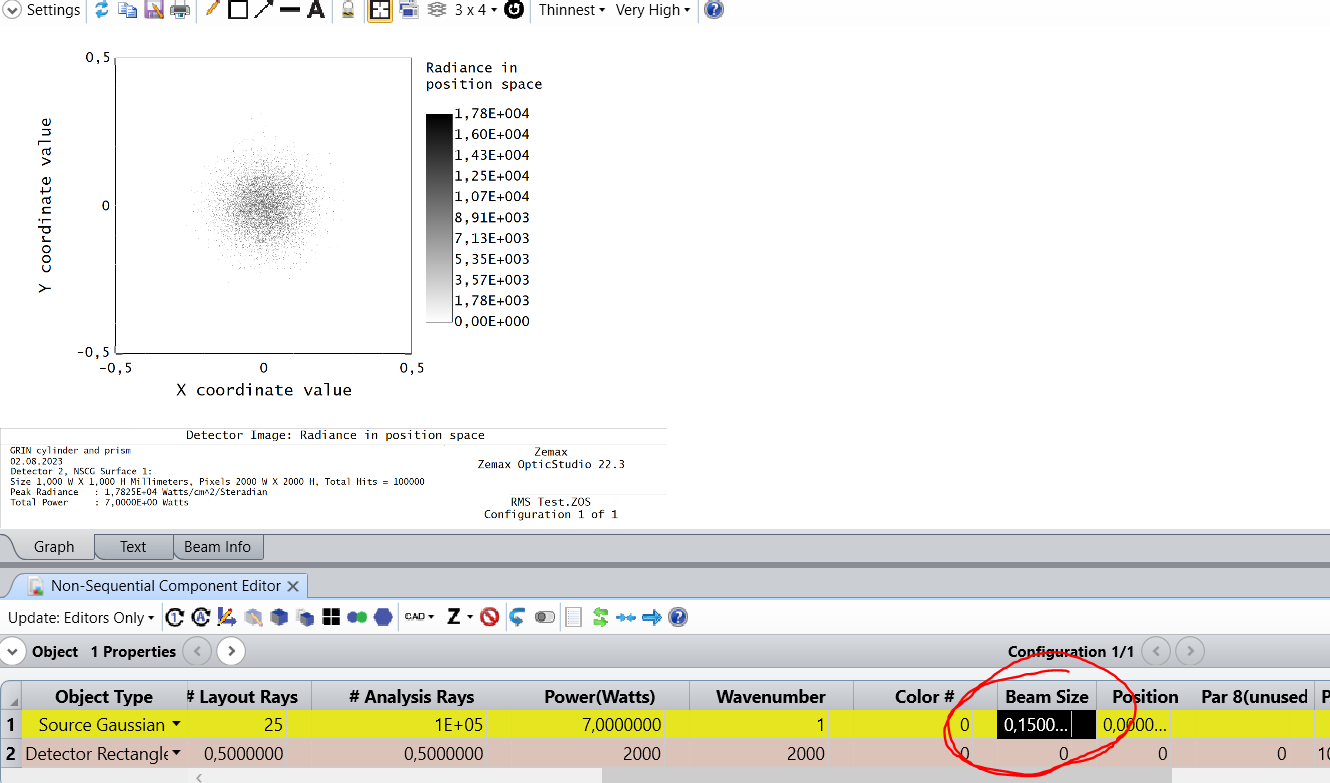
The beam size radius is where the residual intensity account for 13.5% of the peak intensity. It should therefore be identical to the RMS Spot Radius.
I just can’t wrap my head around as why the RMS Spot Radius is 1/sqrt(2) of the beam size, can anyone explain?
Is there a relation between RMS Spot Radius and Gaussian beam size that I am missing?
Sincerely,
Zu







