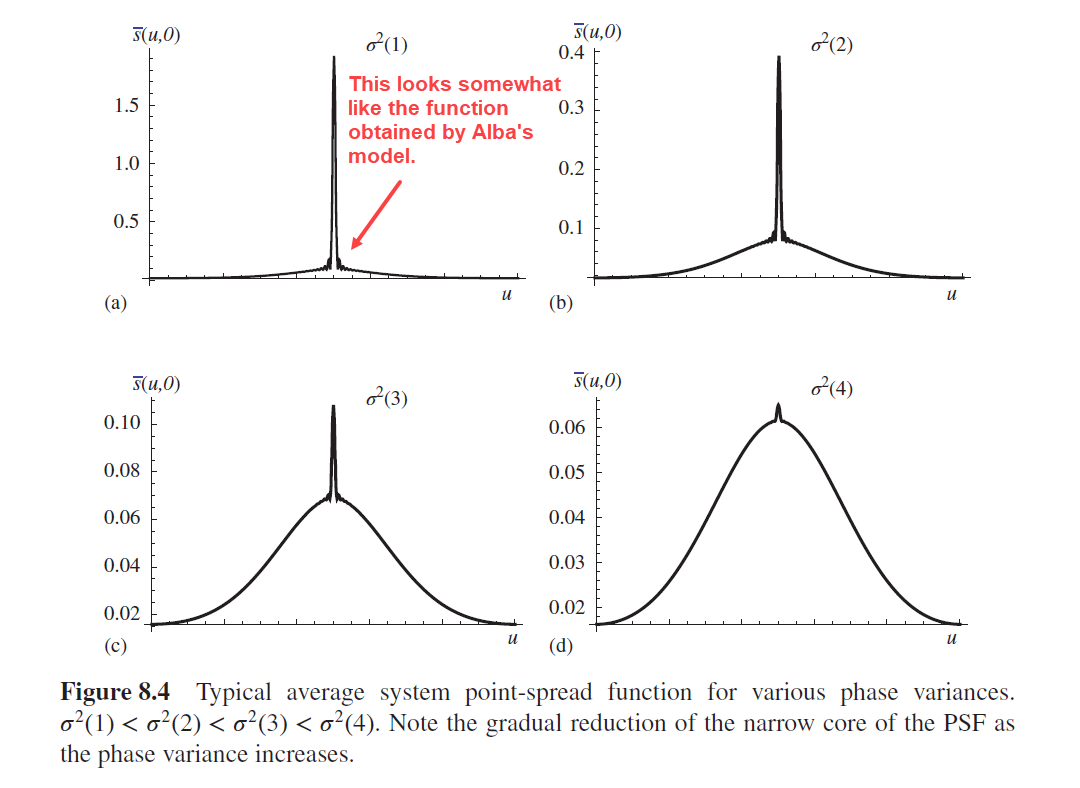
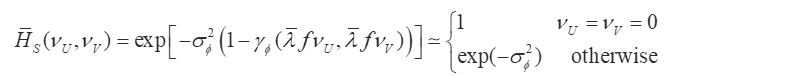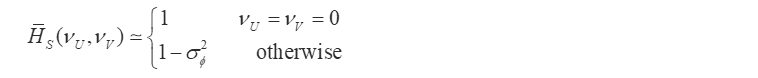Hi,
we are doing non-sequential simulations of surface roughness scatter, and would like to find a way to translate those into loss of contrast.
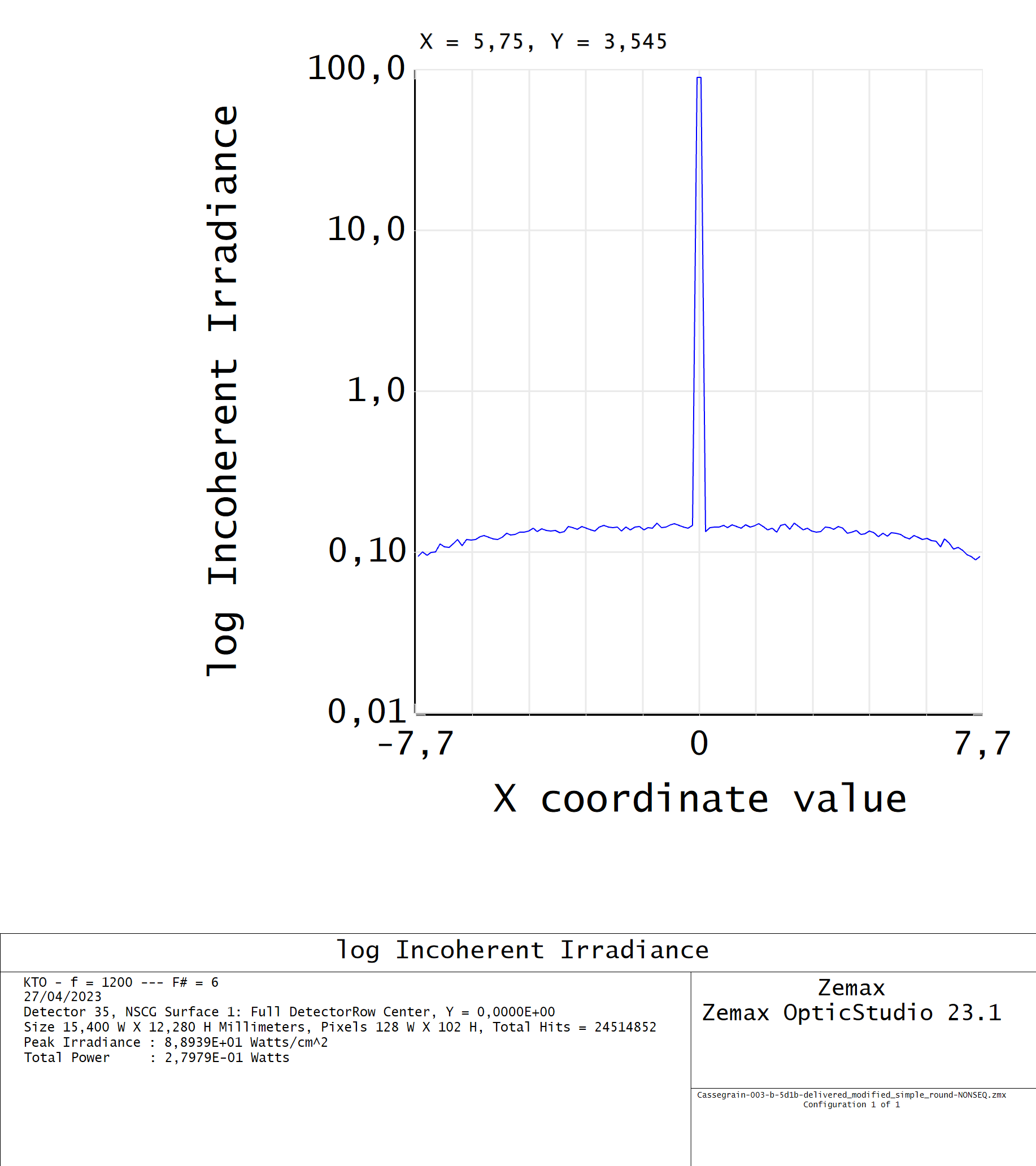
As an example, this is the type of irradiance profile we would get:
If you change the detector viewer to “Geometric MTF” you get this:
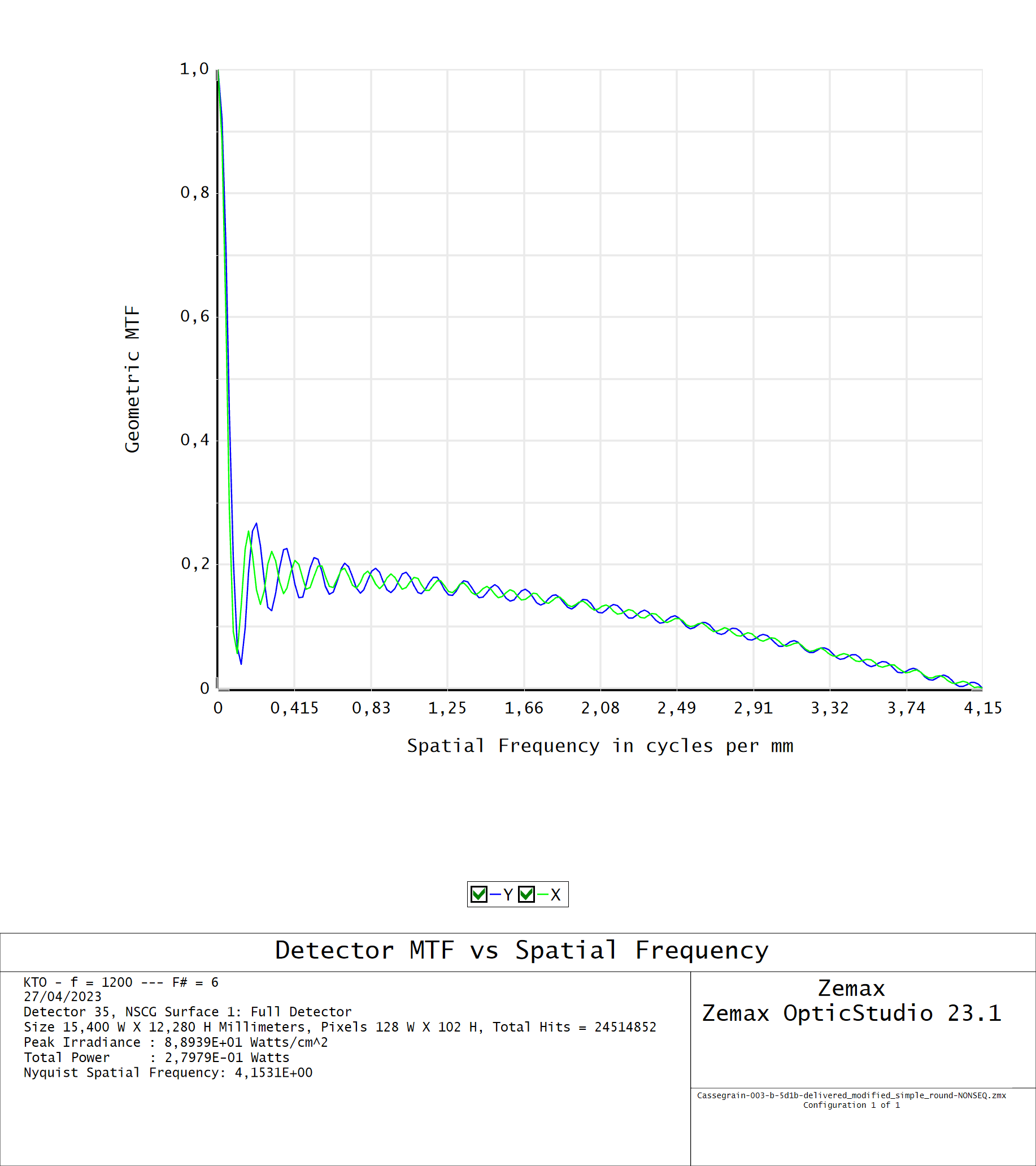
Which if I understand properly would be the Fourier transform of the “irradiance PSF”. The fact that the graph ends at 4.15 cyc/mm is because we are using pixels 10 times larger than the real detector to get enough SNR, so it’s a ten times smaller Nyquist frequency. But I don’t really know how to get any useful information on the loss of contrast from veiling glare in the image from this figure, if that is even possible.
Thanks in advance,
Alba