Someone recently asked how “easy” it would be to recreate a PSF from a given setup of MTF measurements. My first answer was “don’t do that” but I’m trying to quantify all the issues that are present with trying to recreate the PSF. Below are the major hurdles I see but I would love to get other people’s feedback into the feasibility/pitfalls that need to be considered:
A single scan MTF is essentially a FFT of a 1D cross-section of the PSF. If there is no rotation in the system, then the MTF is the FFT of the Y axis (tangential) and X axis (sagittal); there is no information about any data points that lay off the x/y local axis. To fully recreate the PSF, you would need to have multiple MTF scans at different angles.
The MTF is actually the absolute value of the OTF, so the MTF only has real values in it. The FFT/IFFT for any real-valued signal is always symmetric, so an asymmetric PSF cross-section can not be reproduced from the IFFT of the MTF, at least not without (a lot) of pre-processing. Q: is there a way to recover the OTF (imaginary part) from the MTF?
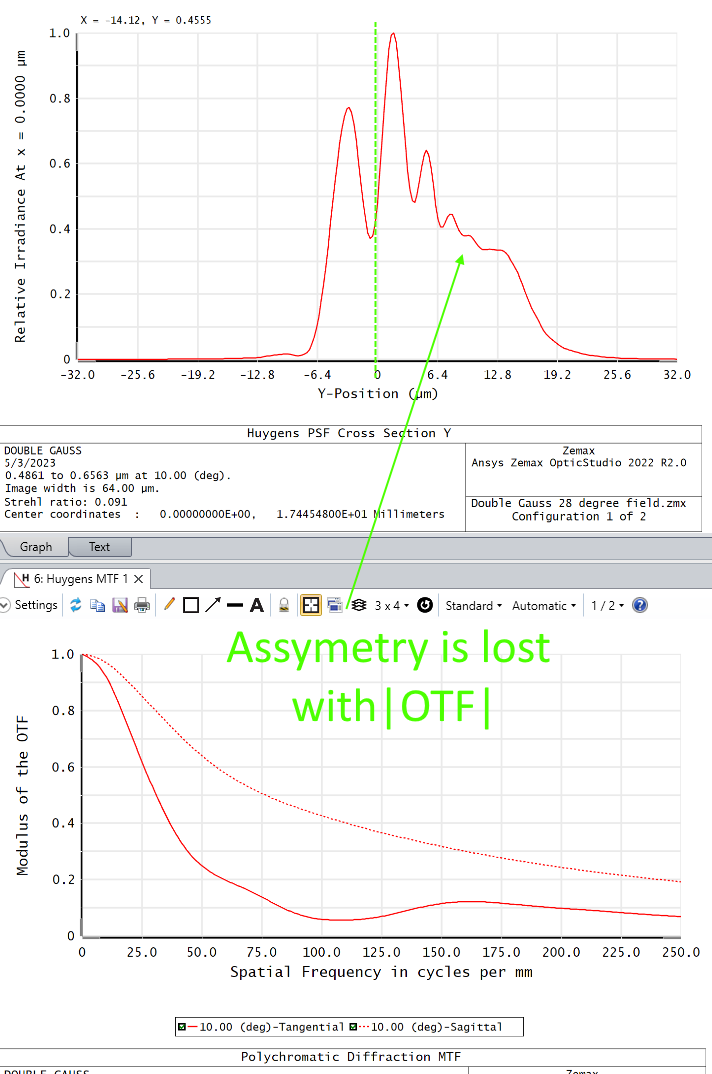
The MTF is always normalized to a value of 1.0, so there is no information about the Strehl Ratio/PSF peak. So even if the shape of the PSF can be recovered, if there are MTF scans for different field angles, you would not be able to scale the PSFs to the correct intensities.
Are there other pitfalls/limitations when trying to go from MTF to PSF? Are there any good papers that go into depth about this?
Page 1 / 1
Well, I’ll defer to whatever @Jeff.Wilde says but I think you’re correct that there’s no complete way to go from the real-only data of the MTF to the complex data of the OTF. Your initial ‘don’t do that’ reaction is probably correct
You could train a neural network with a series of MTF/PSF pairs, and then give it your measured MTF and get it to suggest matching PSFs. I suspect without proof that there will not be a single answer to the question, and there is likely to be a family of PSFs that can generate the required MTF. Good luck! And let us know how you get on.
Mark
Hi Michael,
Although I have never tried this myself, I think it may be possible to use a phase-retrieval technique to reconstruct the OTF from the MTF, and hence find the corresponding PSF. Because the intensity PSF is real-valued, it’s Fourier transform, the OTF, is Hermitian. However, there is no requirement that the PSF be symmetric. If the correct OTF can be recovered, then it would seem that the corresponding PSF should yield the proper peak value (Strehl ratio).
Again, I don’t have personal experience using phase retrieval, but it seems like there exists a large body of work in the area. For example, the interesting field of Fourier Ptychographic Imaging makes use of phase retrieval for high-resolution computational imaging (when illuminating with an array of LEDs).
Regards,
Jeff
Hey Mark & Jeff,
Thanks for the feedback & suggestions.
Jeff, from an initial look at the Fienup technique, it seems like it’s you are basically doing the following:
Create a “first guess” PSF
FFT the PSF to get the OTF (and keep this forward phase information)
Convert the OTF to MTF & compare the computed MTF to the measured MTF
Modify the “first guess" PSF based on the difference between the computed MTF and the measured MTF
Repeat steps 2-4 until the difference is below a threshold value
At this point, you would already have the PSF from Step 4. So, this essentially comes down to an iterative forward global optimization (at least if my understanding is correct). My description above is the technique I've been thinking about for going from PSF to Wavefront, which is essentially the same problem, just one step higher in the WFM->PSF->MTF calculation (I believe you can recover the actual phase of the WFM if you have multiple through focus PSF scans, but you would have to do an optimization if you only have a single PSF image). Using a Zernike Phase Surface with a Paraxial Lens to simulate the original f/#, you could optimize your Zernike terms until your simulated PSF matches your measured PSF. This would be going from a 2D WFM grid to a 2D PSF grid, so a single PSF measurement is okay. Since the MTF is the FFT of a 1D PSF cross-section, multiple MTF scans would still be required to remove ambiguity.
One issue, as with any global optimization, is determining if you’re at a local minima (wrong PSF which still produces an MTF within the threshold of the measured MTF) or you’re at the global minima (the actual PSF which produced the measured MTF).
If you have knowledge of the initial category of lens design which produced the measured MTF (infinite/finte conjugate, monochromatic, f/#, telecentric, wide FOV, etc), then another technique I was thinking of is building a Machine Learning model. You can take a handful of initial designs, perturb these lens with +10k Monte Carlo runs, and then feed in +1M PSF<->MTF datasets to train the ML algorithm. From a manufacturing/yield analysis then, if the ML algorithm gives multiple PSFs as possible candidates, then select the worst PSF candidate to incorporate into something like an Image Simulation (granted, I don’t know anything about ML and this is probably an incredibly difficult task).
Either way, it seems like there is no closed-form way of going from MTF to PSF but there are a lot of possible techniques for estimating a possible PSF candidate that could produce a specific MTF. Also, if you can play around with the initial data capture (through focus, DMD tilted images, etc), you have a lot more flexibility in the speed/accuracy of PSF reconstruction.
Thanks for the ideas/suggestions/confirmations.
Yes, various iterative algorithms exist, perhaps the best-known being the Gerchberg-Saxton version:
I’ve tinkered a little bit with the GS algorithm, but that was quite a while ago. So I can’t intelligently comment on convergence or solution-uniqueness issues. Machine learning certainly opens up another interesting possible avenue.
I too am working this problem.
I have opted for G-S and Monte Carlo to address the relationship.
MTF is a 2-D scalar field - just like WFE. With only (x2) cross-sections through the MTF, the problem is ill posed and not invertible. Therefore, Jeff’s approach of G-S is one method of attempting to propose a model that explains the observation. However, I suspect the solution is not unique (there is more than one WFE / PSF that will create the observed 2-D MTF cross section).
As a consequence, I’m tackling this problem by:
Assuming the WFE can be represented by a few Zernike coefficients (pick x9, … x36)
Selecting a random set of coefficients and then using a forward model to predict the MTF
Use multivariable optimization techniques to assess the most likely possible WFEs and hence PSFs
Contact me to discuss. This is a very active area for me and I would appreciate an offline discussion.
