Hi
I have done a microscope optical design on Zemax NSQ and want o check the PSF but don’t see it on my Analyze tab. Below are my options:

Can you please help me find out if I am missing something?
Best,
Hasti
Hi
I have done a microscope optical design on Zemax NSQ and want o check the PSF but don’t see it on my Analyze tab. Below are my options:

Can you please help me find out if I am missing something?
Best,
Hasti
Best answer by Jeff.Wilde
Actually, it is possible to calculate the PSF in non-sequential mode using the Detector Rectangle.
Details from the help documentation:
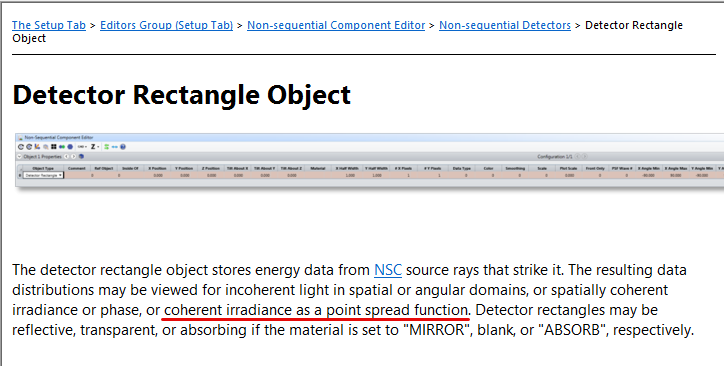

Here’s an example:
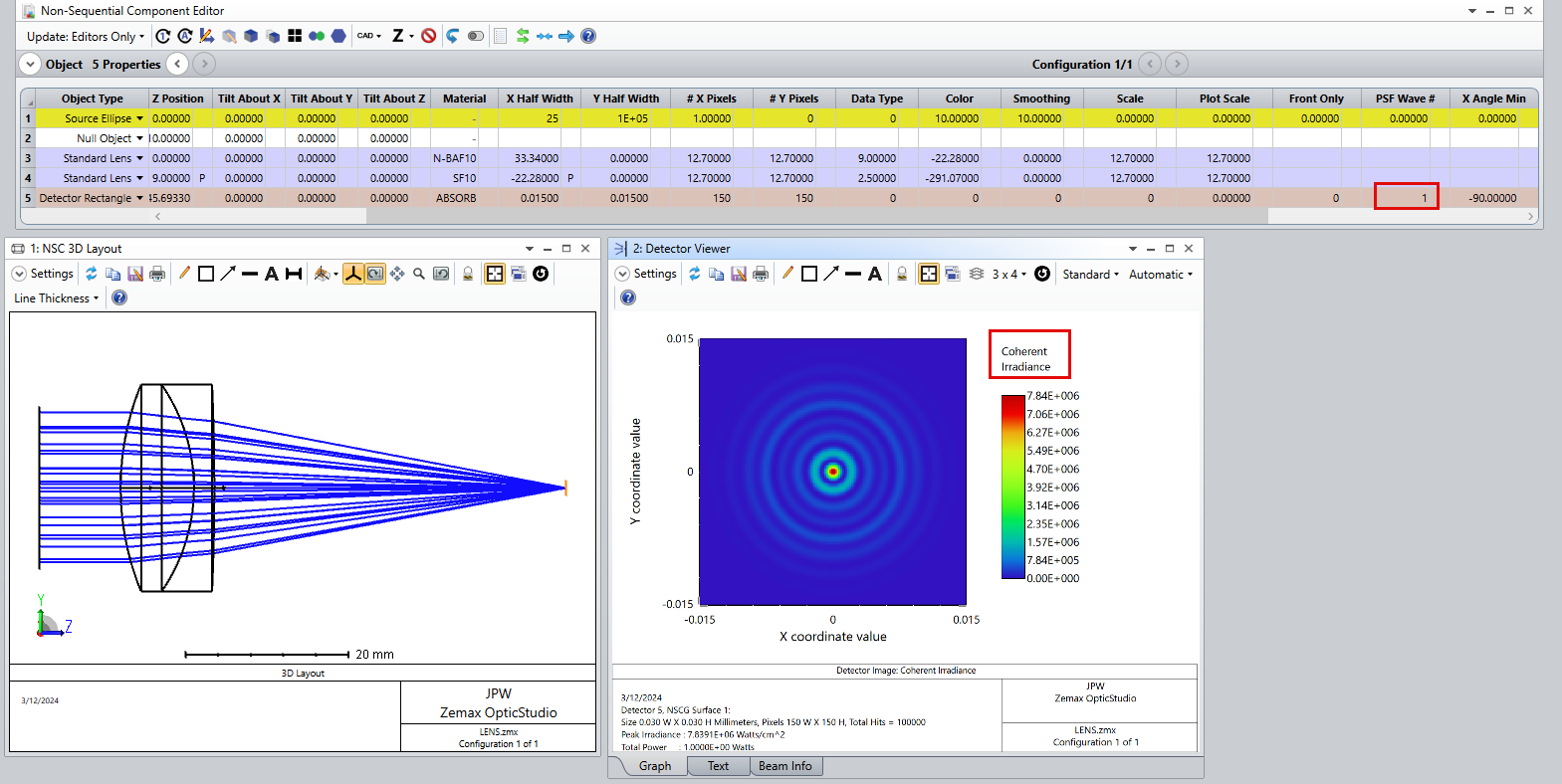
Of course the key assumption here is that the source beam has the desired size (e.g., it effectively fills the stop). That being said, I do agree with
Regards,
Jeff
Enter your E-mail address. We'll send you an e-mail with instructions to reset your password.