Hi everyone,
I got a problem in understanding the optimization in Zemax OpticStudio…
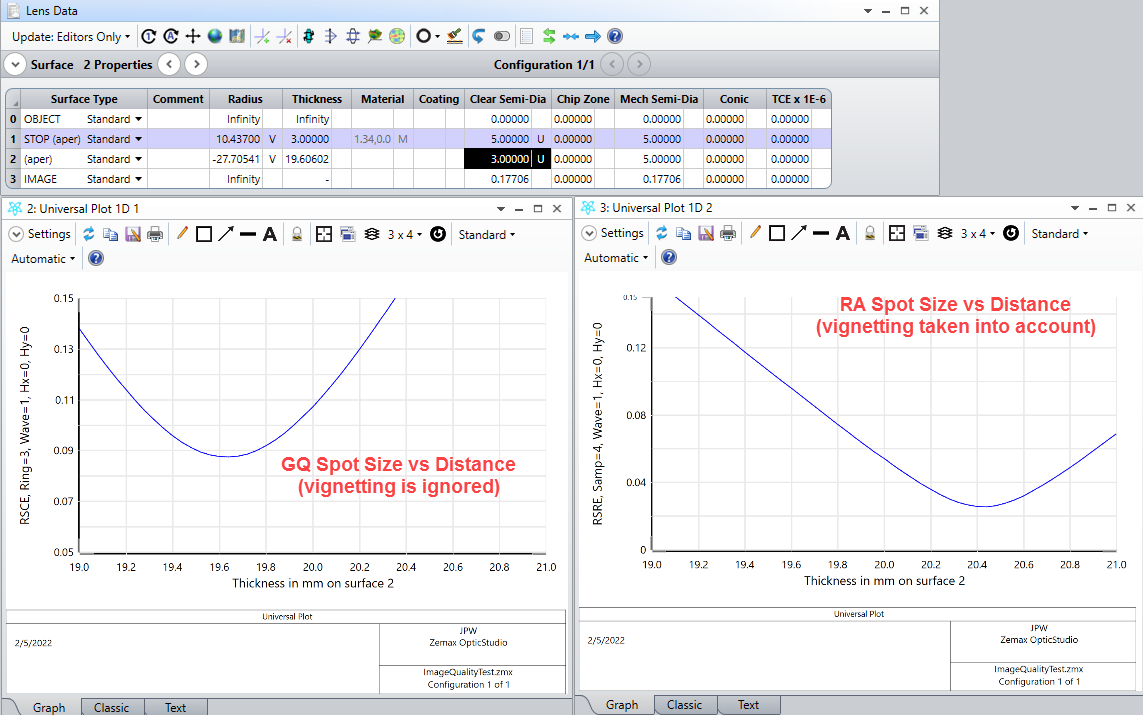
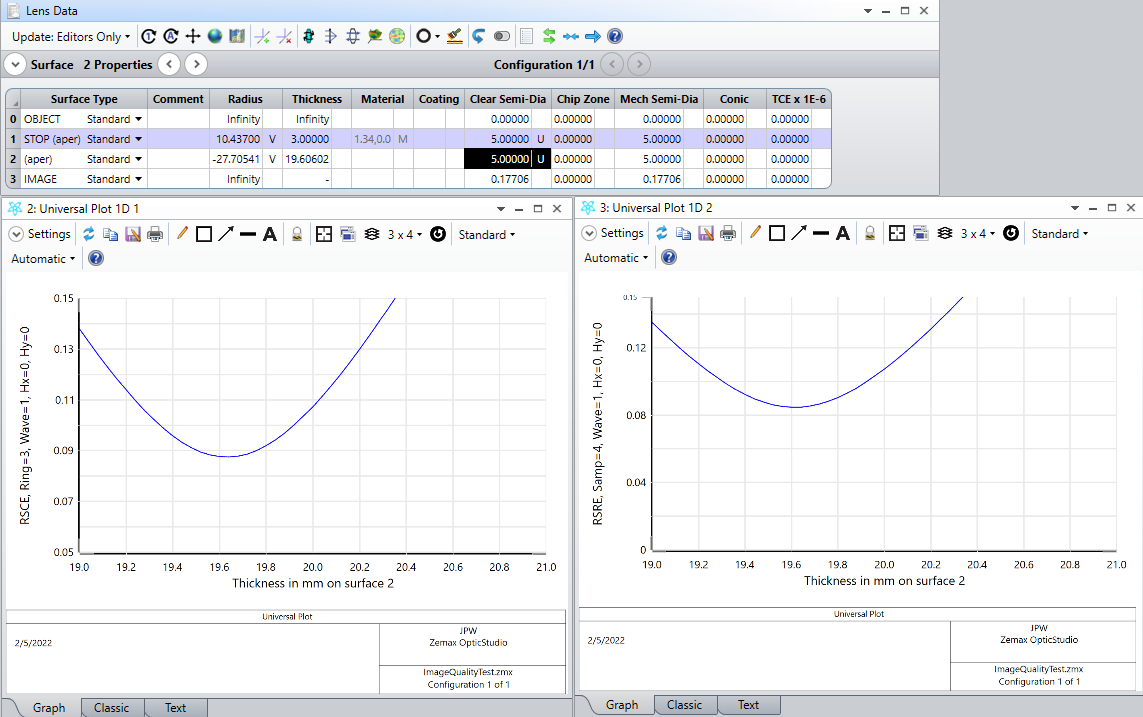
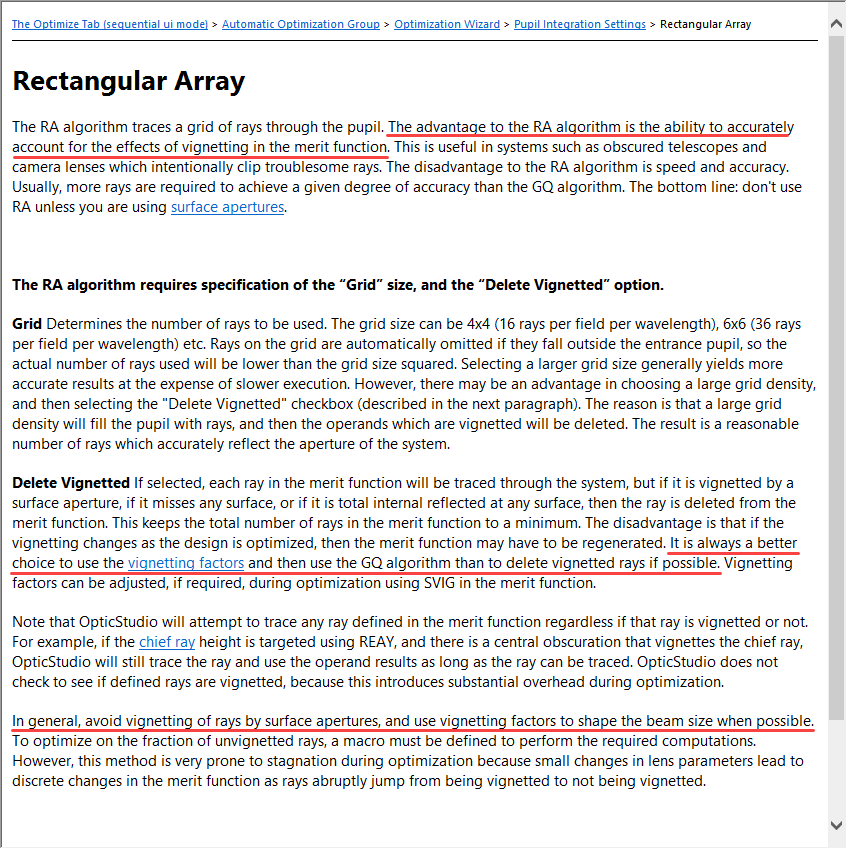
By doing a simple lens (with thickness T and radius of R1 and R2) and trying to optimize it on the spot image quality setting I don’t get the smallest RMS on the image plane. The optimal image distance of the smallest RMS after the optimization is always 1-2 millimetres after the image plane. Could someone help me to understand this? Why is it there and not at the image plane?
By testing I saw that changing the image quality option to contrast works way better to focus on the image plane…
I’ve added a simple model to show my problem…
Thank you in advice!