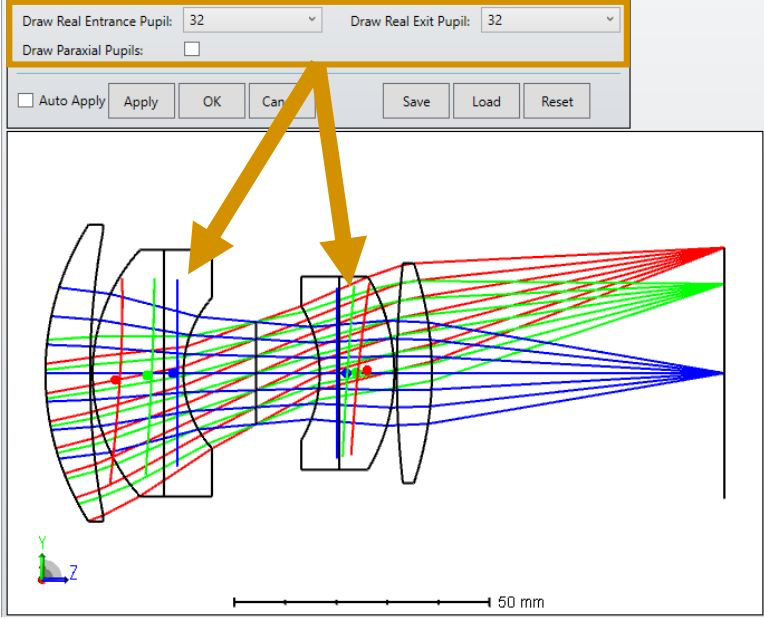
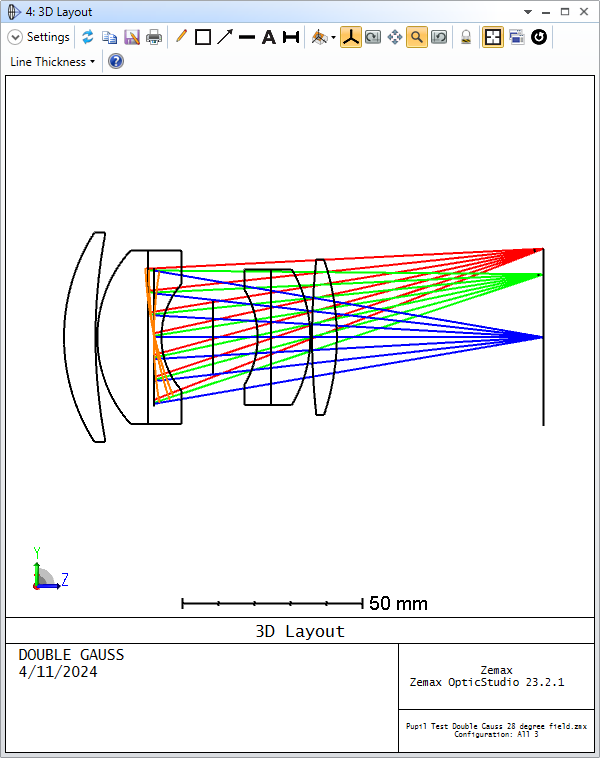
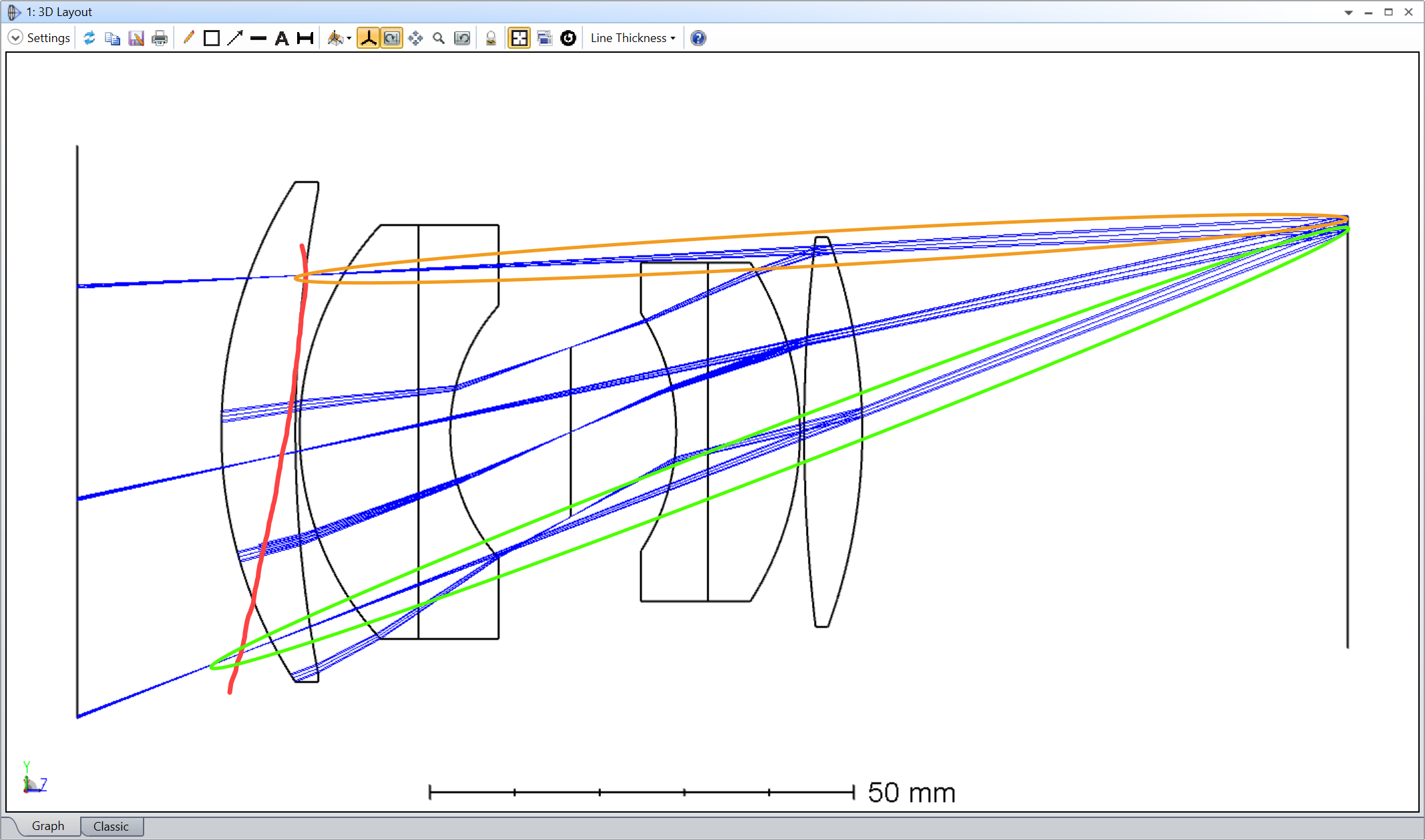
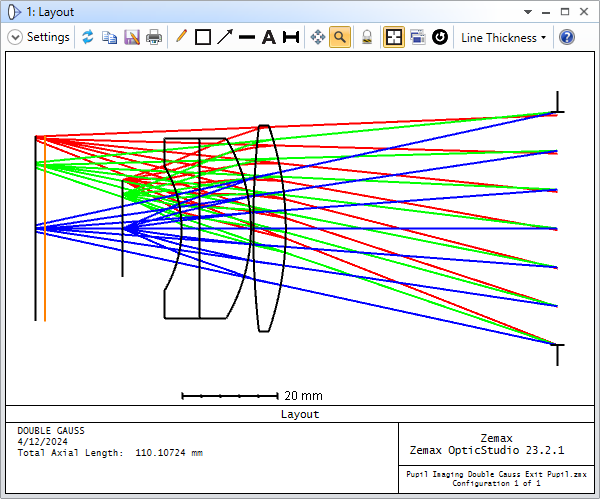
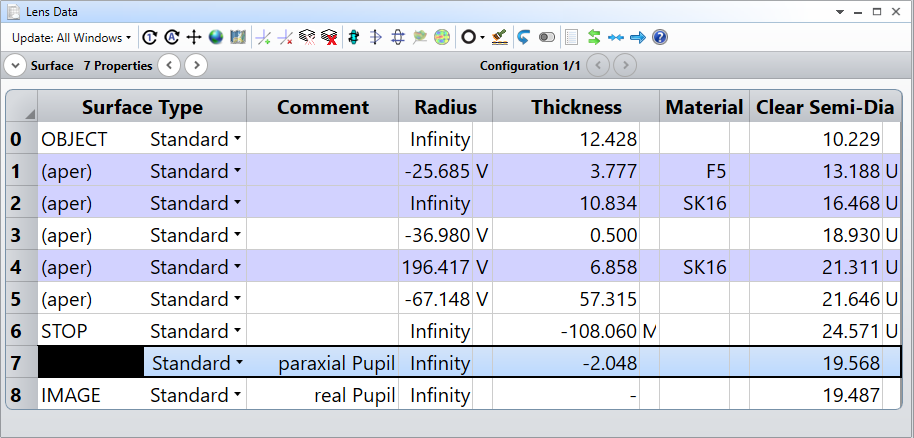
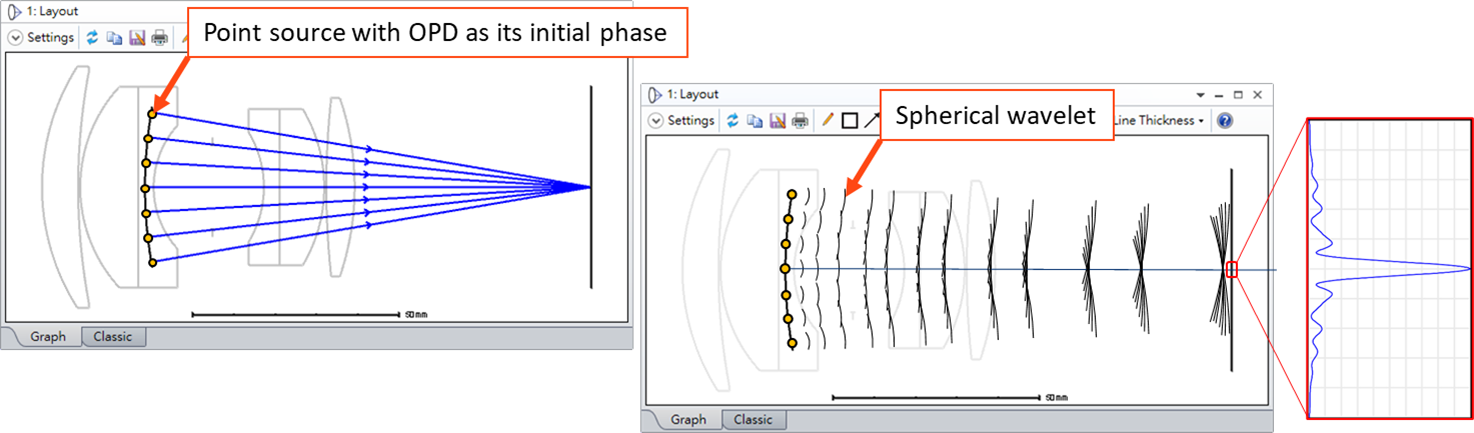
Hey Zemax team,
Sadly my license for OS does not include the new ‘draw entrance and exit pupils’ feature, but I saw a posting on LinkedIn that leads me to think it’s not correct. https://www.linkedin.com/posts/ir-ekim-yildirim-bb9481161_did-you-know-that-zemax-2024-r1-can-draw-activity-7179440511521292288-86_4?utm_source=share&utm_medium=member_desktop
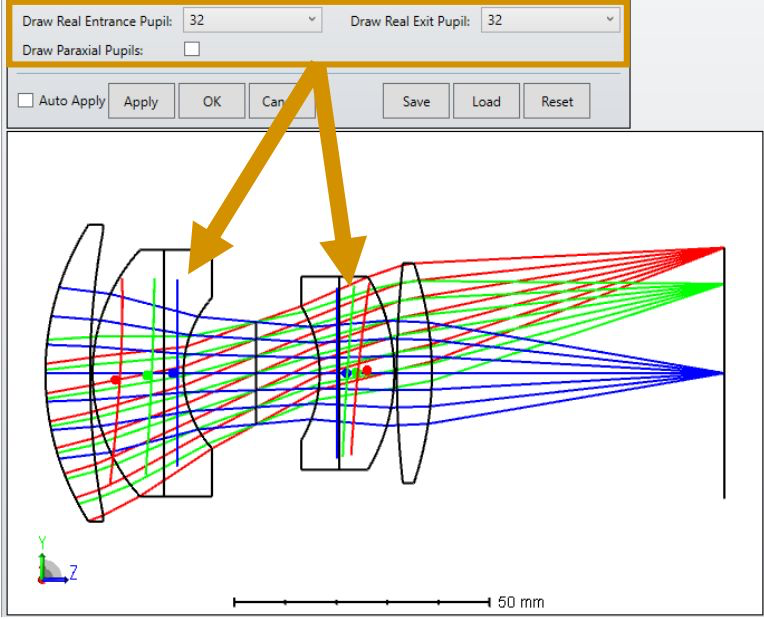
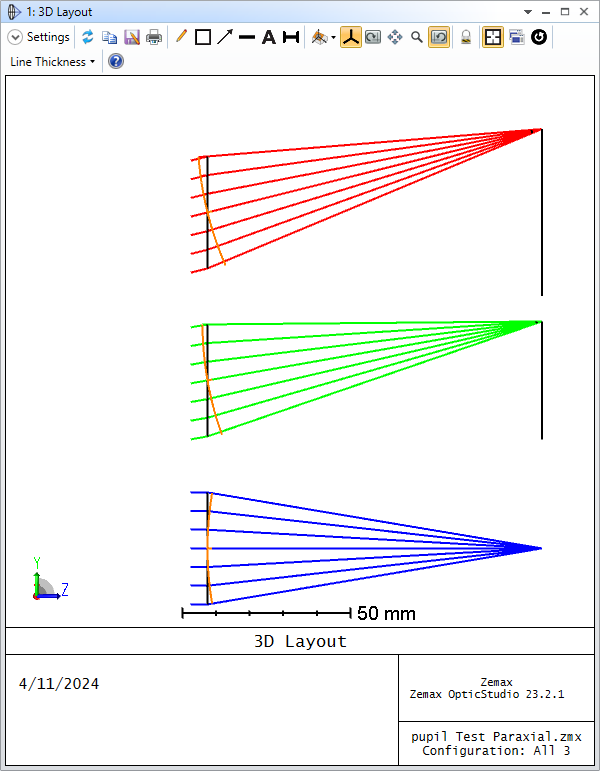
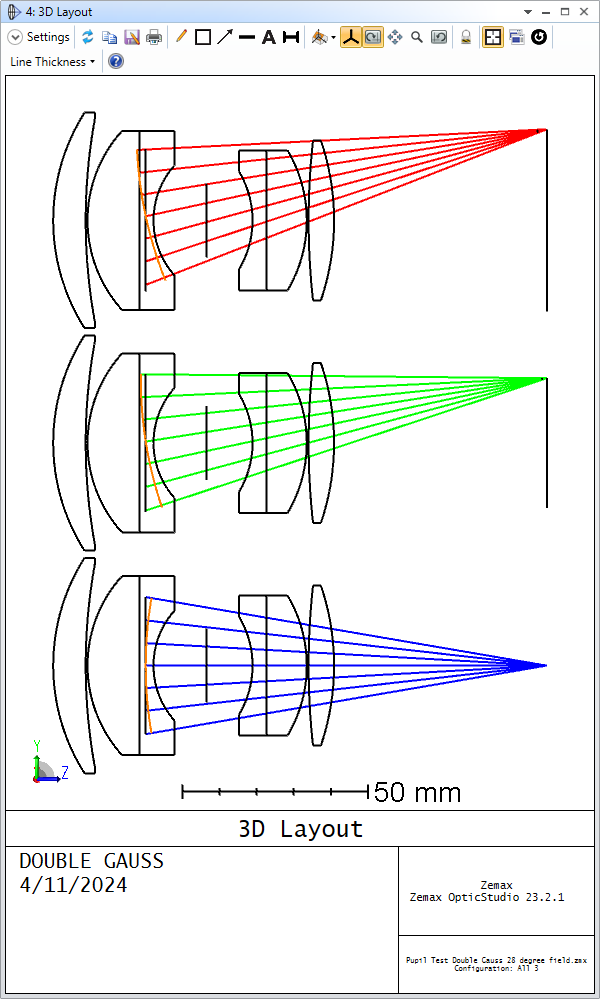
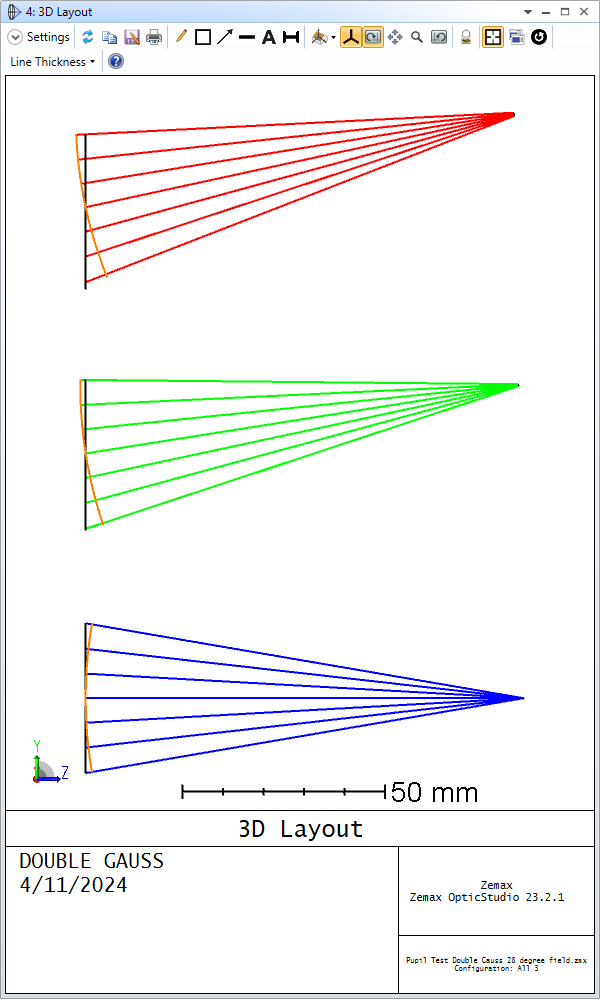
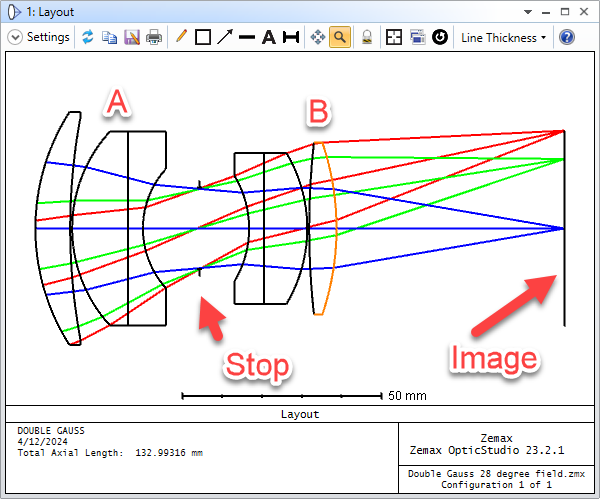
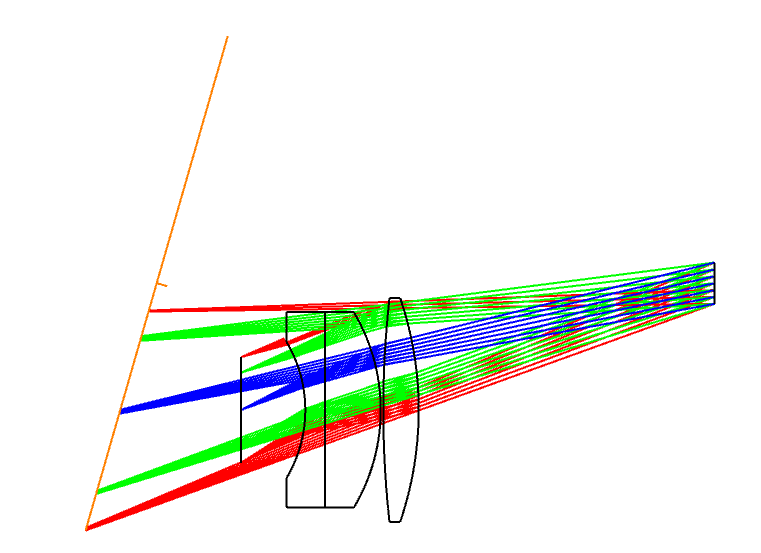
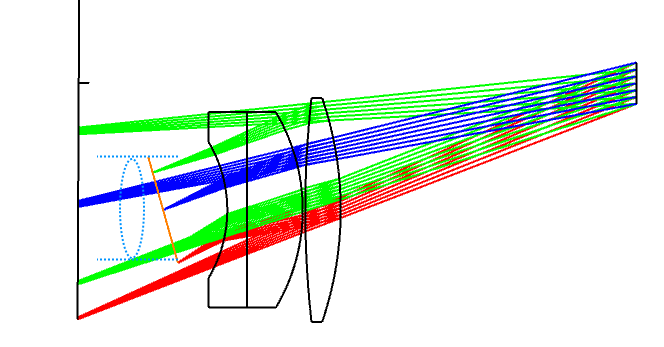
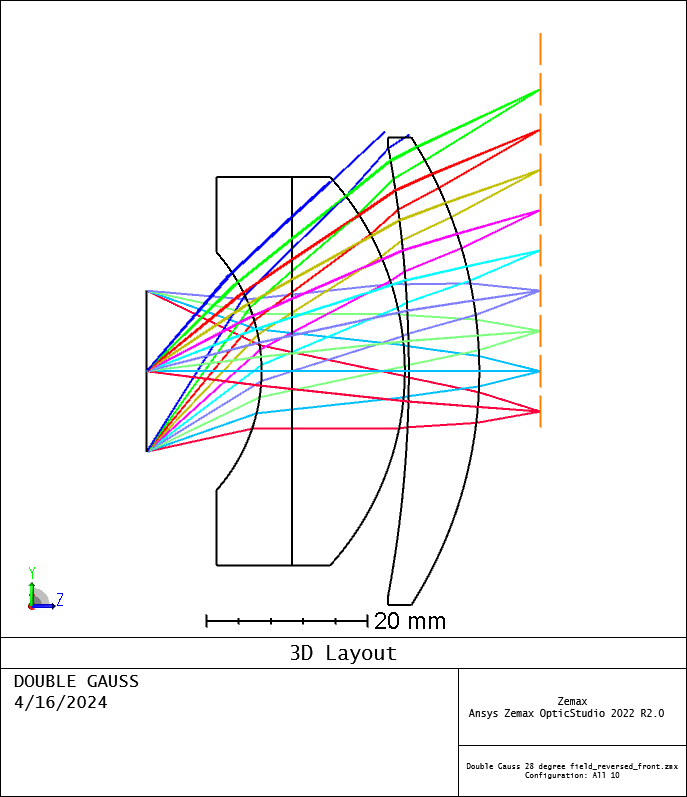
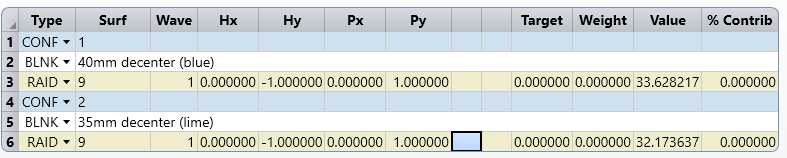
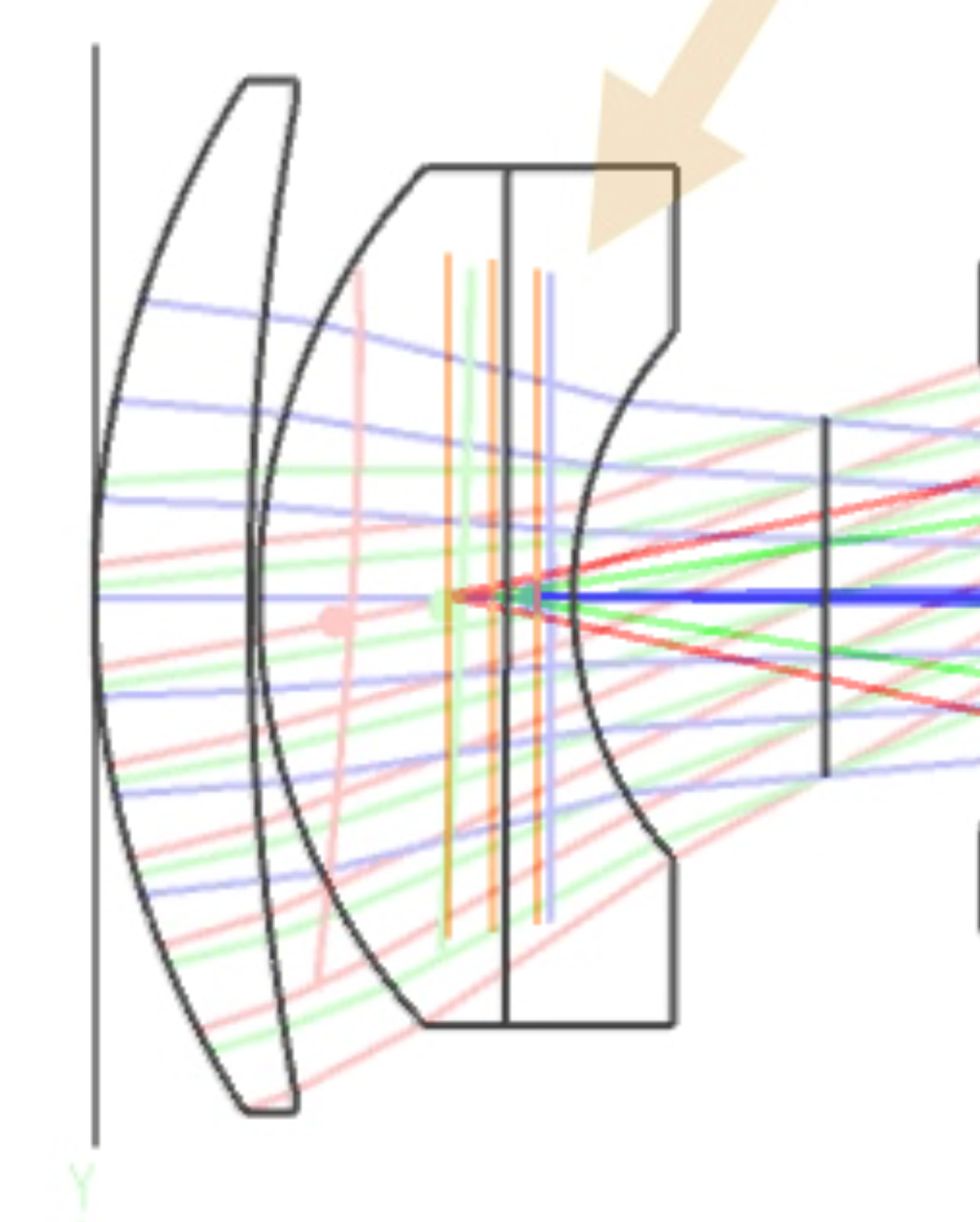
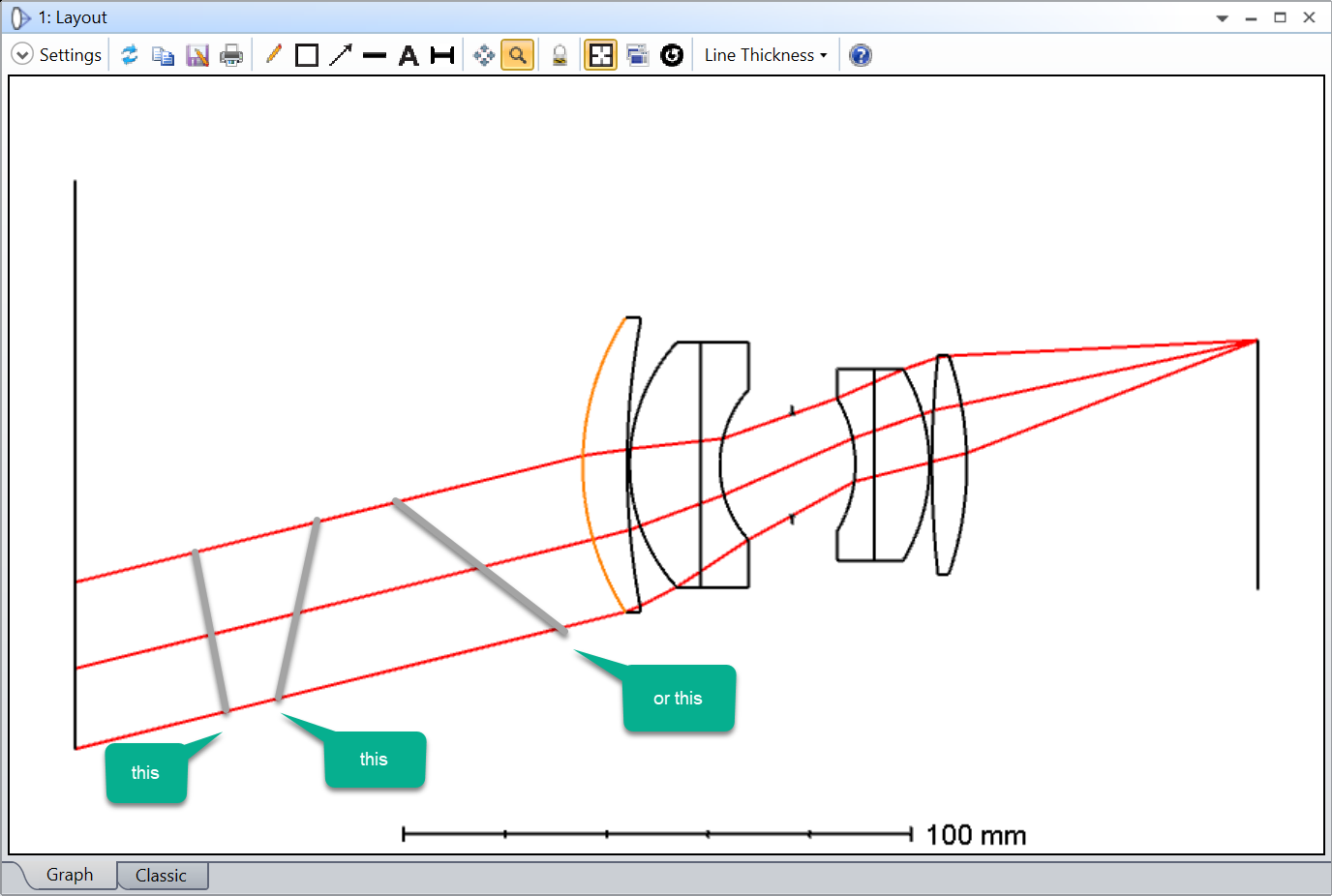
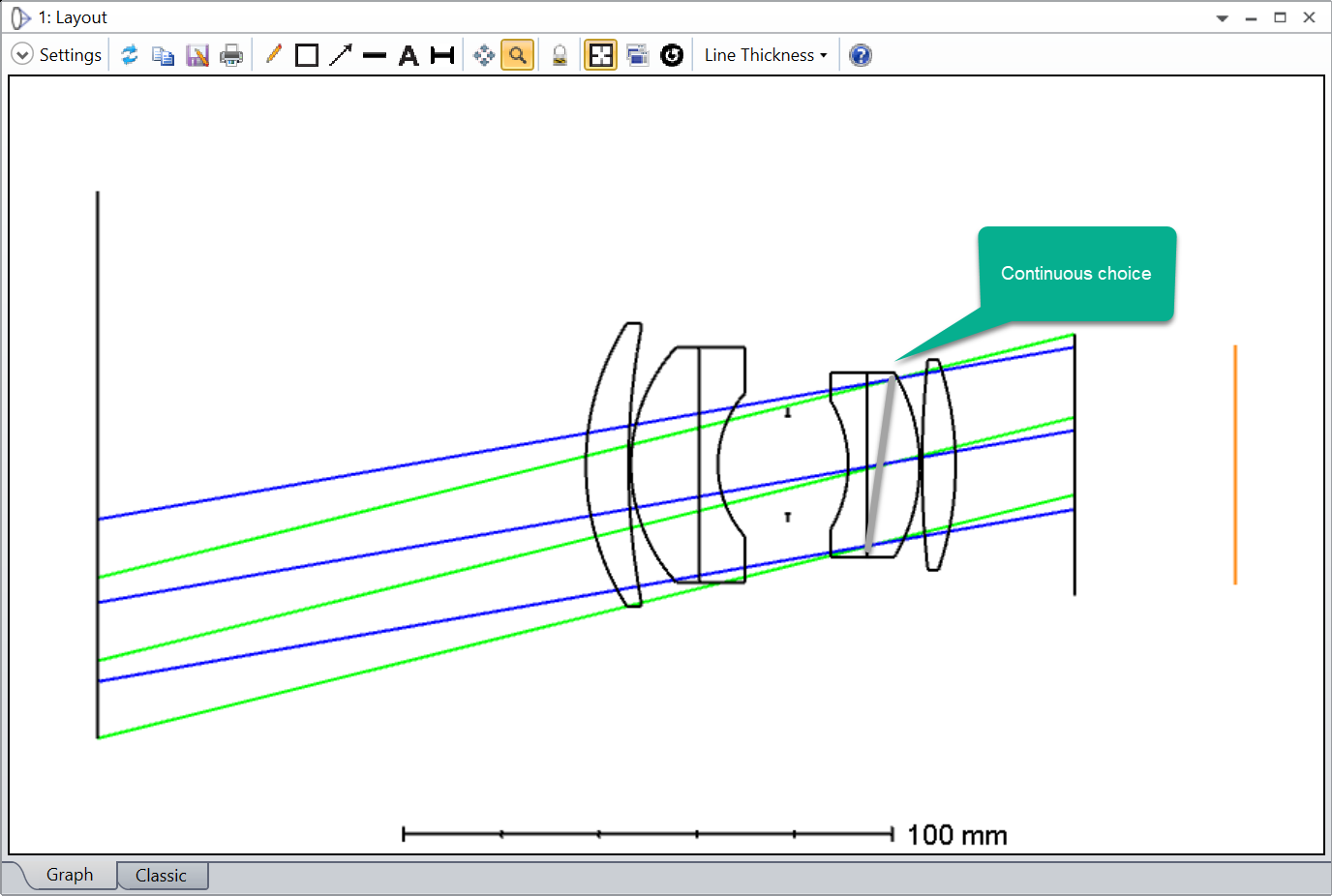
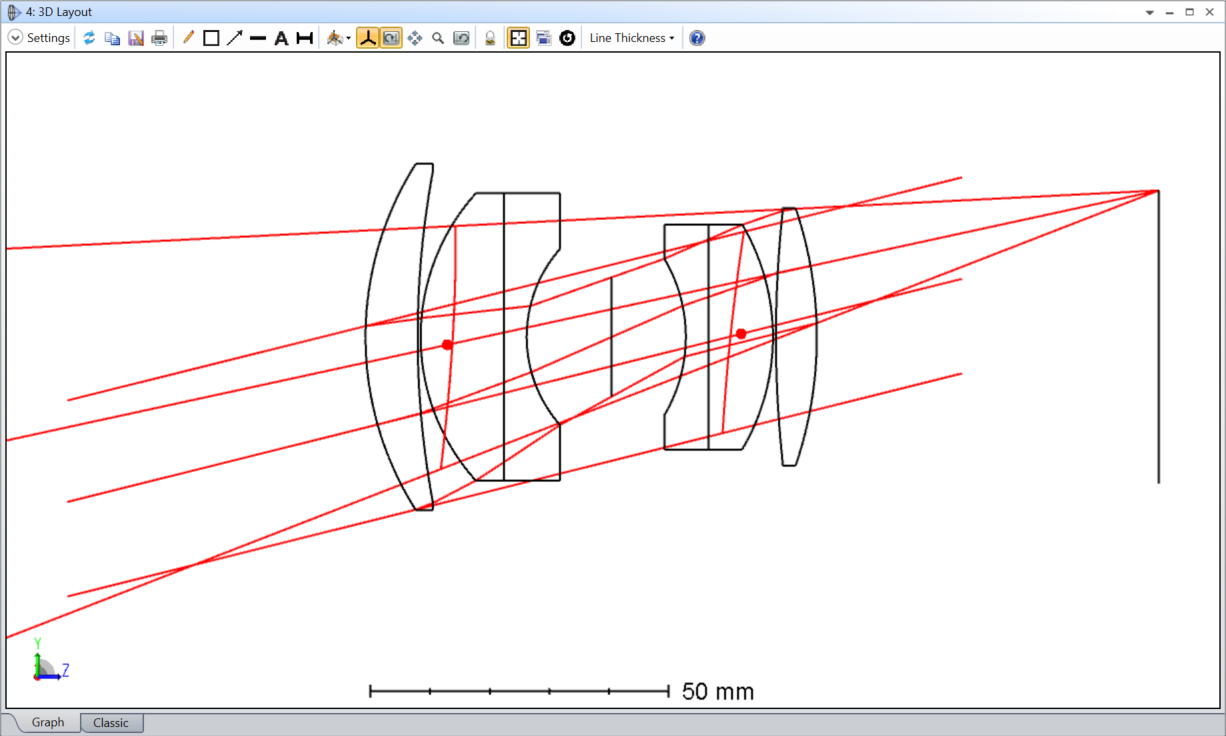
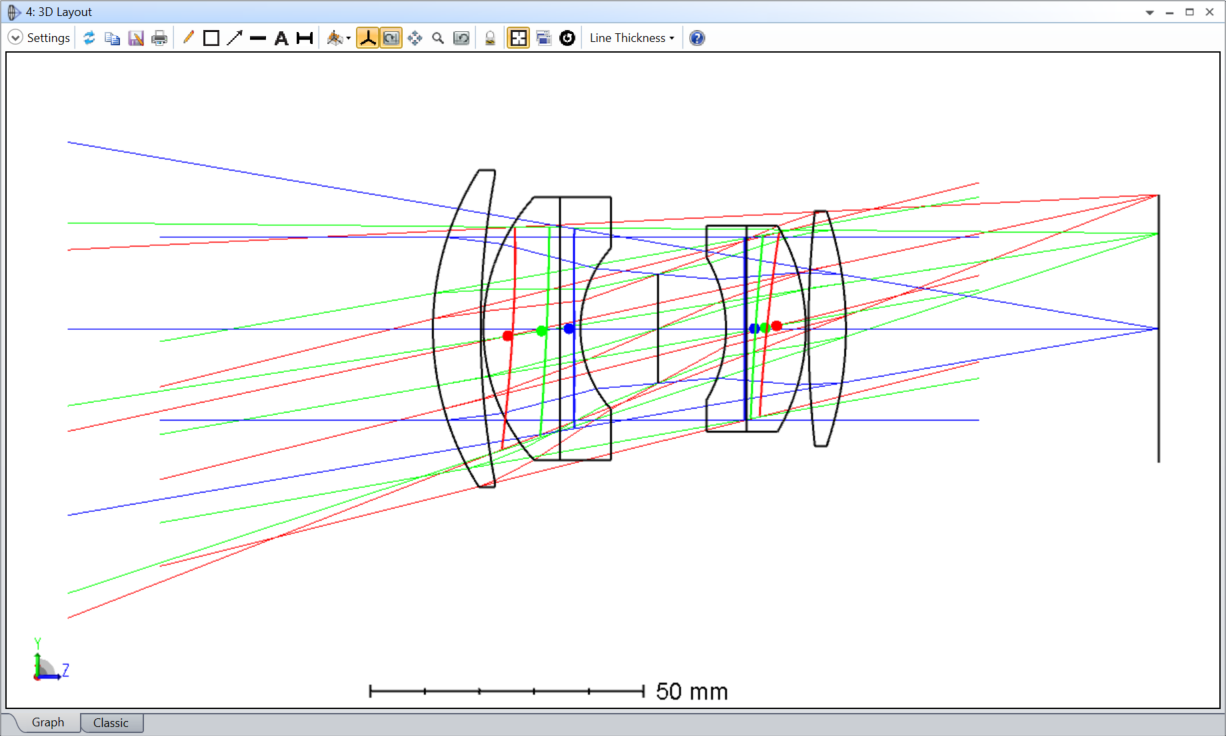
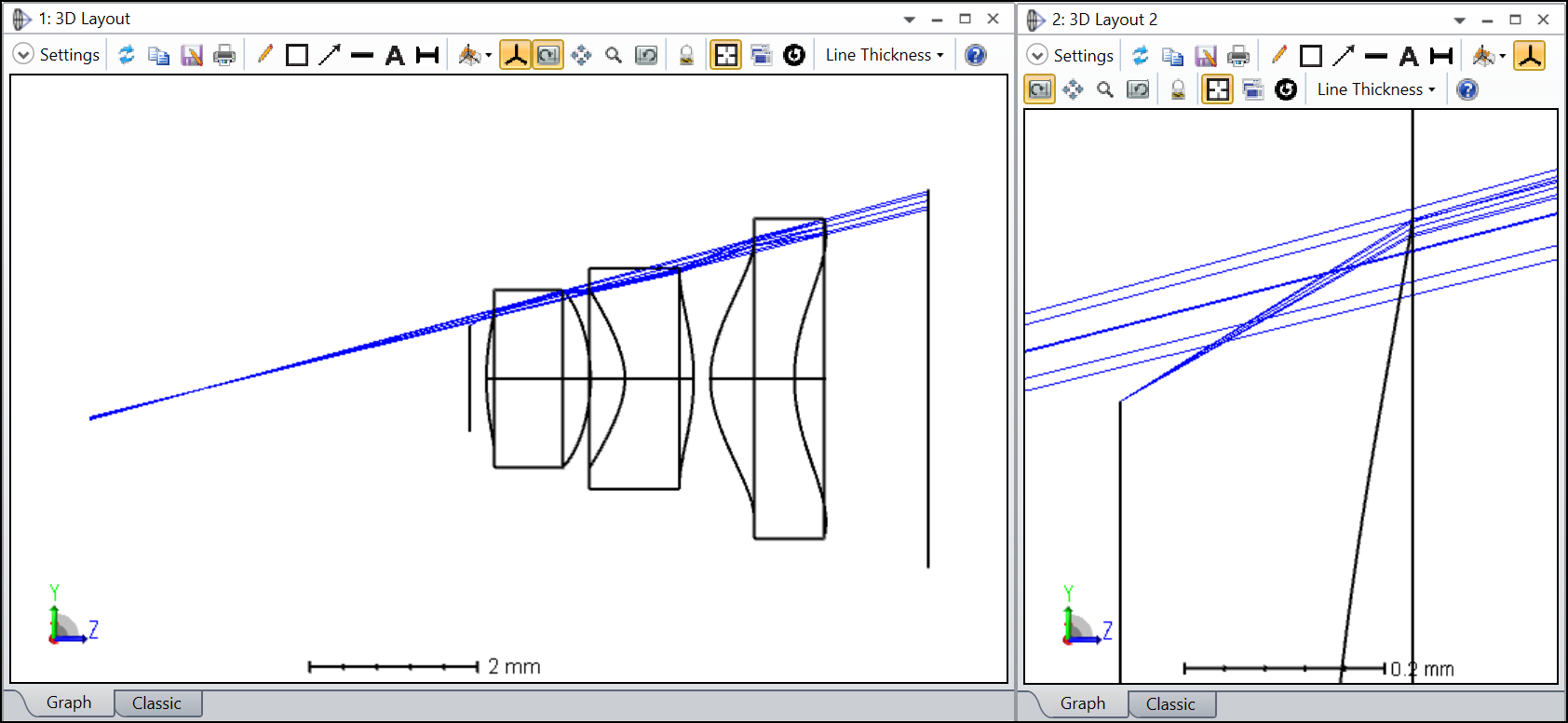
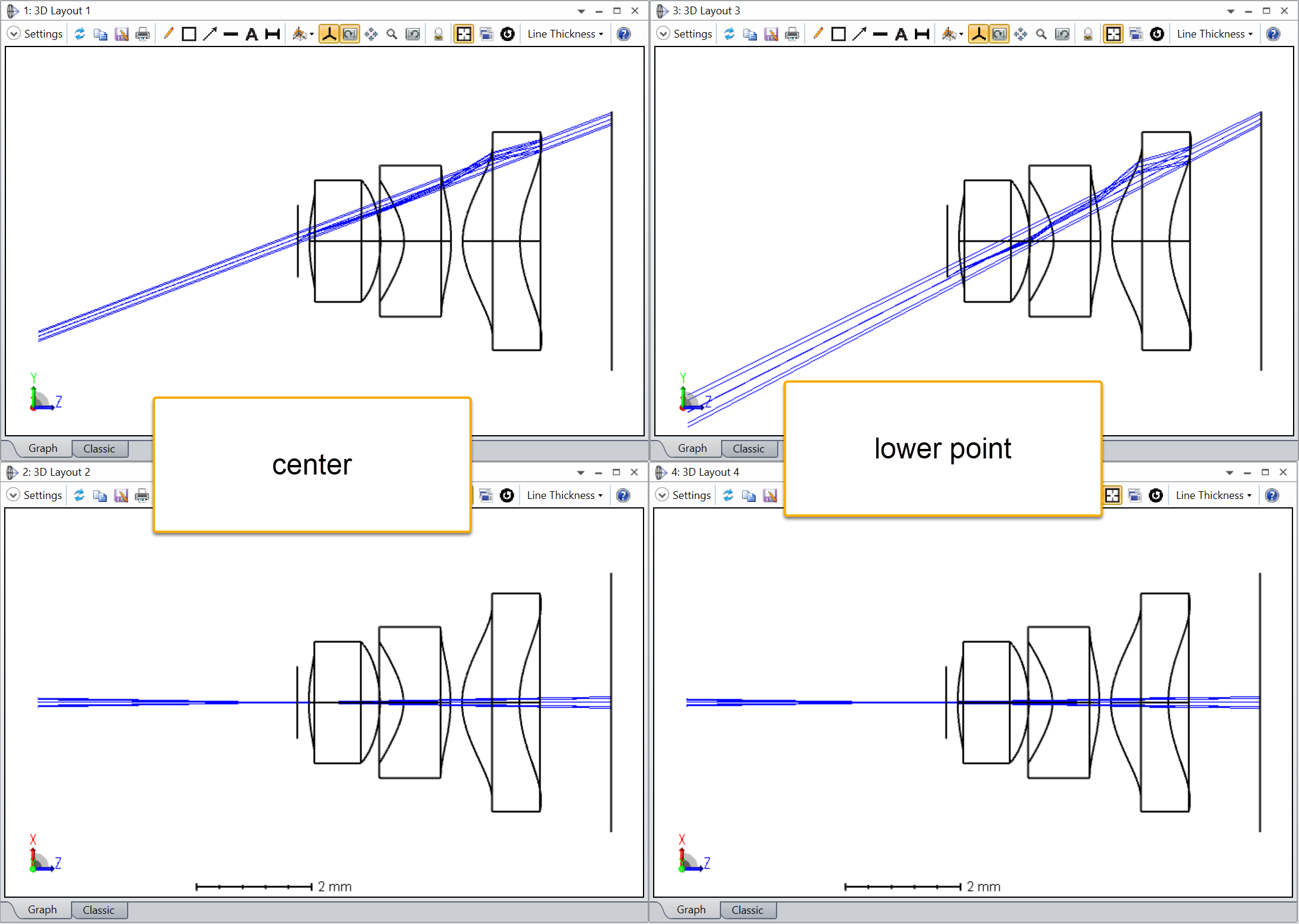
I’m assuming that the red pupils are the off-axis pupil (and so sees the red rays). The pupils appear to me to be:
- tilting the wrong way
- not centered on the chief ray of the field point
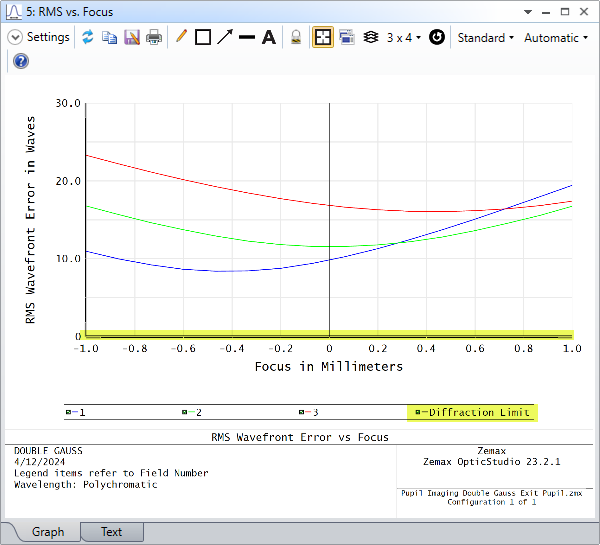
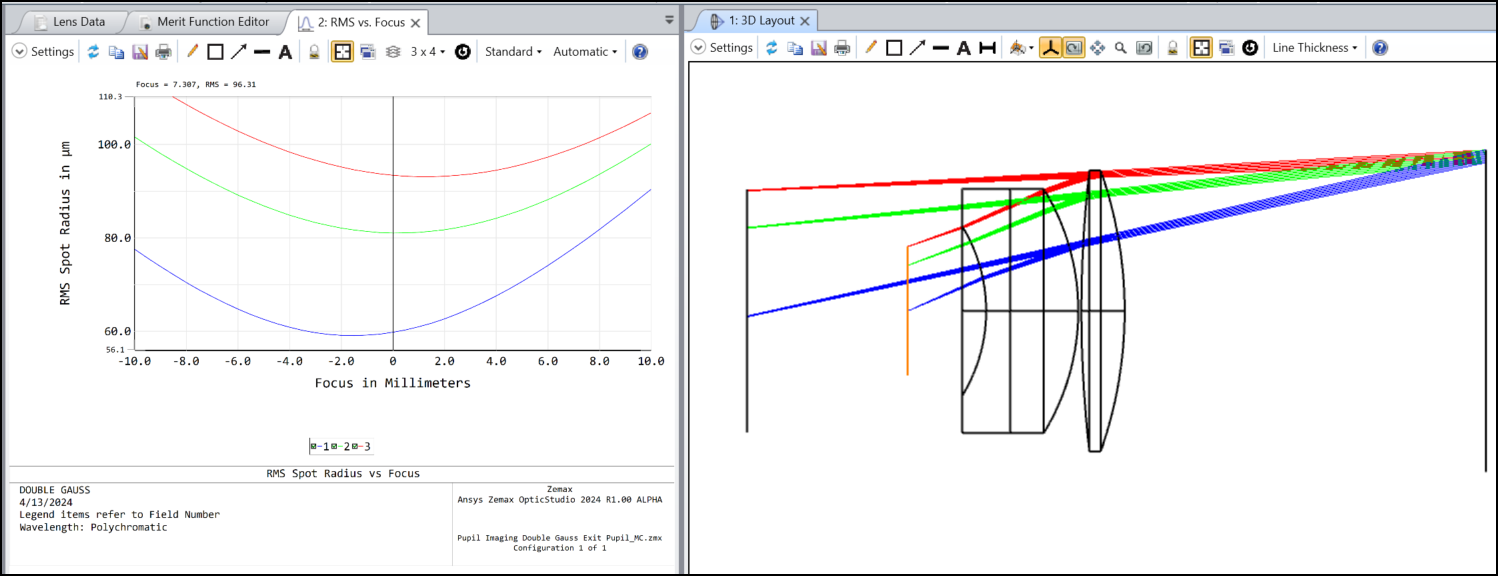
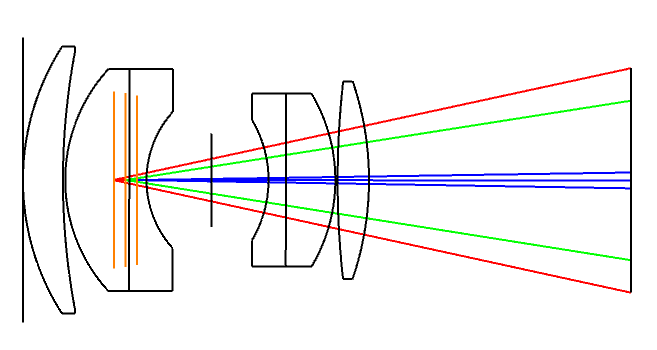
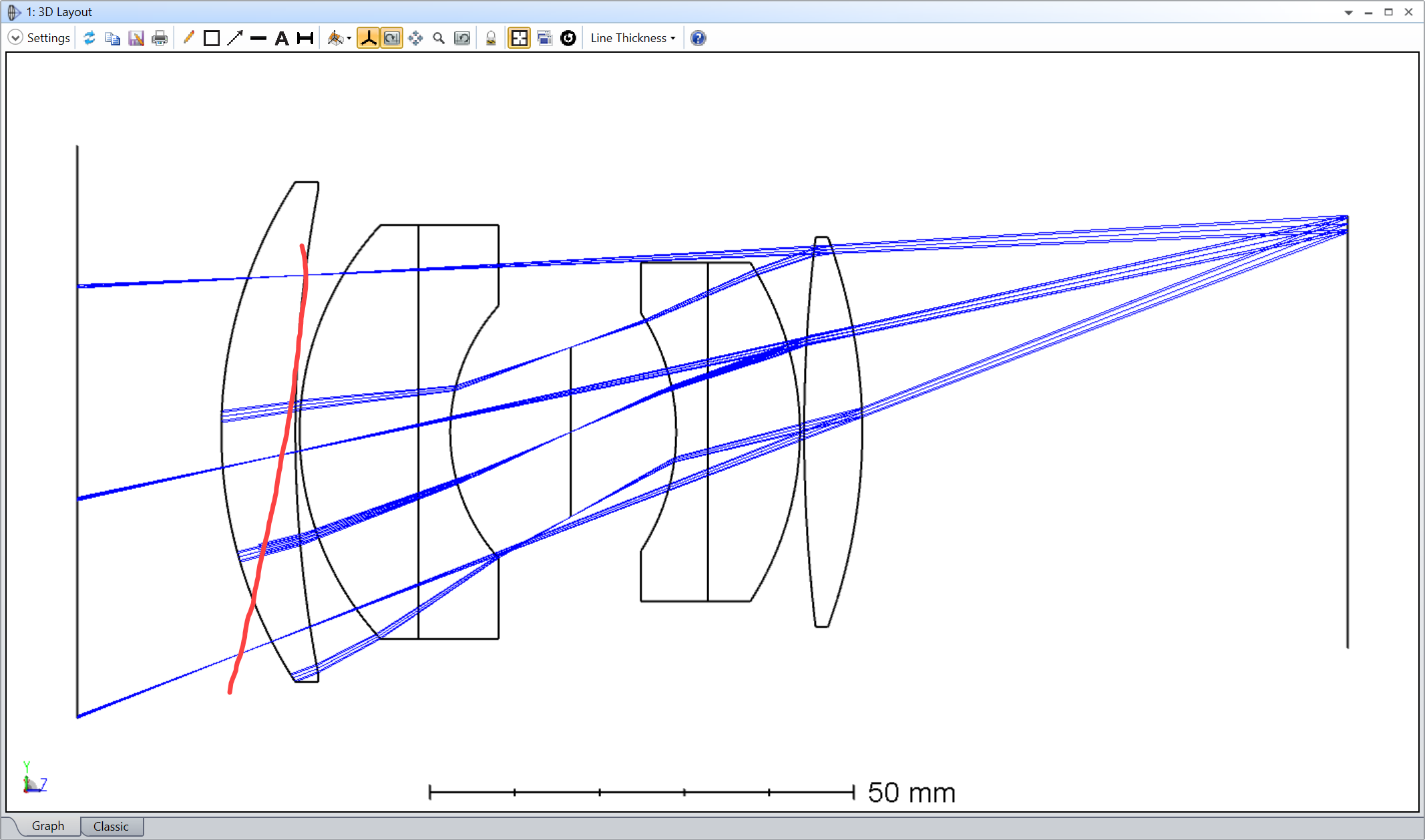
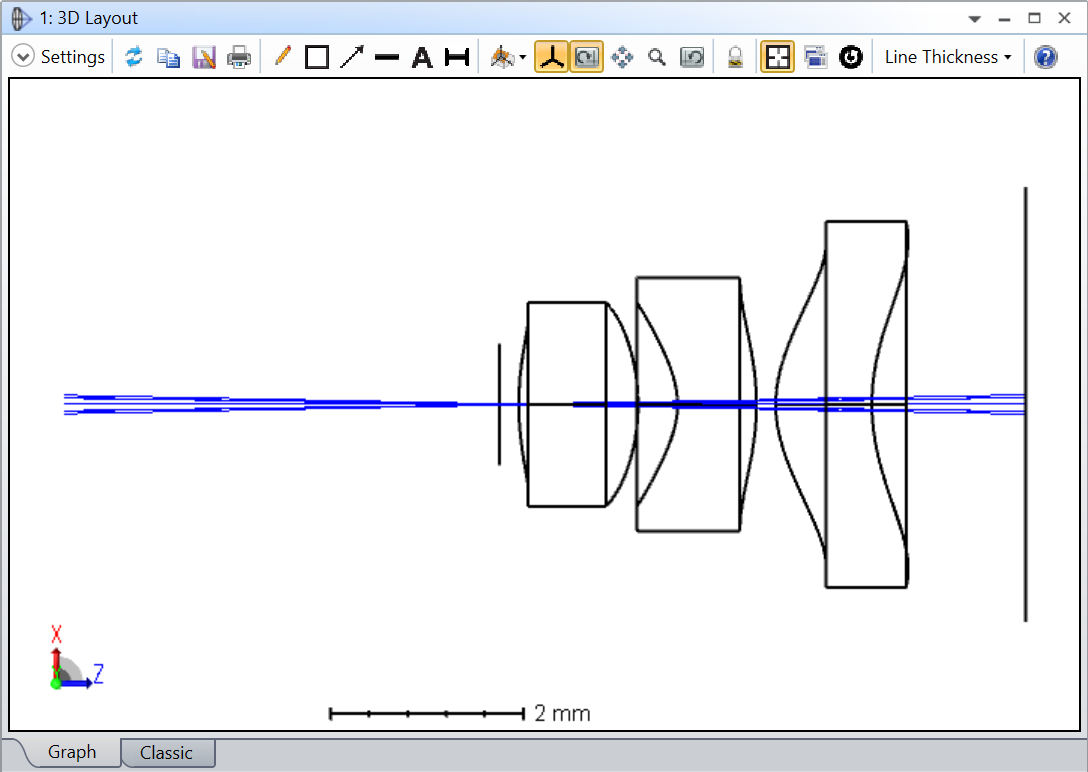
I can’t play with the feature to satisfy myself. Could someone post this layout (its the double Gauss sample file) with ‘Draw Marginal and Chief Rays’ selected please?
- Mark



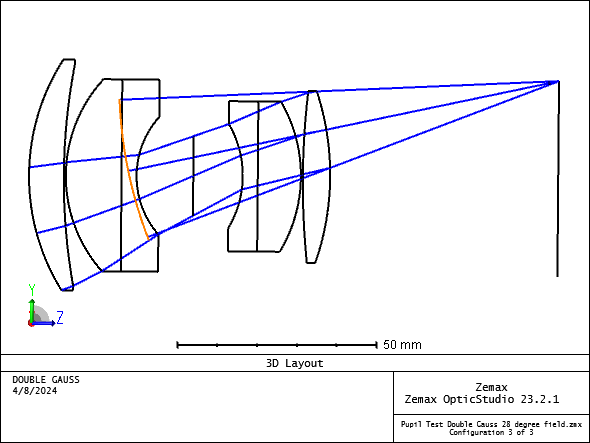
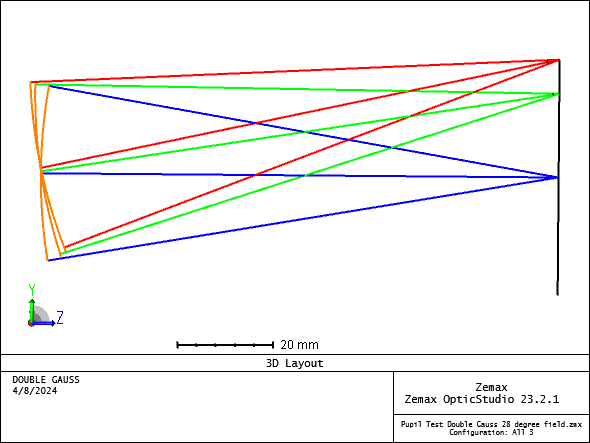




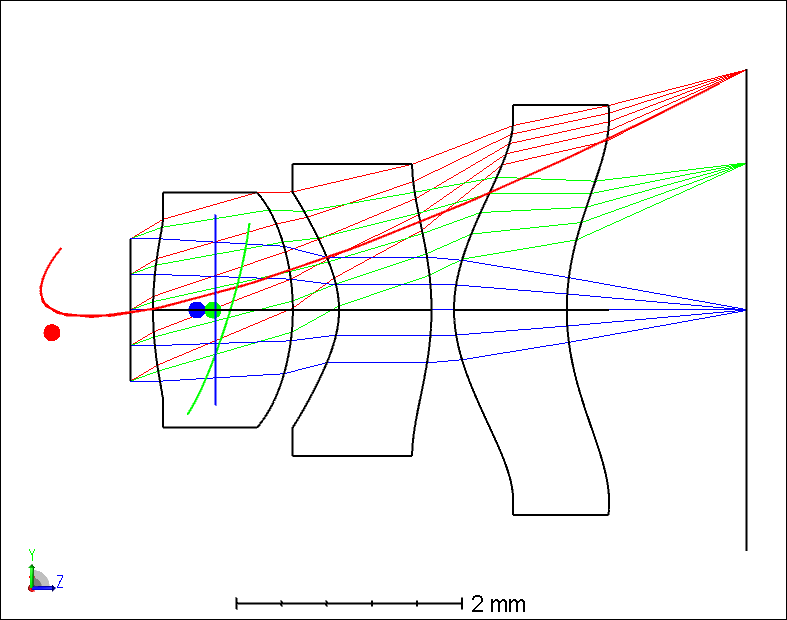

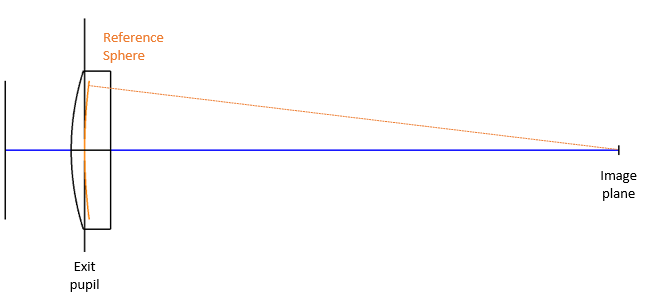

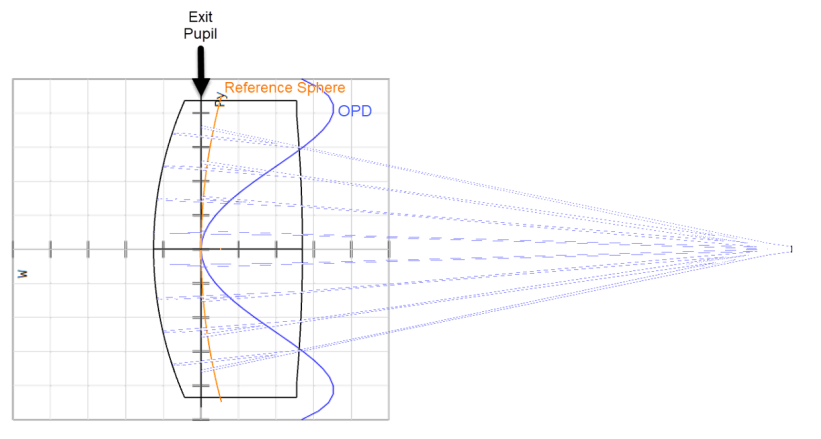
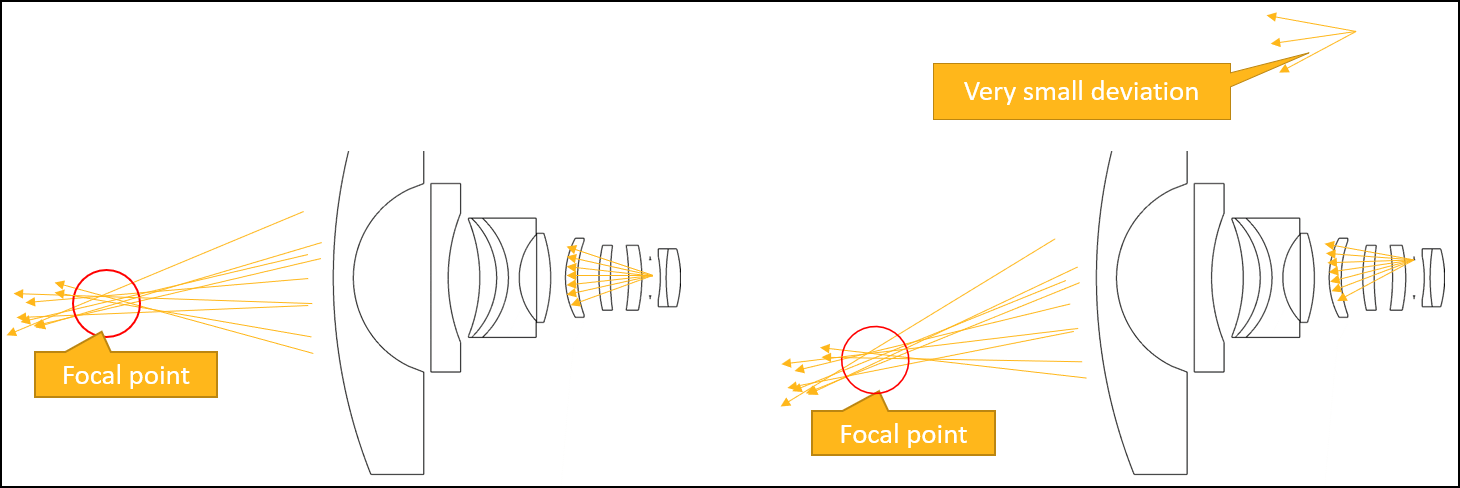
 The additional path length due to the tracing of the ray backwards to the exit pupil, subtracted from the radius of the reference sphere, yields a slight adjustment of the OPD called the “correction term”. This computation is correct and is the desired method for all cases of practical interest.
The additional path length due to the tracing of the ray backwards to the exit pupil, subtracted from the radius of the reference sphere, yields a slight adjustment of the OPD called the “correction term”. This computation is correct and is the desired method for all cases of practical interest.