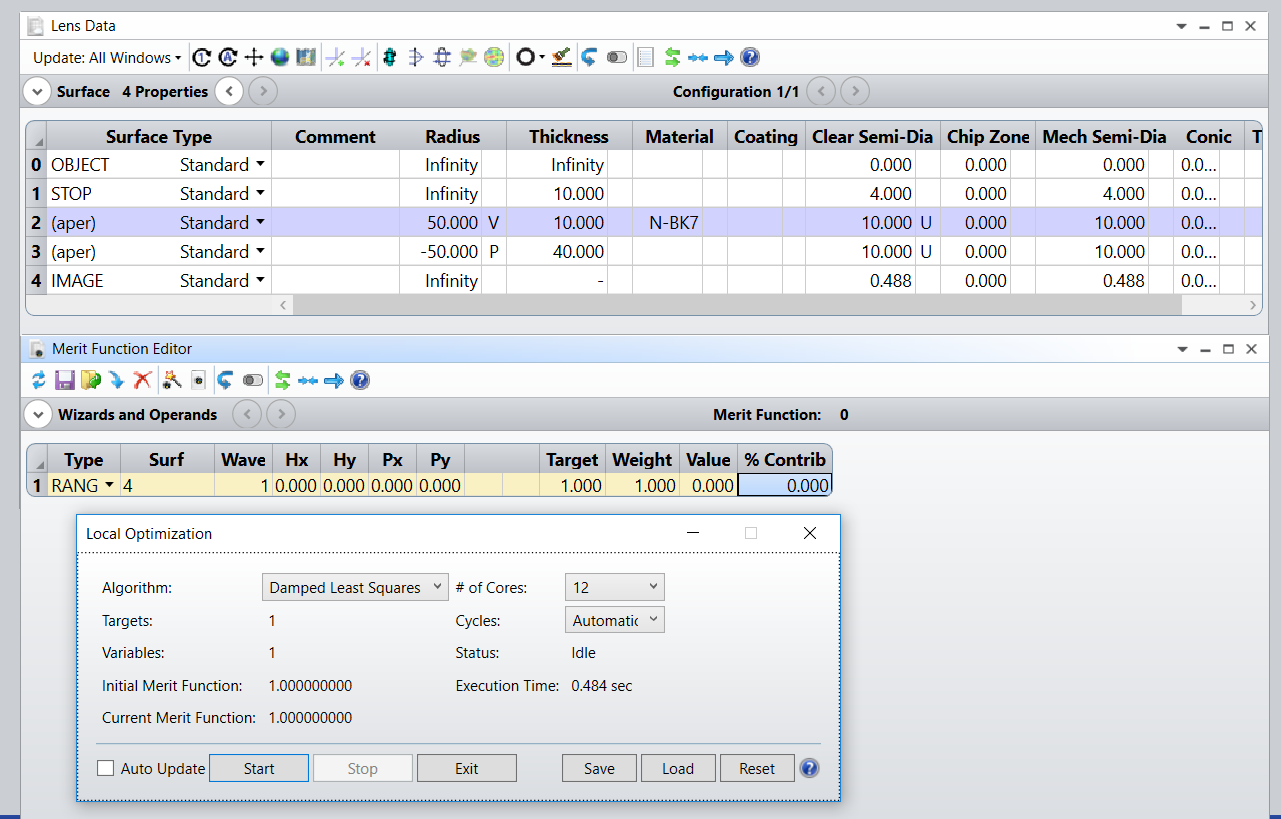
Hello, I’m trying to learn how the merit function definitions work. I went through a tutorial on it (https://support.zemax.com/hc/en-us/articles/1500005490261) and thought I understood how it worked, but when I try to implement something similar to what they used in the tutorial, the merit function does not compute the value and it is unable to optimize.
Additionally for the merit function types I don’t know what the codes mean exactly. is there some place to find this information? I tried the help (?) with no success.