I have no idea! What are you trying to achieve? _M

@kot_letova:

The number you are calculating should be related to the total optical power contained in the PSF.  I don’t know about the specific value you have, but here are my thoughts.

If you have a diffraction-limited system with a circular exit pupil, the intensity PSF is a jinc^2 function, where the first zero occurs at the Airy radius.  Typically it is normalized to a central intensity of one.  It’s straightforward to calculate the volume under this function evaluated using normalized transverse spatial coordinates (x/r0, y/r0) where r0 is the Airy disk radius.  Doing so makes the first zero occur at r/r0 = 0.61.

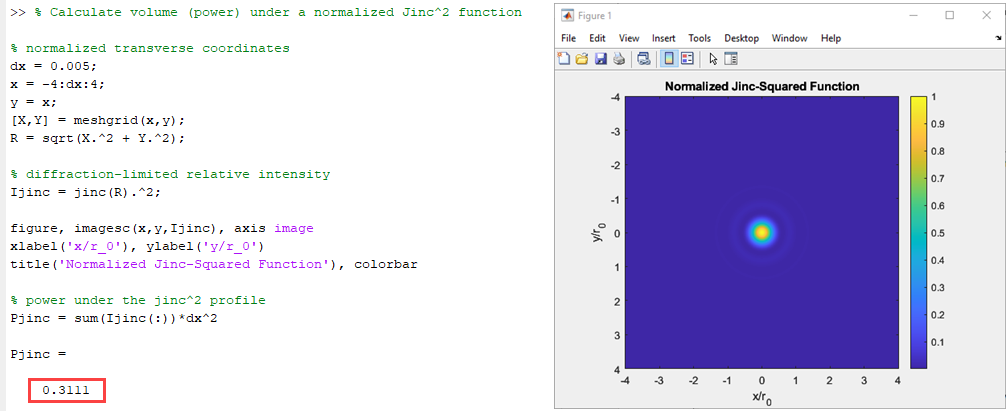
The value of the volume under this profile is 0.311 -- this represents a “normalized power.”

Now take a simple paraxial focusing lens in OpticStudio and evaluate the Huygens PSF. 

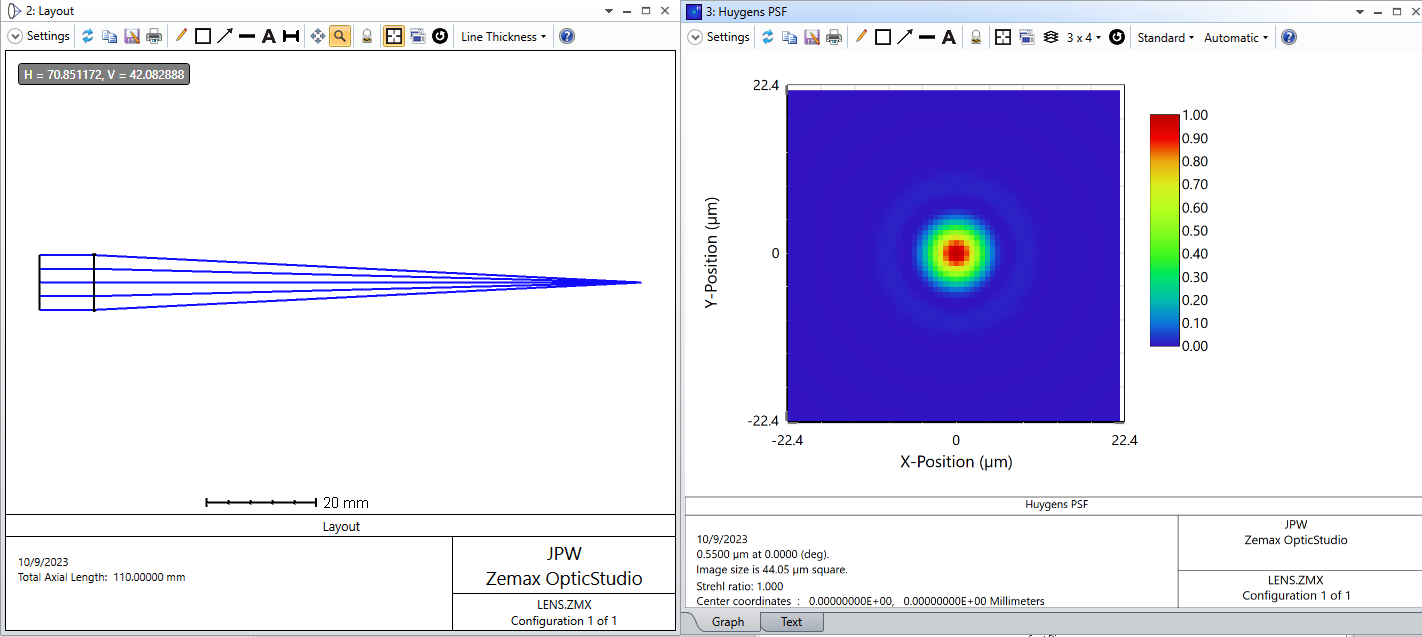
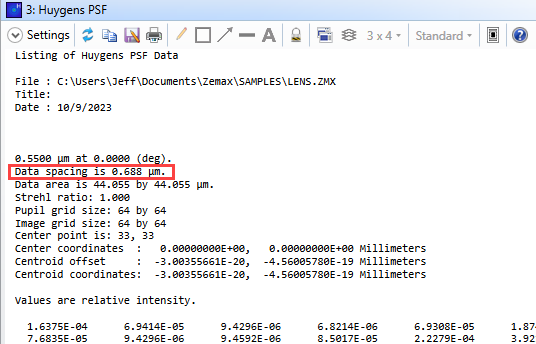
For 64x64 image sampling, the data spacing is 0.688 um.

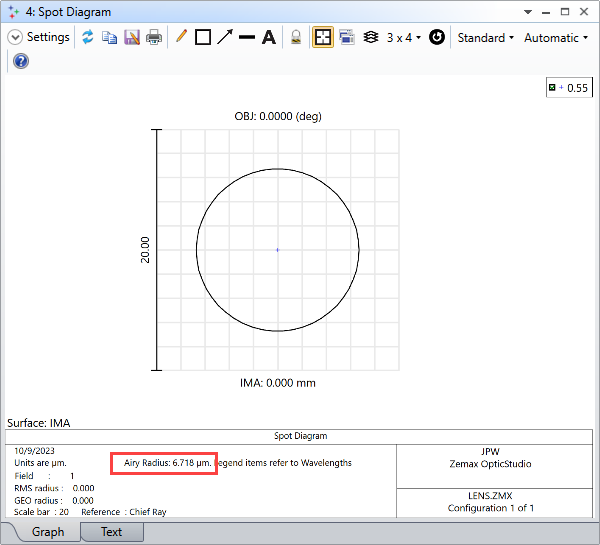
Also, the Airy disk radius for this example is 6.718 um.

Now, let’s sum the relative intensity pixel values of the Huygens PSF, and multiply by an appropriately normalized pixel area (0.61*dx/r0)^2:

As expected, the value comes out the same as previously calculated.

If aberrations are present, the PSF will broaden and it’s peak value will be less than one (i.e., the Strehl ratio), but the total power should remain the same. 

If the exit pupil has Gaussian apodization, then the diffraction-limited PSF will be Gaussian and the “normalized power” contained in the PSF should be somewhat different (but I haven’t tried testing this case).

Hope this makes sense.

Regards,

Jeff

@Jeff.Wilde thank you for the answer! It is not exactly what I want, but it pushed me to some interesting thoughts