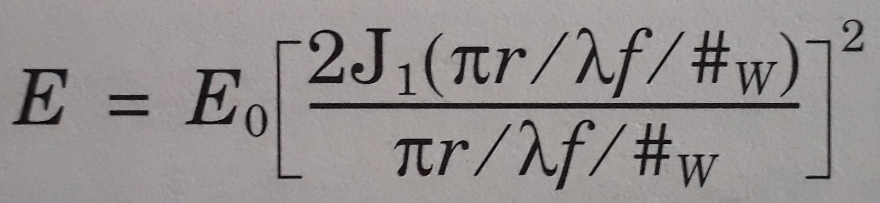Hi John!
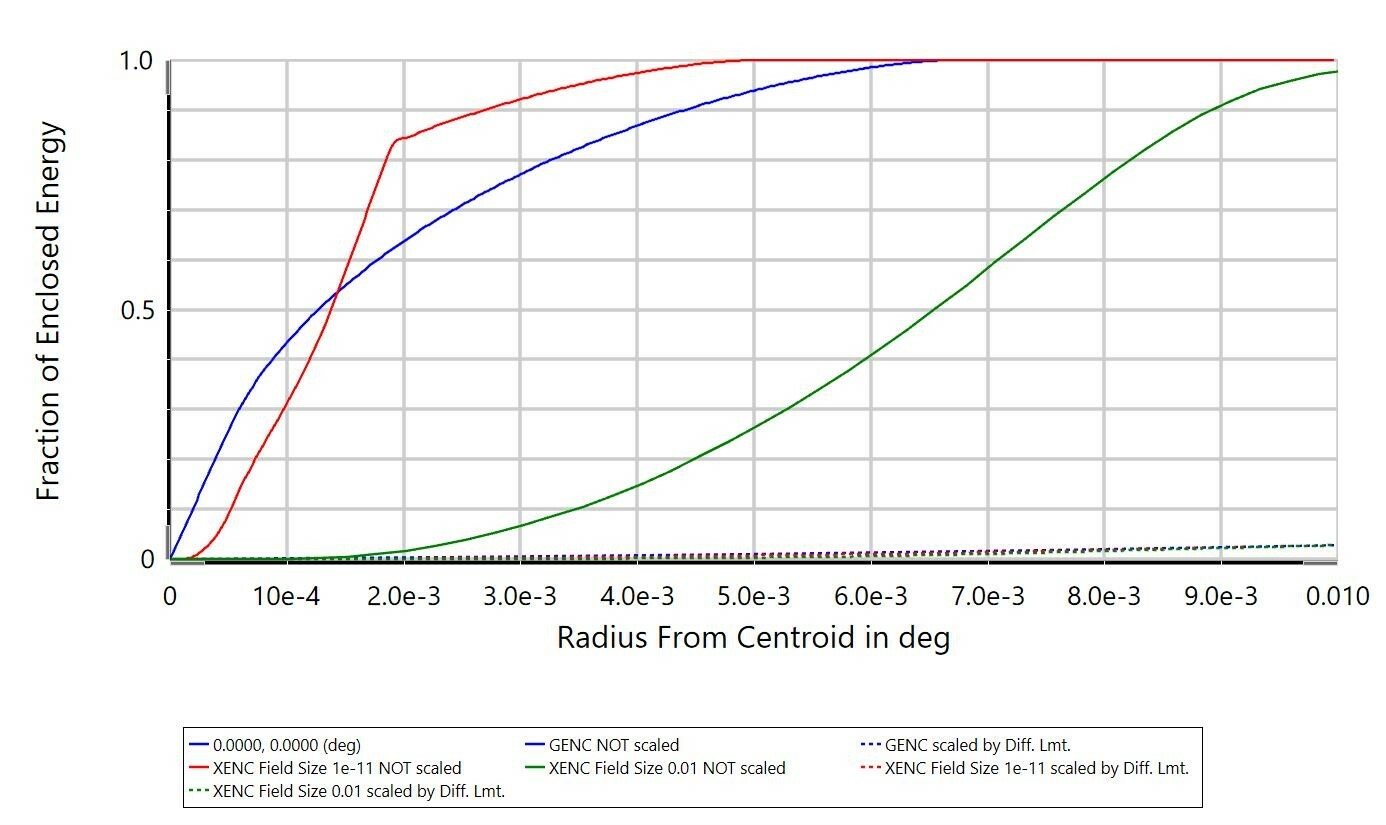
The Extended Source Encircled Energy analysis obtains results in a very similar manner to the Geometric Image Analysis tool. In both, you effectively select an IMA file for OpticStudio to generate rays from. You specify the size of the IMA file in object space and what field point the file is centered on. The difference is that Geometric Image Analysis will show the simulated image after tracing rays through your optical system, whereas the Extended Source Encircled Energy reports the fraction of energy that is arriving on your image plane as you go away from the centroid (or other reference point) of the simulated image:
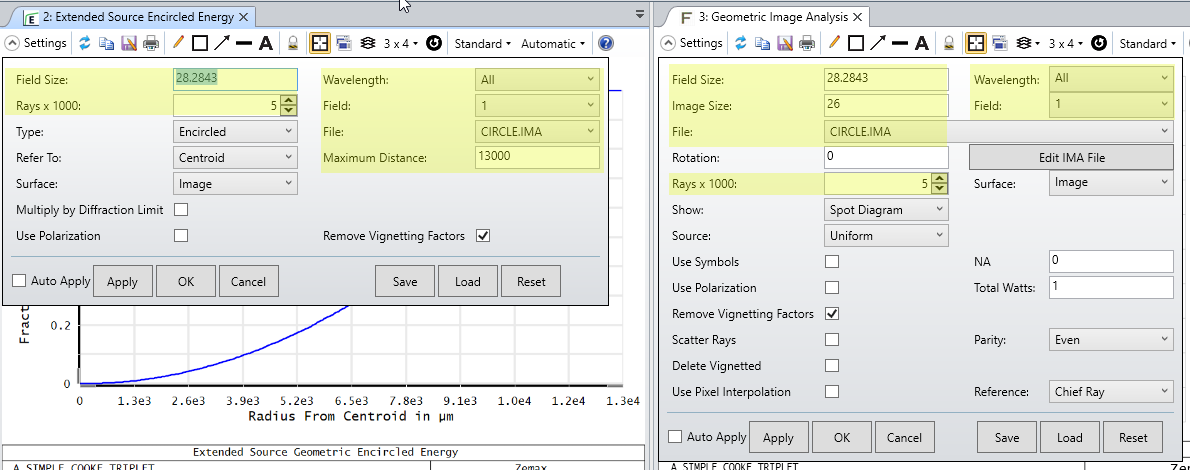
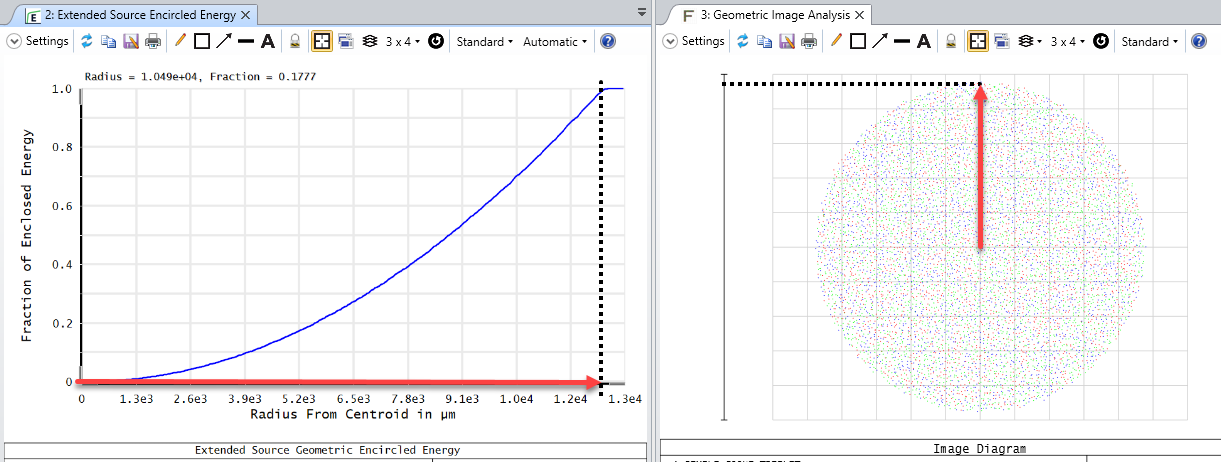
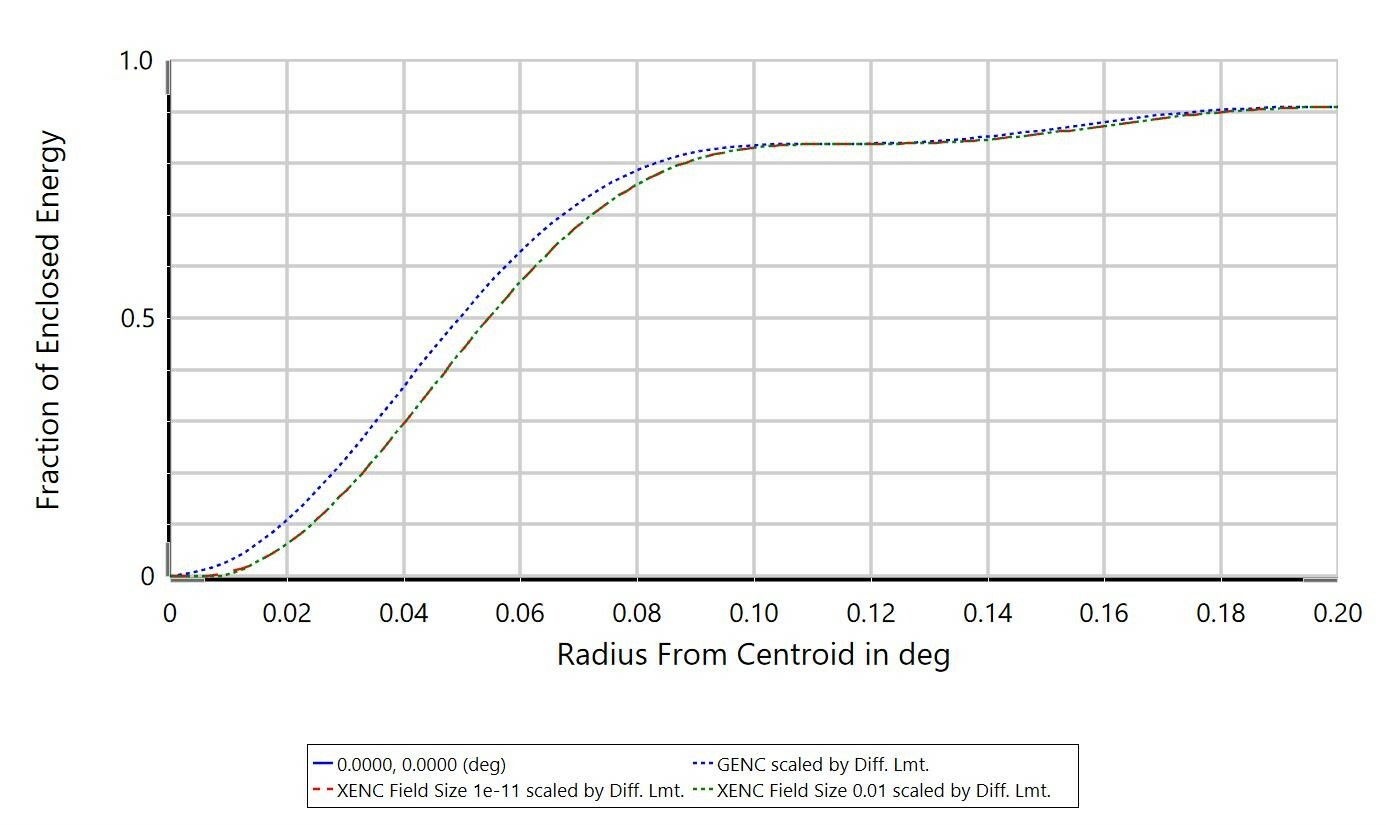
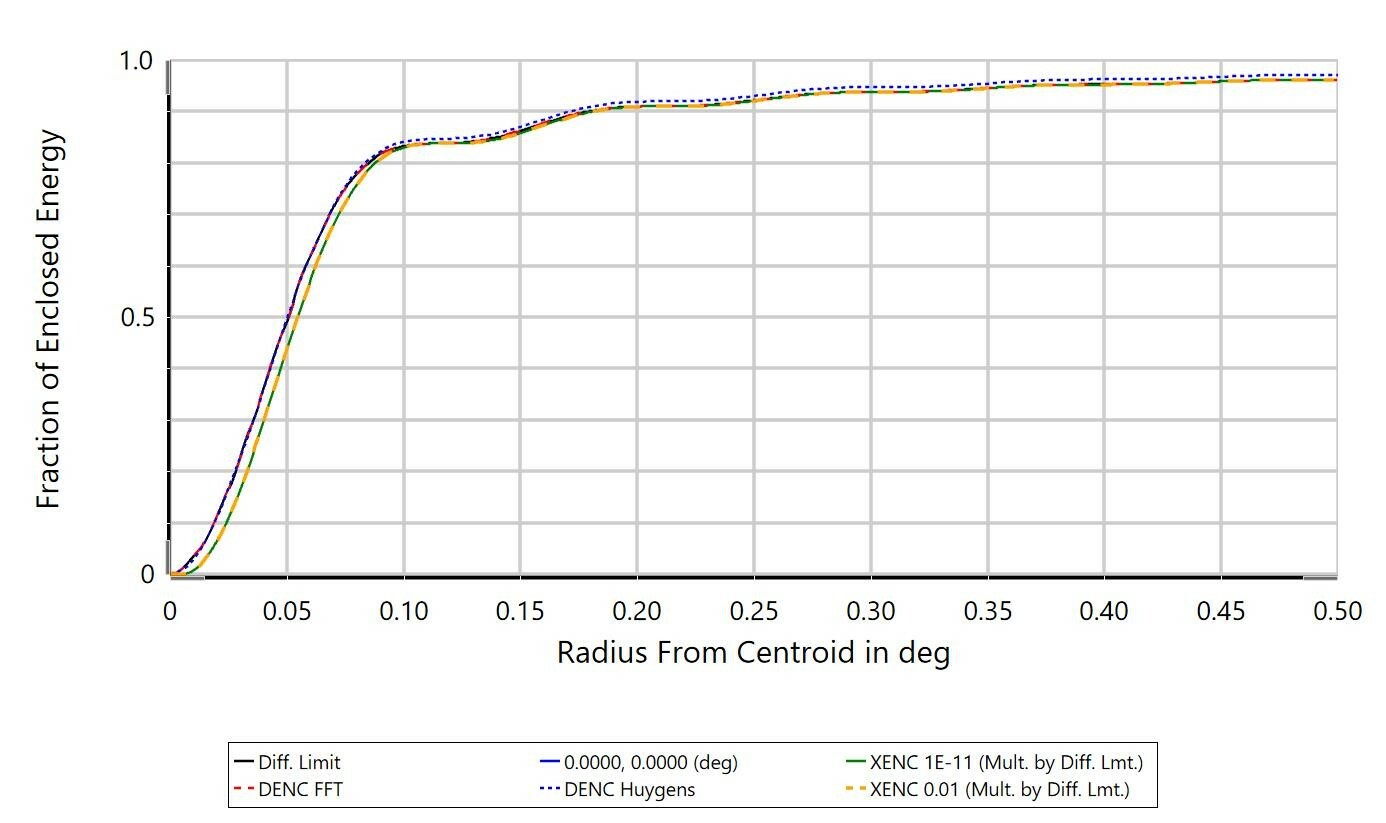
The differences between Extended Source Encircled Energy and the diffraction-based computation Diffraction Encircled Energy may come down to the optical system itself. In the Help Files, there is some discussion on the applicability of the 'Multiply by Diffraction Limit' setting (from 'The Analyze Tab (sequential ui mode) > Image Quality Group > Enclosed Energy > Extended Source'):

Let us know if you have any further questions here, or if anything else needs clarifying!
~ Angel