Hi all.
I want to display reference sphere on a layout plot.
Is it possible?
Then, could you tell me how can I do this?
Thanks in advance
Hi all.
I want to display reference sphere on a layout plot.
Is it possible?
Then, could you tell me how can I do this?
Thanks in advance
Best answer by Sandrine Auriol
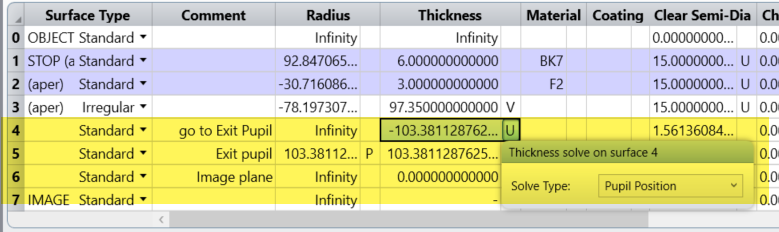
Sorry it is a bit of a late answer but by reference sphere, do you mean the reference sphere for the wavefront calculation?
If yes you can add two surfaces before the image plane. This will work for on-axis fields. For off-axis, you will need to add some coordinate breaks.
Sandrine
Enter your E-mail address. We'll send you an e-mail with instructions to reset your password.