This question comes up often. Siegman’s M^2 term measures the deviation of a Gaussian beam from the ideal case. It is vital to recognize that the M^2 is a measure, not a parameter. Think of it as analogous to the standard deviation of a data set. There are unlimited ways to get the same measure. For a Gaussian Beam, scaling the beam size and divergence values by the value of M will produce a beam quality factor of M^2, but this is merely one way to do this. The Paraxial Gaussian Beam tool does not have many degrees of freedom, so this makes sense, but it would be a disservice to have a generic M^2 parameter for POP beams because it can mean anything.

The issue can be easily demonstrated by looking at a couple ways to generate the same M^2 from a starting Gaussian Beam in POP. The attachment to this post contains an arbitrary sample system and a POP tool. Initially, the beam is slightly focused and brought to an image surface well before focus.

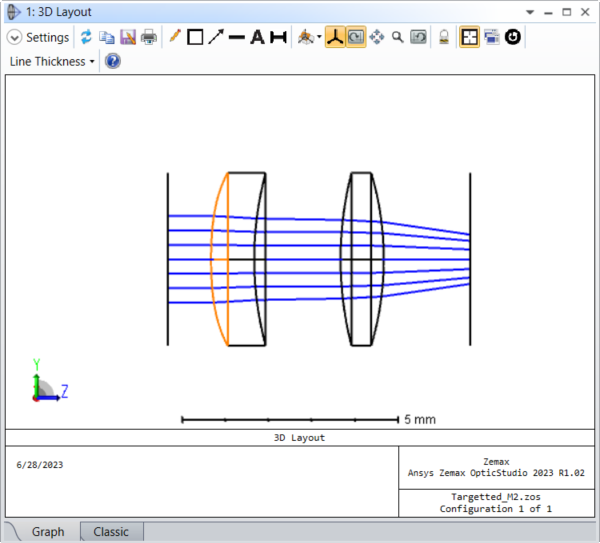
We can begin by making the fourth and sixth order terms for the Even and Odd Aspheres variable, for a total of four variables. A look at the Merit Function Editor shows that we are starting with a quality factor of 12.8 and are trying to create a beam with a factor of 20. The POPD operands impose this target measured in X and Y.

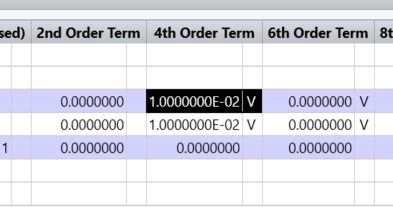
The initial beam is essentially Gaussian for all appearances.

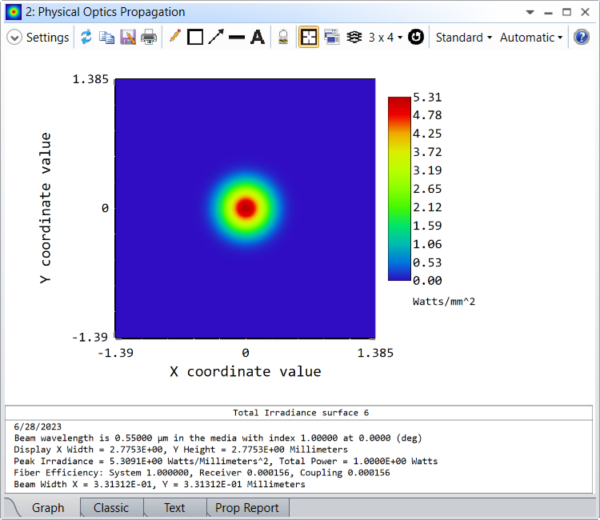
In a single cycle, the beam is shaped to an M^2 of 20 by shaping it to diverge strongly, creating a larger beam size as we can see:

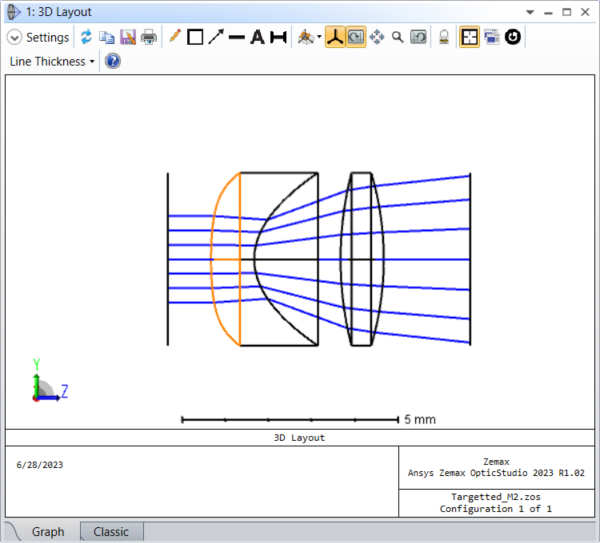
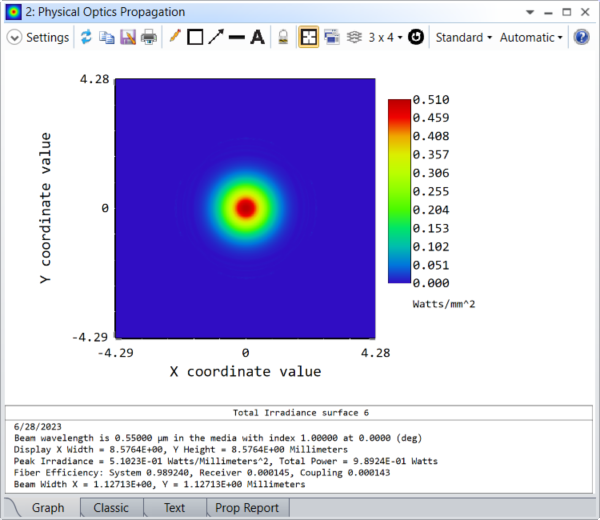
Undo these changes and remove the variable solves on the Aspheres. Now we can go to the Zernike Standard Sag surface and designate instead the terms Zernike 7 to Zernike 10 (parameters 21 to 24) as variable. Running the optimizer again to create a targeted quality factor of 20 yields these very different systems and beams:

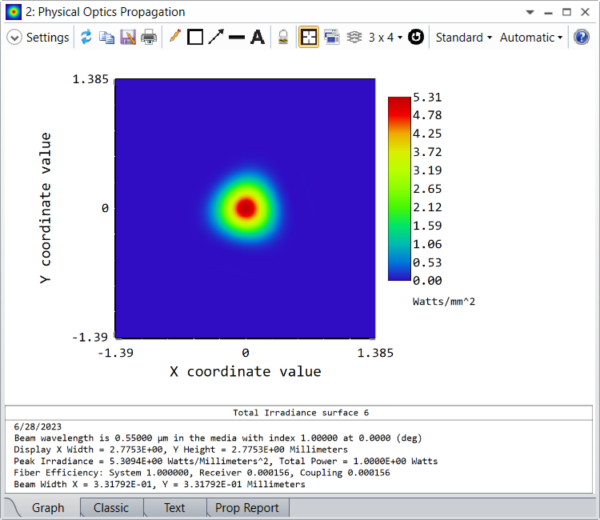
The second shaped beam, with a quality factor of 20, is now converging and not even radially symmetric.

This method of generating beams with a specific quality factor is not the ideal method. Even using the same variables, a different set of initial conditions could lead the optimization to produce a different result. The better way to get a beam with a specific value is to ask what about your initial beam is causing the deviation from the perfect Gaussian beam. If you have a source that comes from a manufacturer, you may be able to get a beam file (.ZBF) with the initial beam stored and ready to go. Options like the DLL are also available for users that wish to specify the beam pixel by pixel.

For a quick-and-dirty initial beam with a specific M^2, this field shaping approach may be viable, but remember always that you are not creating a unique beam in this way.