Hi all,
I’m not going to create a repository for this, but if you quickly need a modulo operator in your Merit Function, there you have it. Hx and Hy are the operand numbers (integer) that will be used as the numerator and denominator respectively.
The relevant part of the code is self-explanatory (hopefully):
int numerator = (int)TheApplication.OperandArgument1;
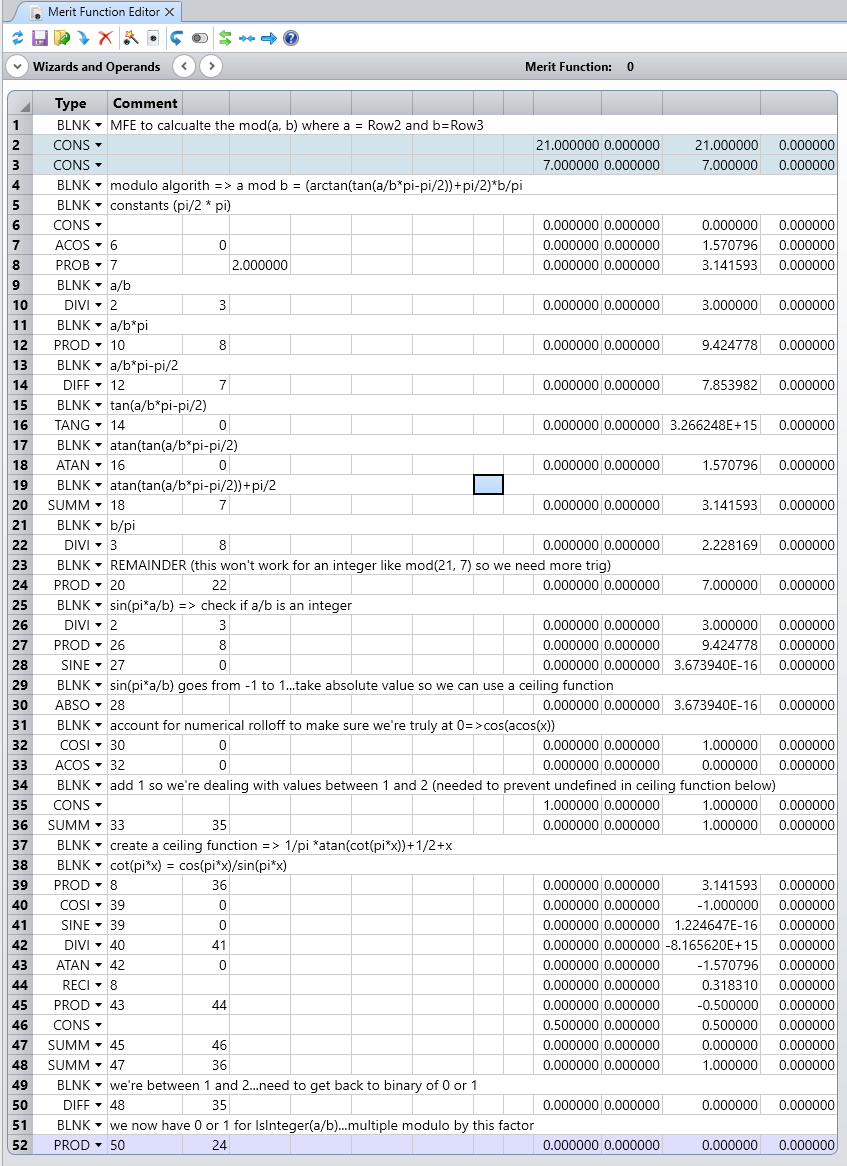
int denominator = (int)TheApplication.OperandArgument2;
...
double numerator_value = TheSystem.MFE.GetOperandAt(numerator).Value;
double denominator_value = TheSystem.MFE.GetOperandAt(denominator).Value;
operandResults[0] = numerator_value % denominator_value;To install, download the ZIP file, extract it, and move UDOC12.exe to your
Documents/Zemax/ZOS-API/Operands
folder. Then, in the MFE you can do:
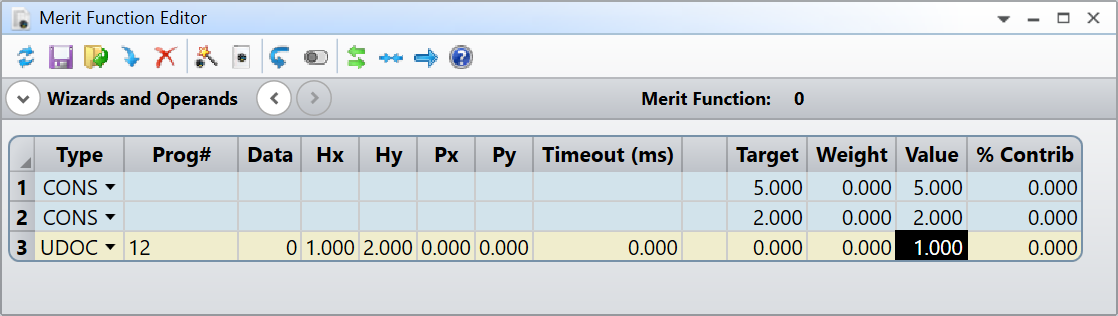
The rest of the division of 5.00 by 2.00 is 1.00.
In case you are wondering why I made this. I needed to have a linear polarization without caring about the orientation. I noticed that using CODA with data=110 (phase difference), some linear polarization angles were not achievable somehow and if I tried known configurations that would produce a linear polarization at those unachievable angles, CODA with data=110 would report 2pi. So, to make my original Merit function work, I’m just making sure that CODA with data=110 modulo 2pi is always zero :)
Hope this helps. Take care,
David