To compute the ABCD matrix, OpticStudio traces rays over a very small region centered upon the reference field position. Usually, this is the center of the field of view. OpticStudio allows selection of which field position to use for reference.By default, OpticStudio sets the corner of the field grid in object space to be at the maximum radial field distance. Because object height is linear with the tangent of the field angle, the full width of the field when angles are used to define the field is given by
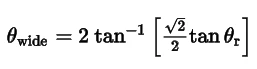
Where θr is the maximum radial field angle at the corner of the field.
The ray coordinates in image space for the very small field of view are used to determine the ABCD matrix components. The use of an ABCD matrix allows for coordinate rotations. If the image surface is rotated, such that a y object coordinate images to both an x and a y image coordinate, the ABCD matrix will automatically account for the rotation. The grid distortion plot shows the linear grid, and then marks the actual chief ray intercept for a ray with the same linear field coordinates with an "X" for each point on the grid.
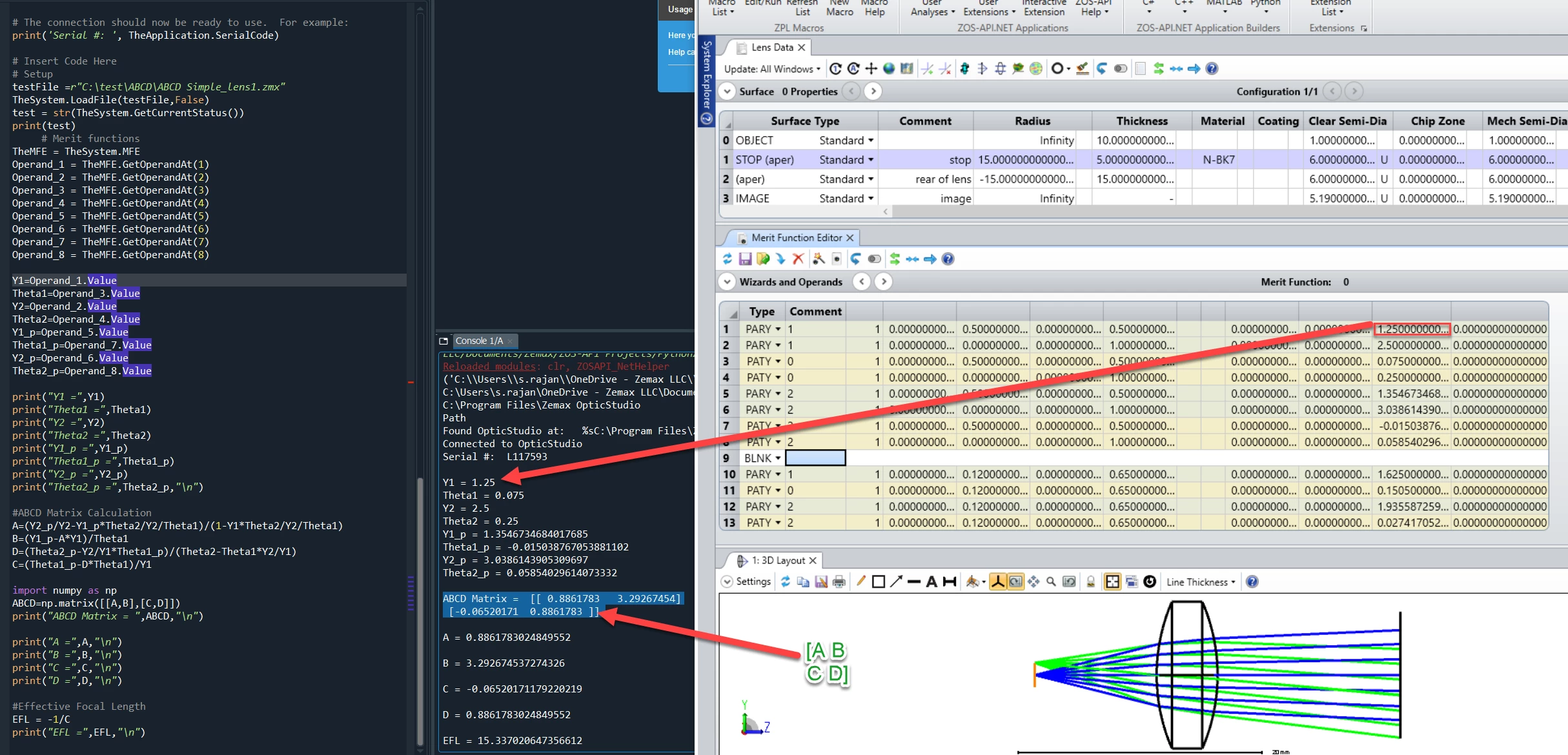
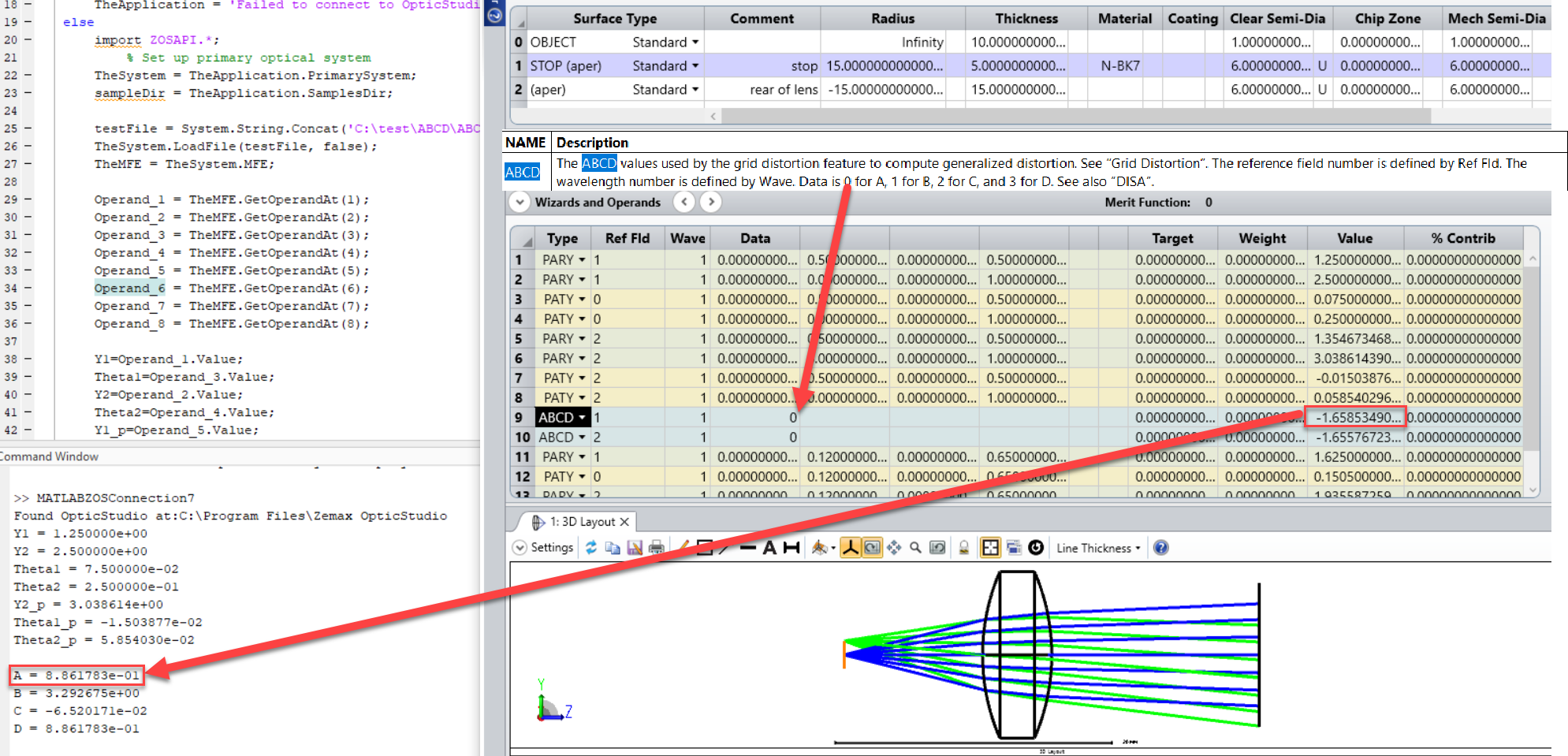
In OpticStudio, we can calculate the Ray transfer (ABCD) matrix using ZOS API(MATLAB and Python Interactive Extension). My colleague has an idea of doing using operands .We can calculate ray transfer matrix element by knowing Height of incidenct ray,Height of refracted ray ,angle of incidence and angle of refraction .As we have PARY or PAXY operands for showing the height of Ray in X or Y -coordinate respectively and PATY shows tangent of the angle the paraxial ray makes in the Y-Z plane after refraction .As shown in image1 below.
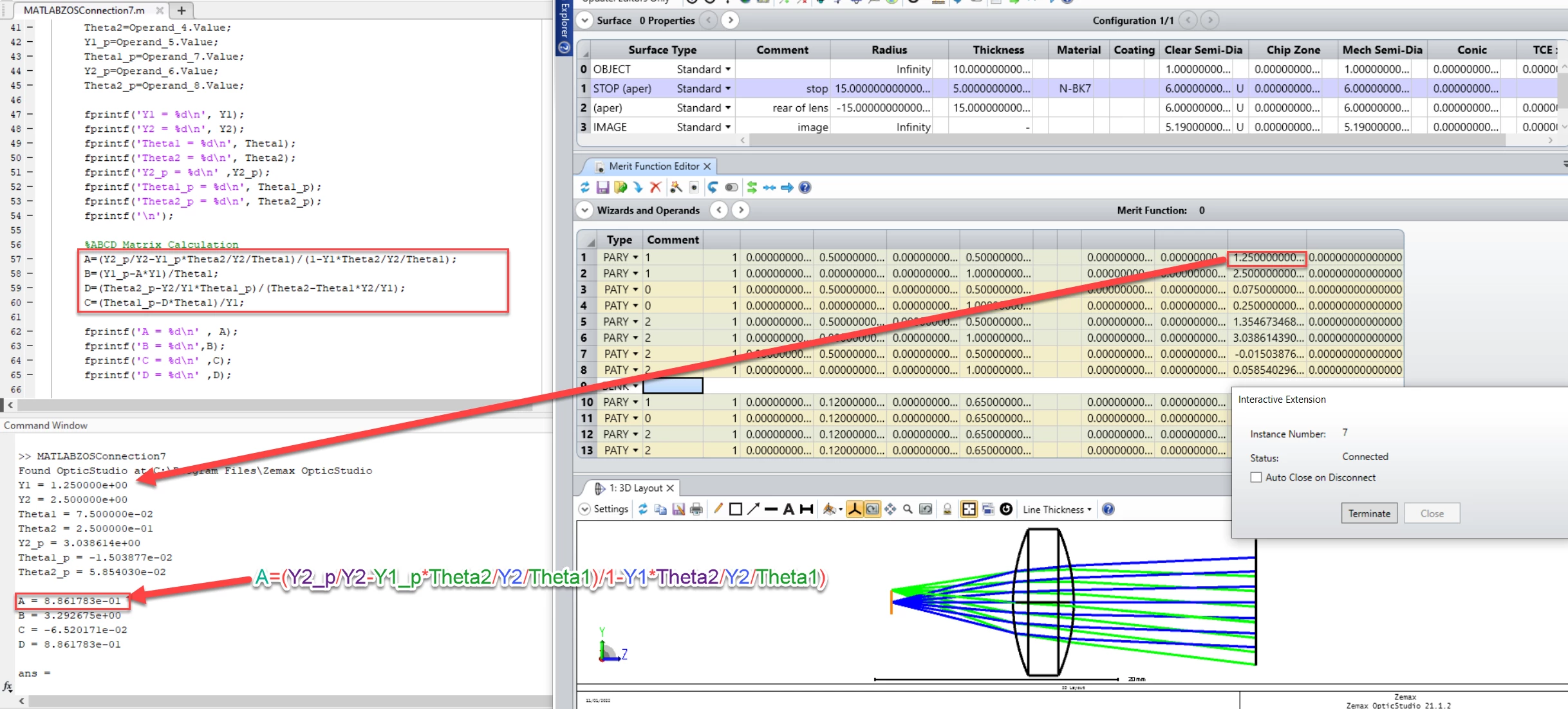
We can export angle of incidence and angle of refraction using PATY Operand and Height of incidenct ray and Height of refracted ray using PARY inYZ Plane to a variable in Matlab .Using these values to calculate A,B,C and D Values for Ray Transfer Matrix . In this Image 2, we can see the ABCD Matrix value in Matlab output console uisng MATLAB-API Interactive extension.
Similar in Python we can obtain value for ABCD Matrix shown in Image 3.
. Aberration theory predicts a ray’s location incorrectly, and for some reason lost to history we consider the real ray location to be ‘aberrated’ with respect to the theory. ABCDs should only ever work with real ray data: measured (real) position and angle on the left and measured position and angle of the right. What’s lost is the optical path length added or subtracted, which is why ABCD surfaces are not useful for imaging purposes
