簡介
在本知識庫中的 “如何進行序列模式公差分析” 這篇文章中，我們簡單說明了RSS的計算方式如下：

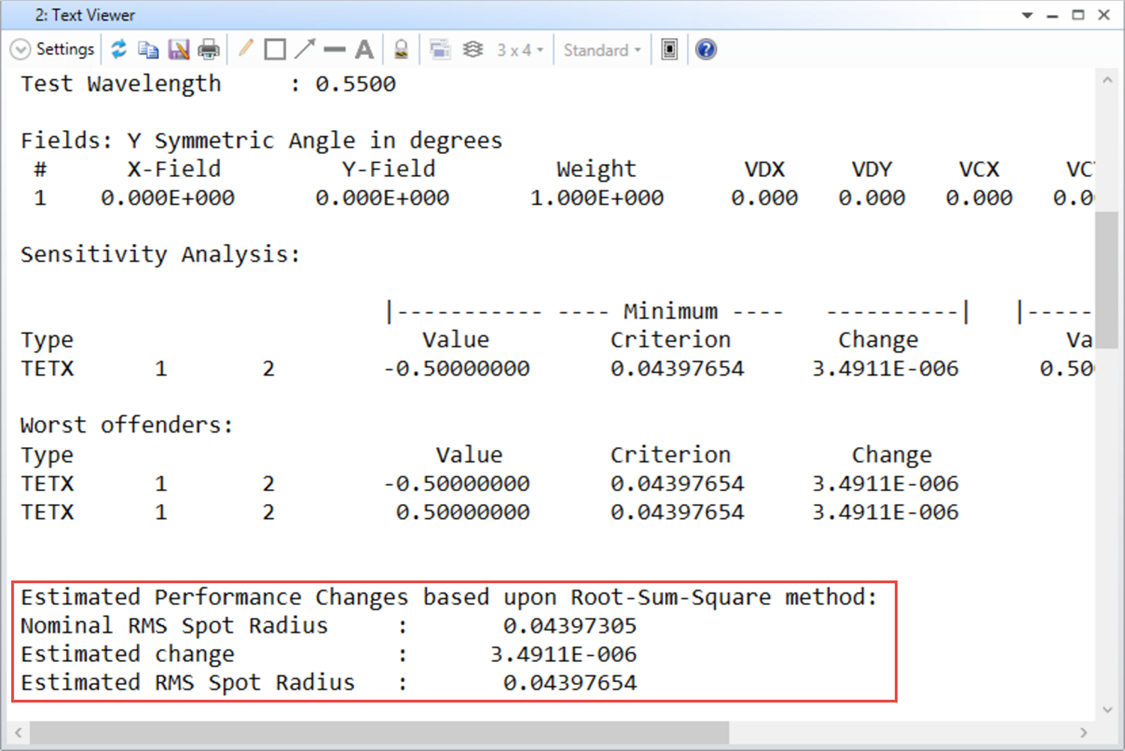
在所有公差單獨計算之後，OpticStudio可以計算各種不同的統計資料，其中最重要的就是 "Estimated Change" 以及 “Estimated Performance” (本範例中為Estimated RMS Wavefront)。Zemax使用RSS (Root Sum Square) 方法來計算品質的Estimated Change。對於每一個公差操作數，相對於原始設計的評價標準改變量之計算方法是最大與最小公差的評價標準改變各自平方，然後再取平均。最大與最小值之所以取平均是因為它們不可能同時發生，如果相加的話會導致過分悲觀的預測。

我們將用公差統計中的堆疊問題 (Stack Up) 說明 RSS 的計算。

堆疊問題
問題的描述是這樣的：
想像我們有5個木板要疊在一起，並需要估計疊在一起的總厚度。已知每一片木板的厚度都有些許不同 (現實世界總是會有誤差！)，每片木板的厚度大約在25 mm加減0.1 mm的範圍內隨機分布。假設這些木板的厚度機率是常態分布，中心是25 mm，機率最大，25.1 mm跟24.9 mm的機率則是e^-2，剛好會是距離中心兩倍標準差 (sigma) 的位置，畫出來如下圖。
 

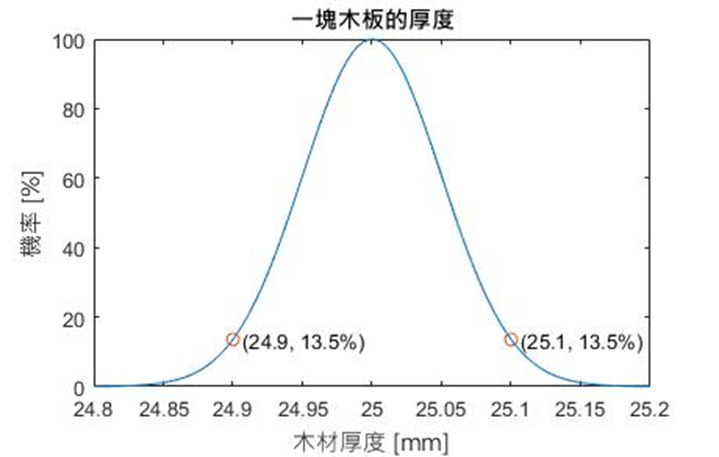
好，所以現在問題是，如果我們疊了5塊木板以後，厚度的機率分布會變成怎樣？
 

答案是125 mm加減0.224  mm。並且也會是常態分佈。以125作為中心，125.224與124.776的位置發生機率恰好是e^-2。

換句話說，整個系統的總厚度：
1. 也是常態分佈。
2. 常態分佈中心剛好是每塊木板的各自機率分佈的中心的總合：5+5+5+5+5=125。
3. 整個系統常態分佈機率為e^-2的地方，會是每塊木板各自常態分佈為e^-2時的偏差值 (deviation) 各自平方後、再加總、再開根號，也就是所謂的Root Sum Square (RSS)，你可以在Excel中輸入這右邊這串計算來驗證：sqrt(0.1^2+0.1^2+0.1^2+0.1^2+0.1^2)。答案正是0.224。

詳細的證明可以參考Wiki的說明：https://en.wikipedia.org/wiki/Sum_of_normally_distributed_random_variables

解讀與假設
看到這裡就能理解，RSS Deviation (偏差) 代表的是整個系統最終落在這個範圍內的機率是95.4%。以前面的例子來說，最終五片木板的厚度落在正負0.224範圍內的機率是95.4%。
 

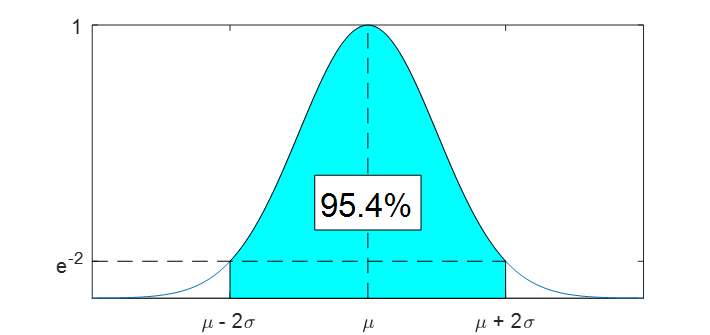
必須注意的是，這樣的估計方式有兩個重要假設：
1. 每個變數的影響都是常態分佈。
>> 例如前面例子中每個木板的厚度都是常態分佈，其標準差是0.05。 (注意前面說的正負0.1是標準差的兩倍，也就是2 sigma)
2. 變數之間的關係是互相獨立的。
>> 每一片木板的厚度變化對整體厚度的影響不會受到其他木板的影響。木板a偏差+0.03，不論木板b偏差是-0.07還是0.01或其他數字，木板a對整體系統的影響就是+0.03，不會受到其他變數大小影響。

回到光學系統公差分析
總結上面，回到我們的OpticStudio公差分析。
在看Estimated Change時，我們應該說，如果各個公差都符合常態分佈與變數互相獨立之假設，則代表統計上最終會有95.4%的系統，他們距離Nomial (標稱值，或說原始設計值) Criterion偏差都小於Estimated Change。
而對於Estimated Performance (可能是RMS Spot Size或其他你設定的值)，我們則可以說，95.4%以上的系統，他們的效能都會比這個數值還要 “好”。這就是為什麼我們說蒙地卡羅分析時，很少系統會比這個數值還差，並且可以把RSS Performance當作最差系統的原因。

範例驗證
讓我們打開一個內建範例來驗證：\Zemax\Samples\Sequential\Objectives\Cooke 40 degree field.zmx。
 

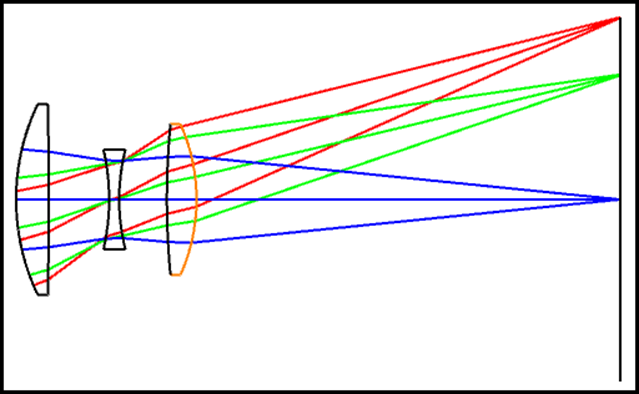
在公差編輯器中輸入簡單的6個公差，我們只分析第一片與第二片鏡片的傾斜、離心與鏡片厚度。並設有一個後焦距補償COMP，可以補償TTHI造成的離焦。
 

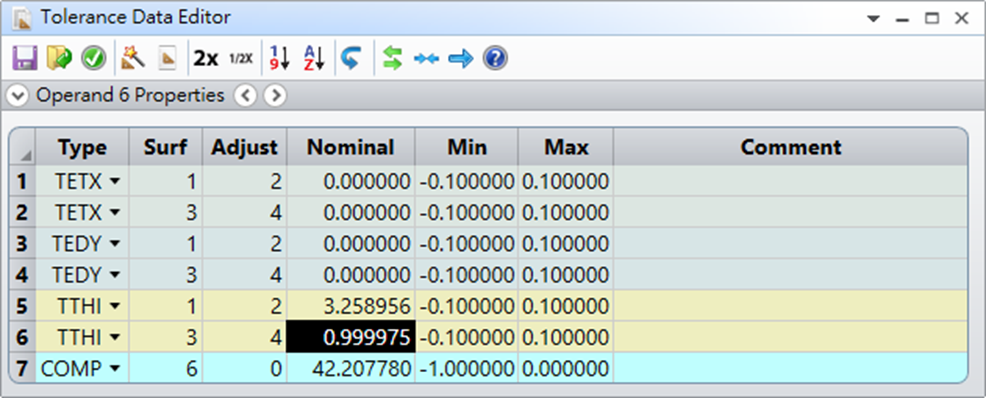
公差分析設定如下
 

執行完畢後，可以看到Estimated Performance的值如下：
 

而對比一下就可以發現大約是落在Monte Carlo的分析中的90%到98%之間。
 

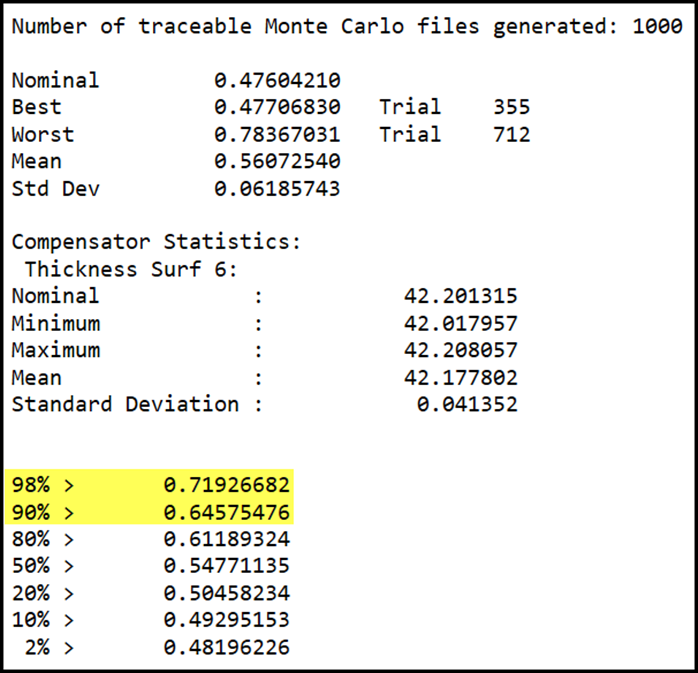
須注意由於在系統中，不像疊木塊這麼單純，一些公差，例如傾斜與離心，不是完全獨立。因此有時候RSS分析的結果會比蒙地卡羅預測的還要更差 (尤其公差非常寬鬆時)。