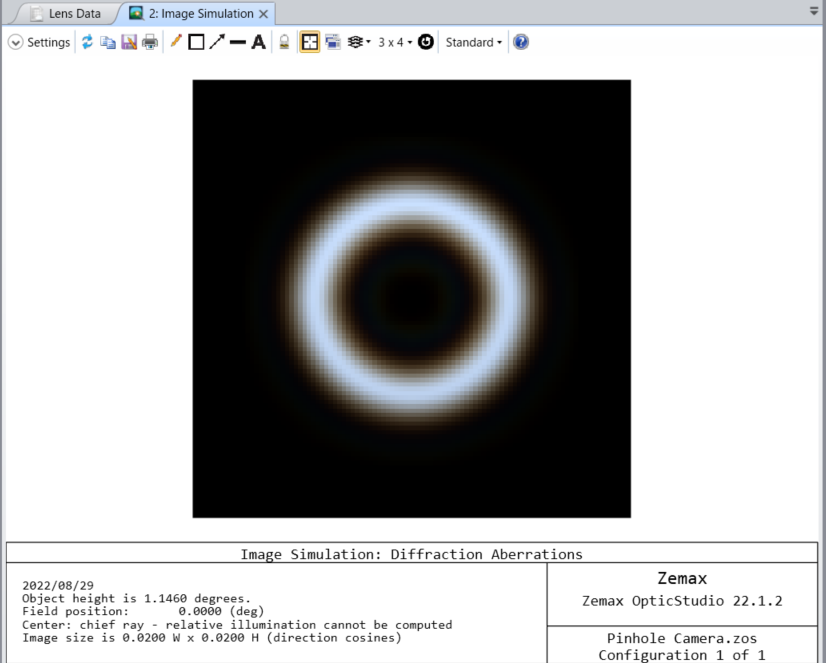
以下のポストで作成したピンホールカメラを使って、2012年5月21日の金環日食を観測したときのシミュレーション事例を紹介します。
ピンホールカメラで観測した金環日食のシミュレーション
Best answer by Takashi Matsumoto
まずは当日の太陽と月のデータを確認します。
国立天文台のサイトの「日食各地予報」の「指定地点の予報」に掲載されている通りで、視半径は太陽が948秒、月が891秒で、東京では食の最大で両者の中心距離が2秒になります。
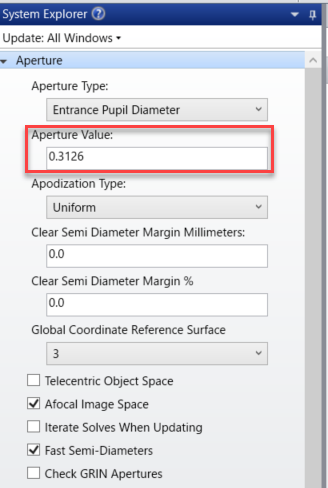
この記事では ピンホールカメラの解析 | Zemax Community で解析した、入射瞳径を0.7とする、ピンホールカメラの光学系を用います。詳しくはこちらのポストを参考にしてください。
今回は上記のファイルに2面まず追加します。
第2面の厚みを206,265mm として、絞り面の前の位置に物面を設定します。
この厚みの意味は、
206265×Tan(1秒)=1
ですので、物面の1mm が視角の1秒 に対応して便利だからです。
ピンホールカメラの解析事例の場合と異なり、今回は物体面までの距離が有限となりますので、絞り面には上記距離と等しい焦点距離を持つ近軸レンズを設置して、物面から出た光線が平行光として像面に入射するようにしています。
絞り面から像面までの距離は任意で、シミュレーション結果に影響を与えませんが、今回の場合はピンホールカメラの解析で用いた300mmを使用します。

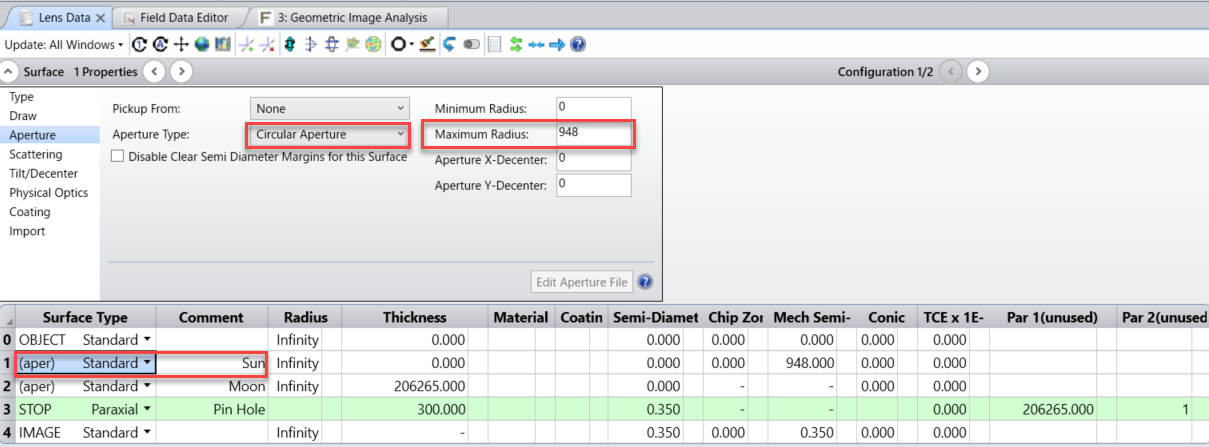
第1面の設定で以下の様に半径 948mm の円形アパチャーを設定し、太陽を表現します。
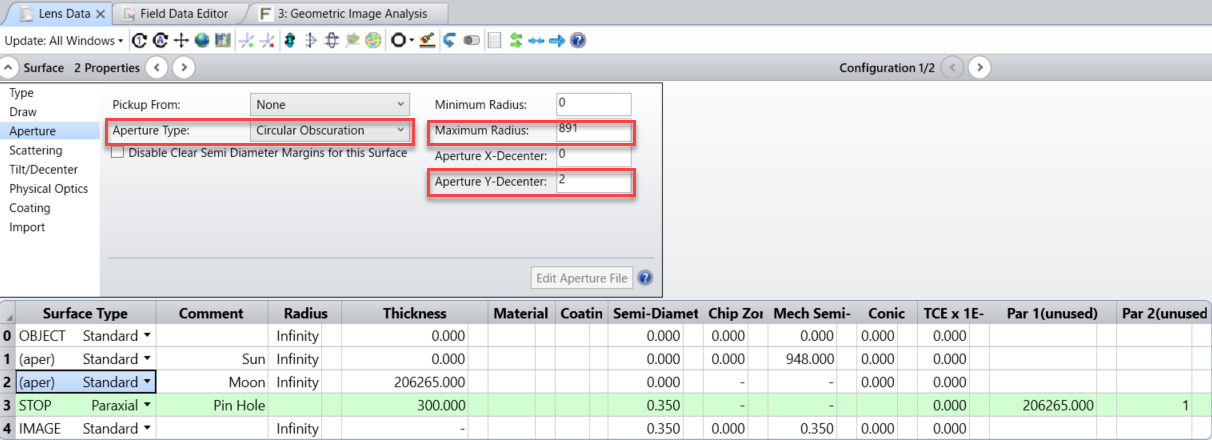
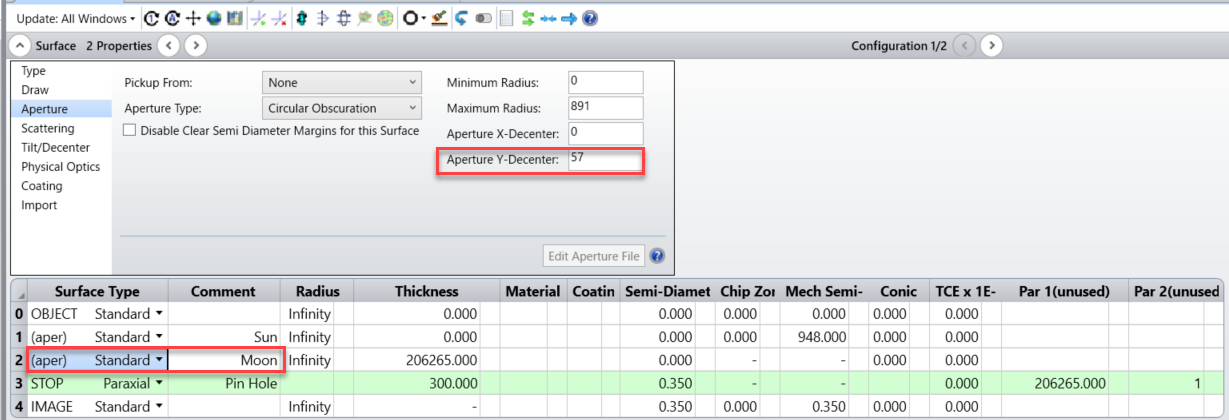
第2面は以下の様に半径891mmの円形遮光を2mmディセンタさせて設定して月と、食の最大を表現します。
ここで設定タブの視野データエディタを開き、「視野データ」のタイプを「物体高」を選択します。
これはこの後の解析に必要な設定です。
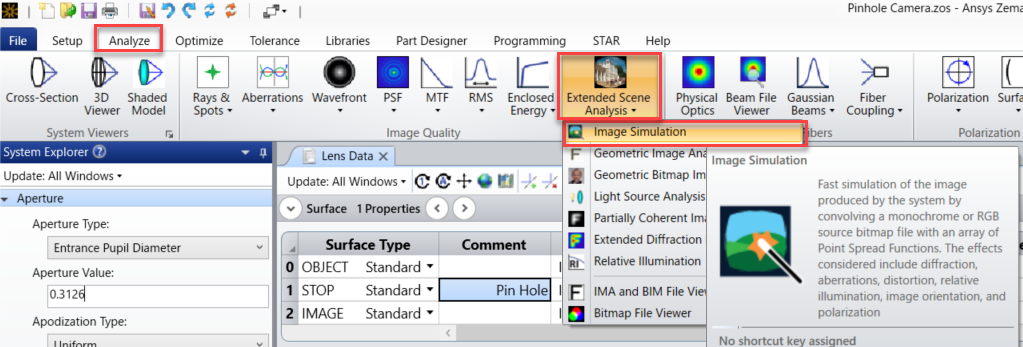
次に解析タブの拡張光源解析アイコンから 幾何光学的像解析
をクリックします。
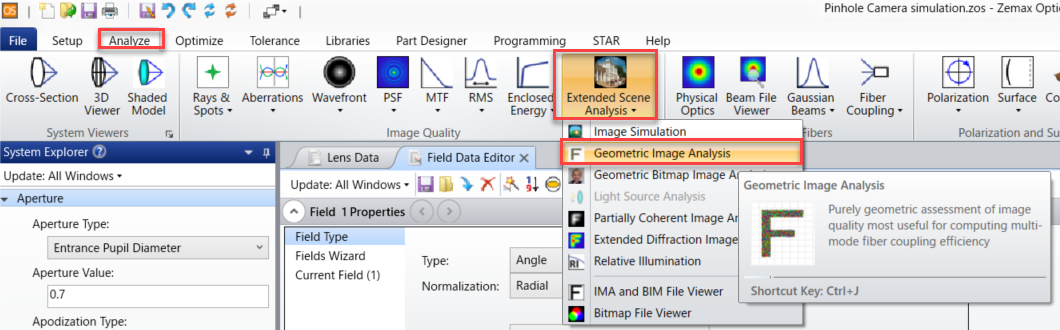
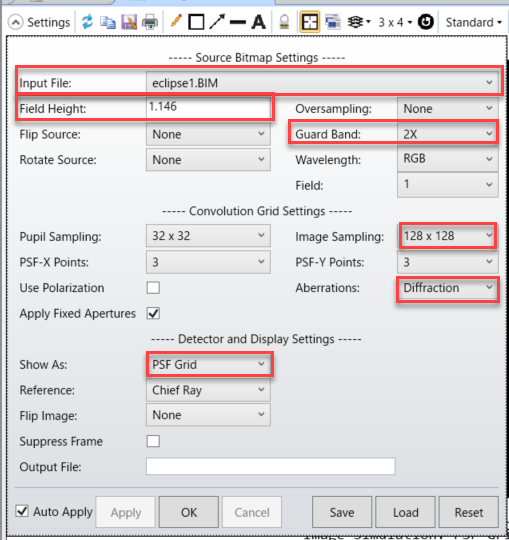
幾何光学的像解析の設定を以下のようにします。
「視野サイズ」は、物体面に適応するIMAまたはBIMファイルのY方向の全幅を表します。
この際の単位は視野の単位を使用するため、物体高を設定したため「距離」(ミリメートル)となります。従って直径1896mmの面光源を定義するという意味になります。
一方、「画像サイズ」は像面での解析範囲を表しており、ディテクタの大きさのY方向の全幅を表します。アフォーカルモードで使用する場合は、アフォーカルモード単位が適応されるため、画像のピクセルの表す単位は「ラジアン」となります。
ファイルとして "SQUARE.IMA" を指定すると、中央の抜けた口の字状の光源が指定されますので、今回はこれのファイルを使用します。
最後に、一番下のBIMファイル欄に
eclipse1.BIM
と入力して、この名でBIMファイルが作成されるようにします。
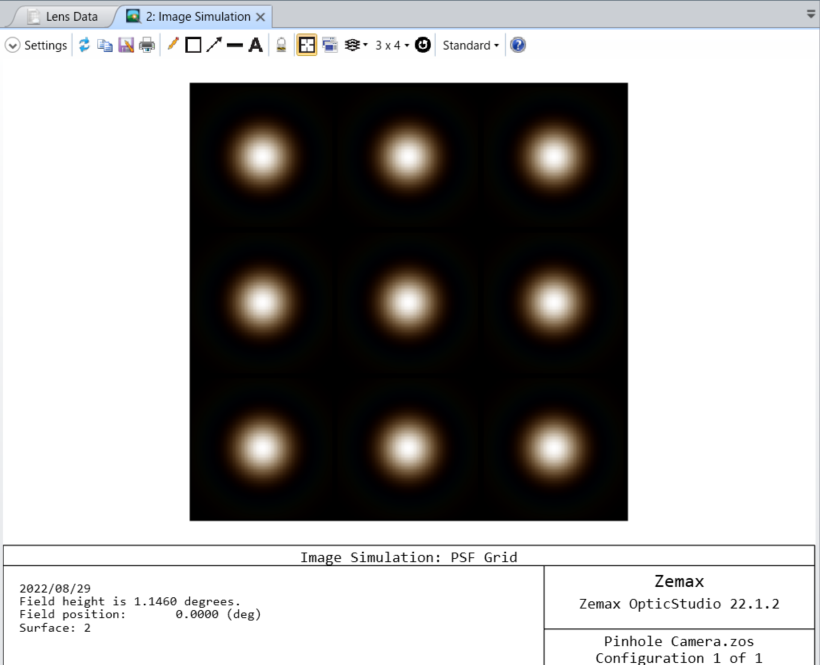
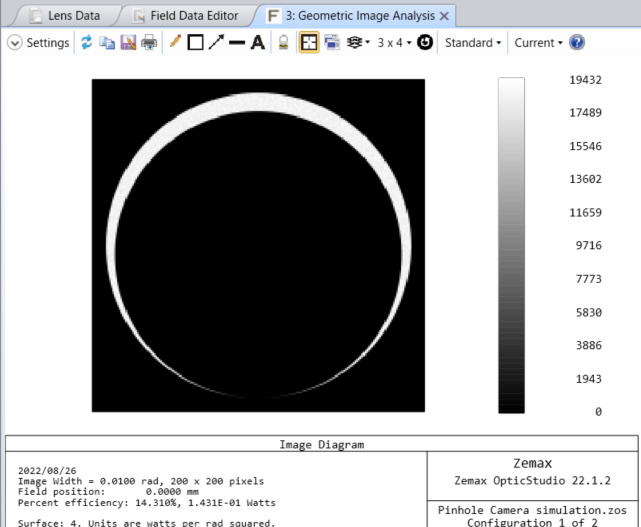
結果は以下の様になります。
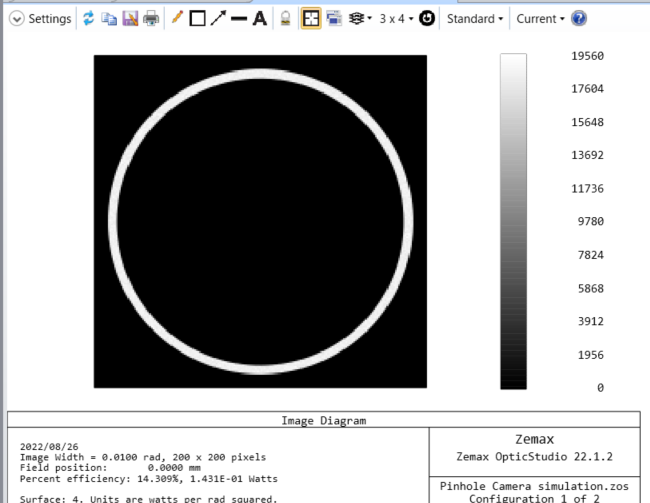
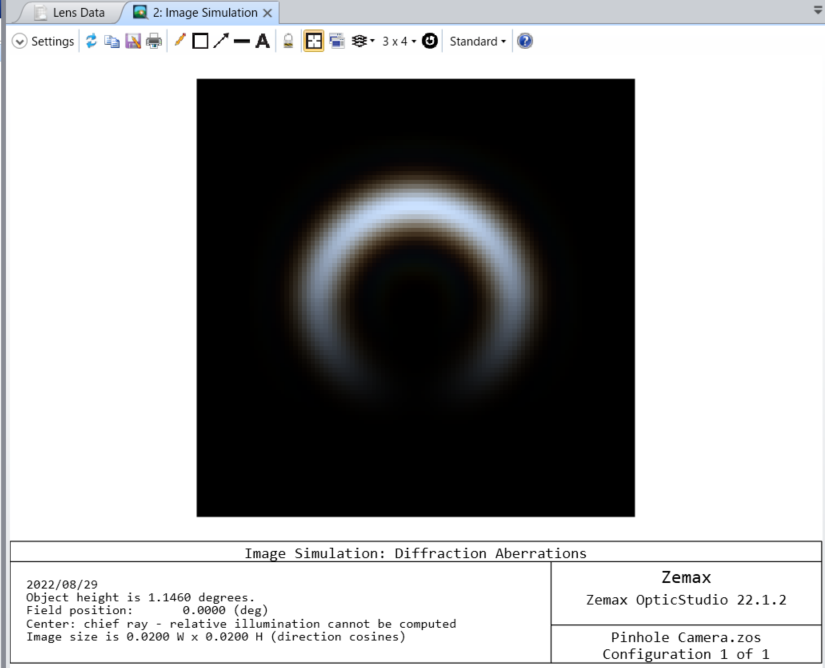
上図は食が最大になったときのシミュレーションでしたが、下図のように第2面のディセンタを 57 とすると、月と太陽の縁が接したときのシミュレーションが可能です。
結果は以下の様になります。
本例のZARファイルも添付しましたので、参考にしていただければと存じます。
Enter your E-mail address. We'll send you an e-mail with instructions to reset your password.