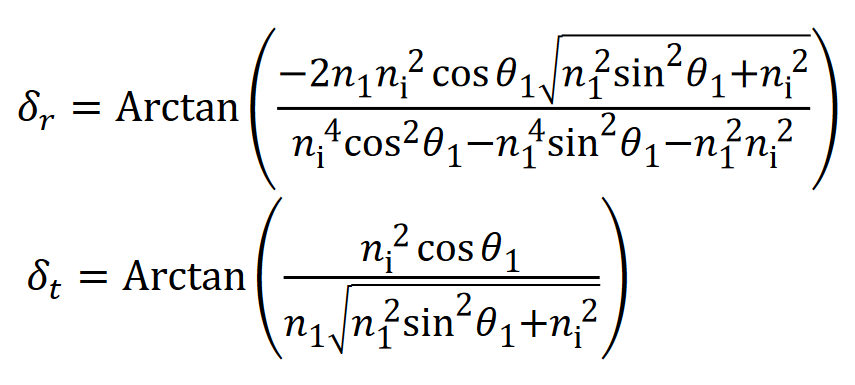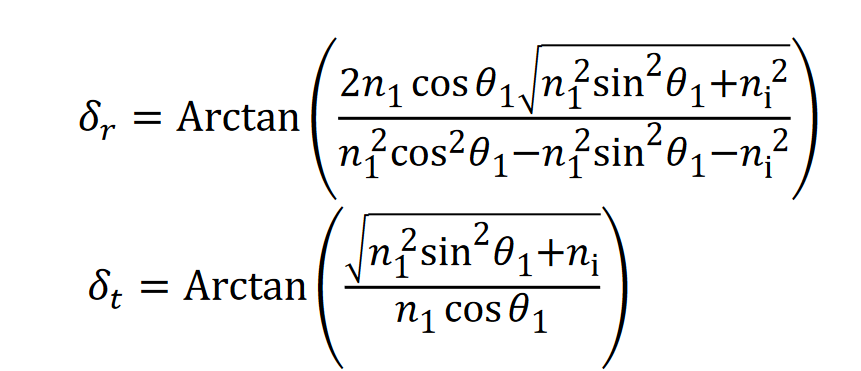Light reflected by a metal at non-normal incidence will generally have its ellipticity changed. Our case is a 45 degree angle, so it is non-normal.

https://en.wikipedia.org/wiki/Circular_polarization#Via_reflection
When we set the surface property to “MIRROR”, it is set as some metal surface, and retains the properties of that metal.
For an ideal reflecting surface, I can set the coating of the MIRROR surface to “I.0”, which is a non-absorbing perfect reflecting surface. I get the result your intuition tells you, that the reflected polarization is not elliptical. This ideal reflection does not have any metallic or physical properties.
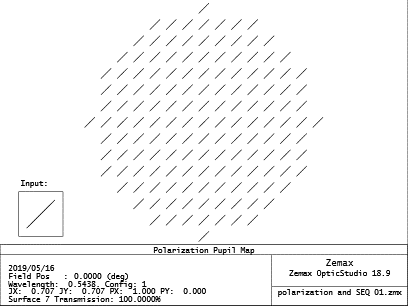
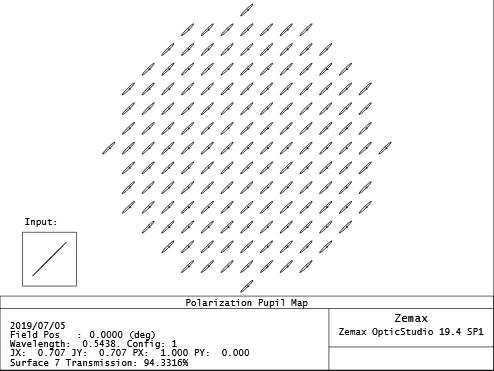
If I set the coating to “GOLD”, I get the following, much worse.
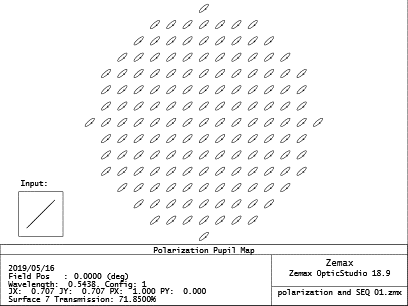
The physics behind it is a little involved, but essentially, the S and P waves for the polarization are different with respect to the incident angle for most metals.
Below for the S-wave,
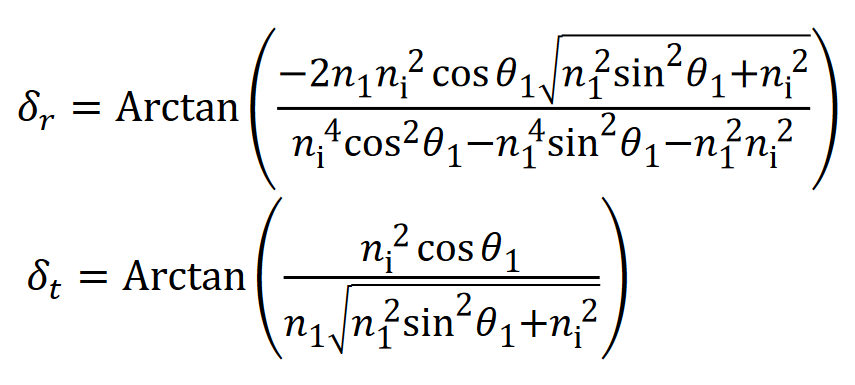
Below for the P-wave.
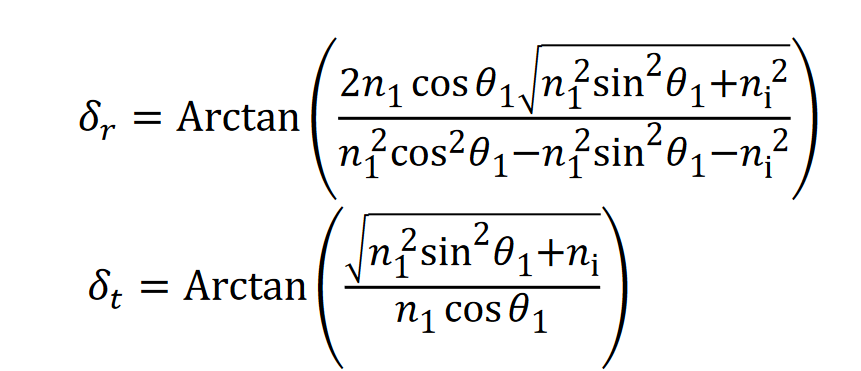
If we plot this out for a random metal, it looks something like this:
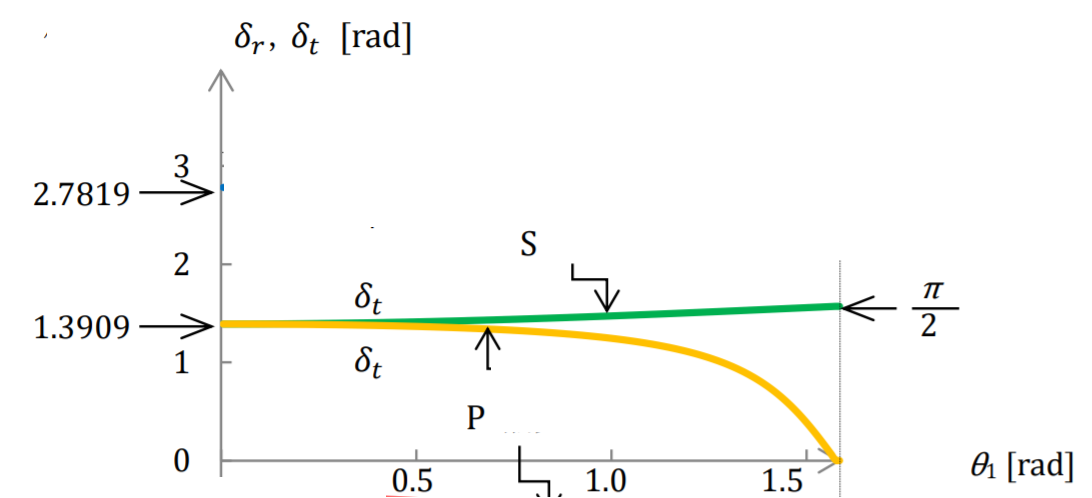
The incident angle is Theta_1, so you can see that the two reflections are different for non-zero indicent angles. For 45 degrees, we are talking roughly where the arrow for “P” points, so the difference between S and P are small in this case. 45-degrees is usually the tipping point that this happens, it's usually much worse at larger angles. We can also see that the reflection for Theta_1 = 0, or normal incidence, is Pi as expected.
I hope this helps.