I have a very simple model that I want to completely understand, but seem to be having an issue with the sign of the electric field of the source ray.
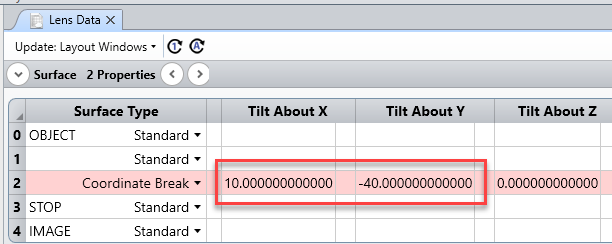
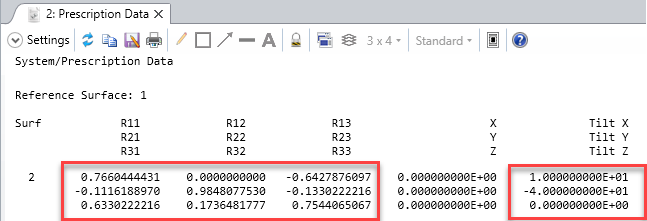
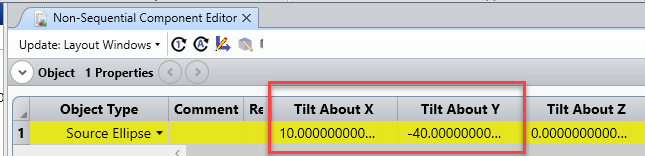
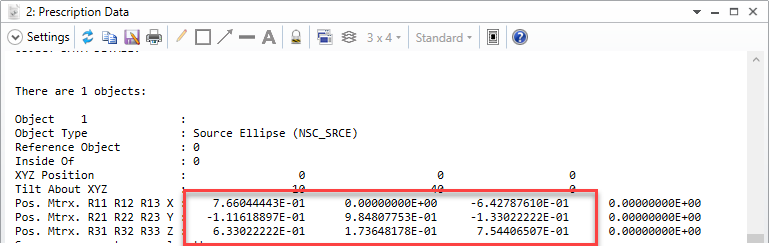
Suppose I launch a single ray, with a YTilt of 10 deg and polarization of Jx=Jy=1 using the Z-axis as my polarization reference. Then my initial K vector will be [x0.139173, y0, z0.990268]. According to the knowledgebase article (https://my.zemax.com/en-US/Knowledge-Base/kb-article/?ka=KA-01336#TypesPolarizationDependentMedia) , my S and P vectors are given by
S = k x Z = [x0, y(-0.139173), z0]
P = k x S = [x0.137818, y0, z(-0.019379)]
Now I would like to know precisely how S and P are converted to my initial electric field, E, which is not explicitly described by the aforementioned article. My thought is to normalize each polarization vector by their magnitude,
Sn = S / |S| = [x0, y(-1), z0]
Pn = P / |P| = [x0.990268, y0, z(-0.139173)],
then to scale these normalized quanities by the relative Jx/Jy values and intensity as follows:
Sn' = Sn*sqrt(Jx / (Jx + Jy) * IntensityPerRay) = [x0, y(-0.707106), z0]
Pn' = Pn*sqrt(Jy / (Jx + Jy) * IntensityPerRay) = [x0.700225, y0, z(-0.098410)],
with IntensityPerRay=1 if I only have a single analysis ray in my system and my source power=1. Finally we add these to get to the total electric field,
E = Sn' + Pn' = [x0.700225, y(-0.707106), z(-0.098410)],
from which we can recover the total intensity as Intensity = |E|^2 = 1. While this makes sense to me, the result in Zemax Optic Studio has a sign flip in the y-component of the initial electric field. It is
E_zos = [x0.700225, y0.707106, z(-0.098410)]
Can anyone please explain why the sign is flipped in ZOS, or if there is an error in my approach?! I have redone this simple math many times and cannot find any mistake. The ZOS file of a very simple model is attached. It is worth noting that if I change my Z definition to Z=[x0, y0, z(-1)], I do NOT recover the ZOS result.