I don’t understand some results generated by the Power Pupil Map analysis feature. Perhaps someone here in the forum can provide insight.
For a general lens system, consider the wavefront leaving the exit pupil. This wavefront is typically not spherical because of aberrations, or perhaps because the lens is a freeform optic. In either event, the min and max values of the local curvature at any point on the wavefront in the pupil determine the min and max focusing power associated with that pupil location. Equivalently, we can look at the max and min local focal lengths, which are just the reciprocals of the powers. The Power Pupil Map is a nice tool to help the user visual this effect. Several options are available for the form of the data. Also, a surface must be selected.
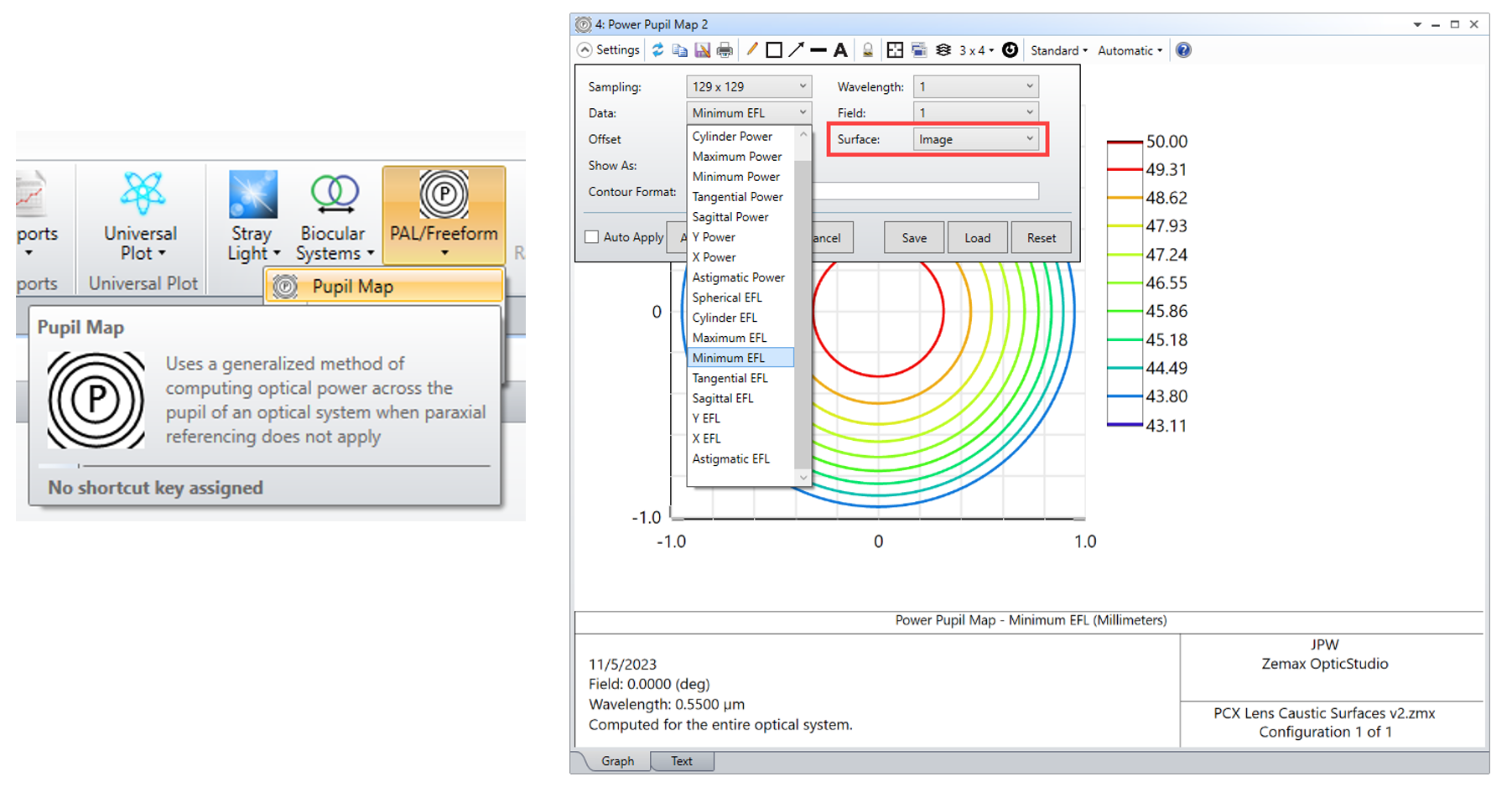
Consider a simple test case using a plano-convex lens that focuses an on-axis collimated beam. Spherical aberration causes the exit pupil wavefront to have local curvature that varies over the pupil.
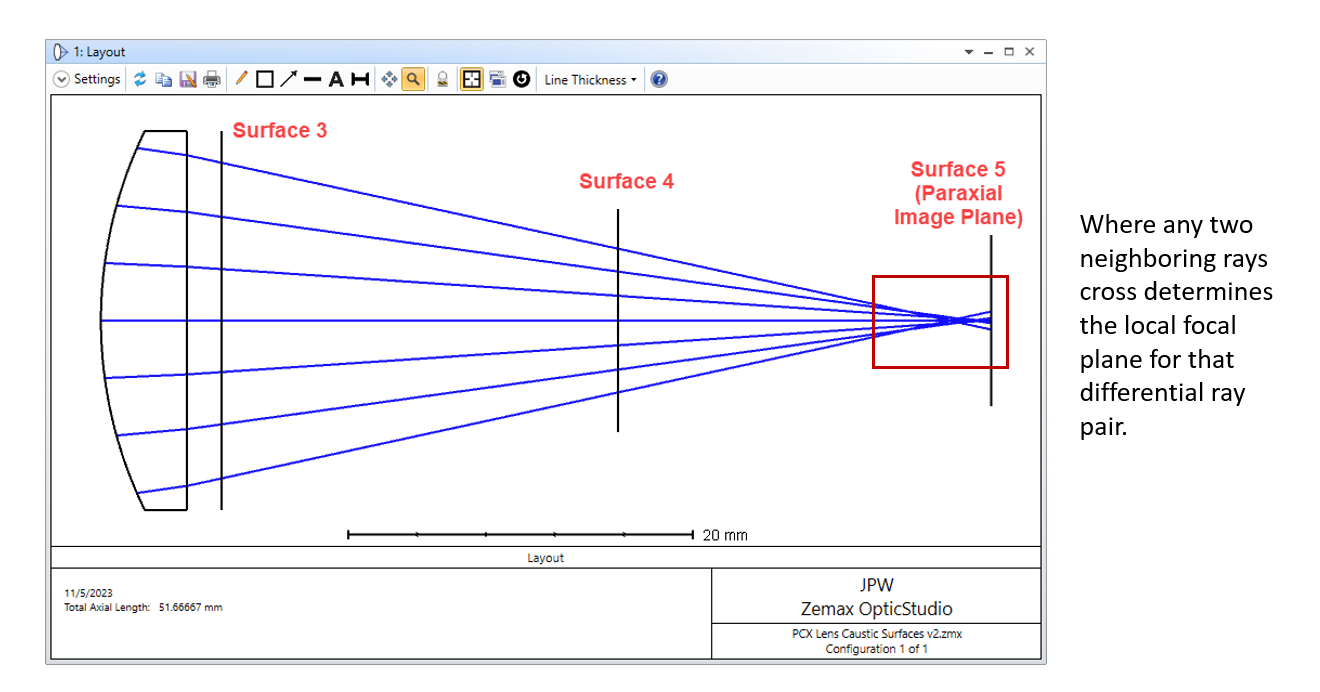
Presumably the effective focal length is found by looking for the z-location in image space at which two neighboring rays cross one another (or, if they don’t actually cross, where they reach minimum separation). Two neighboring rays in the center of the pupil will cross at the paraxial focal plane, whereas two neighboring rays at the edge of the pupil will cross closer to the lens. In general, for any point in the pupil there are two crossing locations that lead to max and min focal planes because the “neighboring ray” associated with any reference ray can be selected from a ring of rays in the pupil surrounding the reference ray. Let’s refer to the reference ray plus some neighboring ray as a differential ray pair.
For any differential ray pair, the corresponding local focusing power or local focal length can be found from the ray data at any location in image space. Presumably the “local effective focal length” is simply the z-distance between the local focal plane (i.e., the xy-plane where the rays cross, or come closest to crossing) and the image-space principal plane of the lens. However, when I look at the results for this test case, I find the effective focal length changes depending on which surface is selected (three options are shown above, all three are just planes in image space). Here are plots of the Max and Min effective focal length vs Py for the three surfaces:
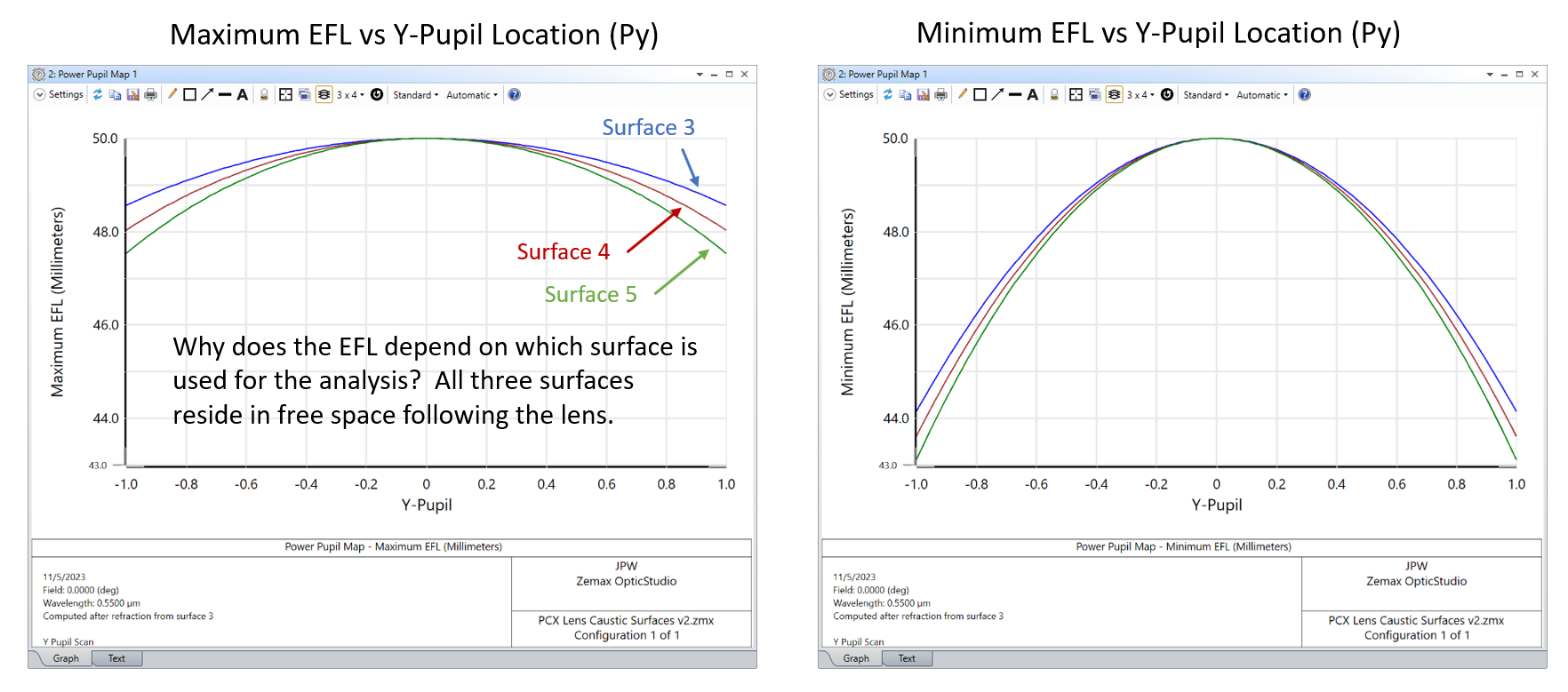
My question is: why are the results surface-dependent? Once the rays leave the lens, they are propagating in free space, and the location at which any differential ray pair crosses in image space should not depend on which surface is used to extract ray data for performing the calculation.
Upon digging a little deeper, it looks like selecting Surface 5 (which is the paraxial image plane) produces the correct results. I say this for two reasons. First, I’ve done my own numerical analysis of this test case and find results that agree with the Surface 5 selection. And second, only the min and max curves for Surface 5 lead to corresponding changes in focal distance that are related by a factor of three (which is known to be the case for spherical aberration -- see J. Sasian’s book, “Introduction to Aberrations in Optical Imaging Systems,” Eq. 9.5). If Surface 3 is selected, the max/min ratio of focal change is closer to 4.1, which seems incorrect.
So in this case it appears that picking the paraxial image surface is the way to go. However, the help documentation is at odds with this choice. It states:

In my test model, Surface 1 is actually the last surface that has power, but let’s assume the help documentation is referring to the last physical surface of the lens, which is Surface 2. This choice yields results that are close to those obtained when using Surface 3, but that’s to be expected since Surface 3 is only a few millimeters away from Surface 2. In any event, my main point here is that the help documentation would seemingly lead the user to select a surface that produces incorrect results.
Just curious if anybody has some thoughts on what is going on here? Maybe I’m missing something…
Thanks,
Jeff






