Hello Optic Studio friends,
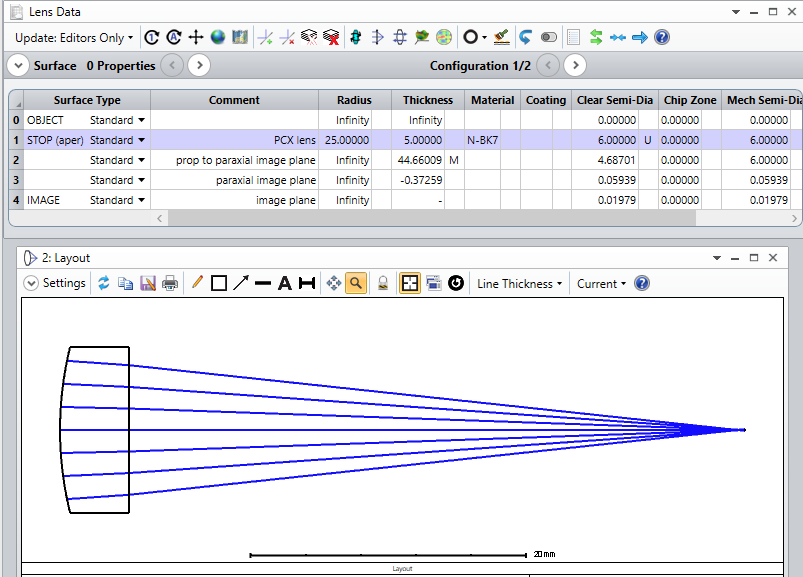
I have a question about the OPD calculation for an on-axis finite-finite imaging system.
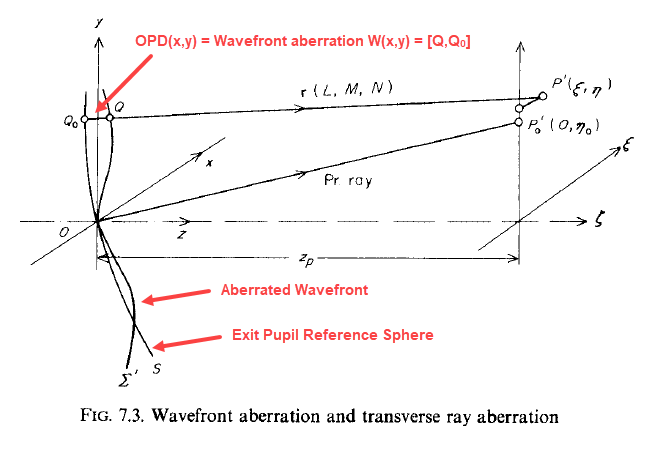
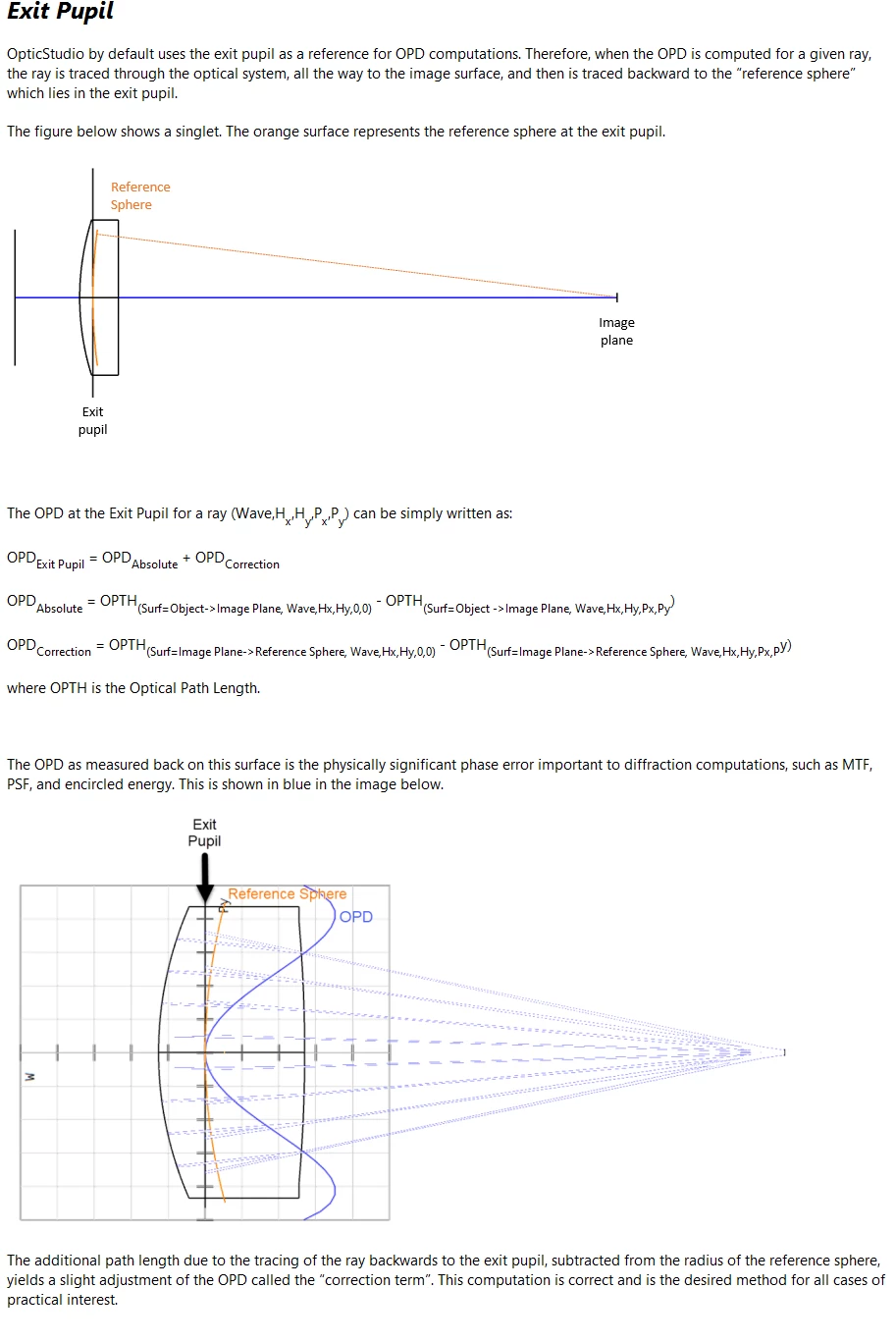
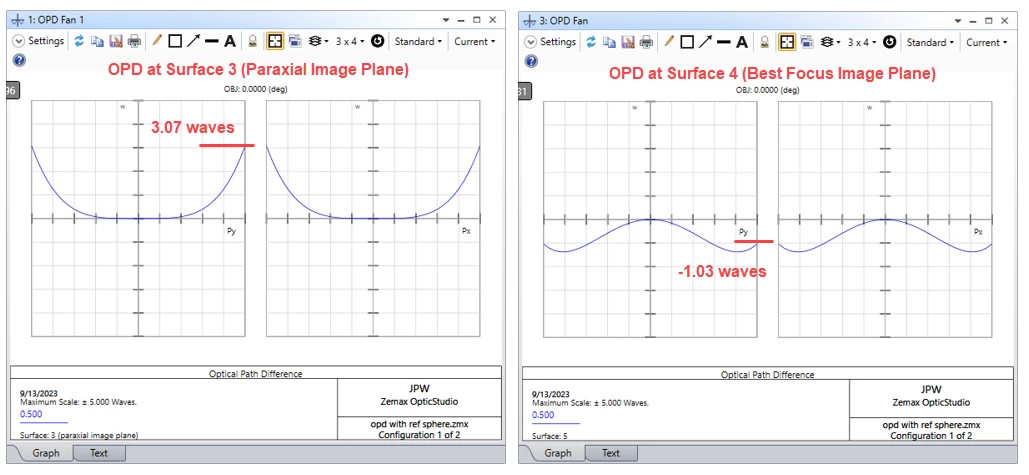
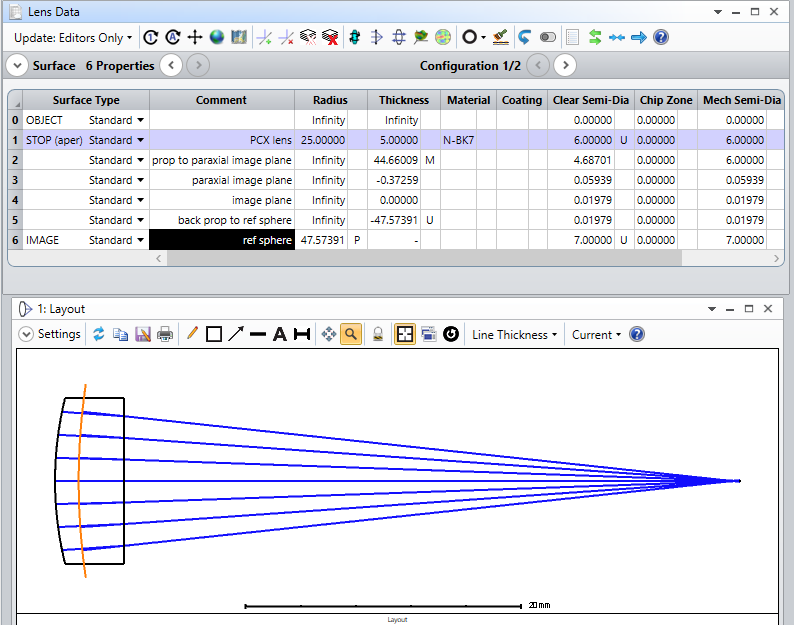
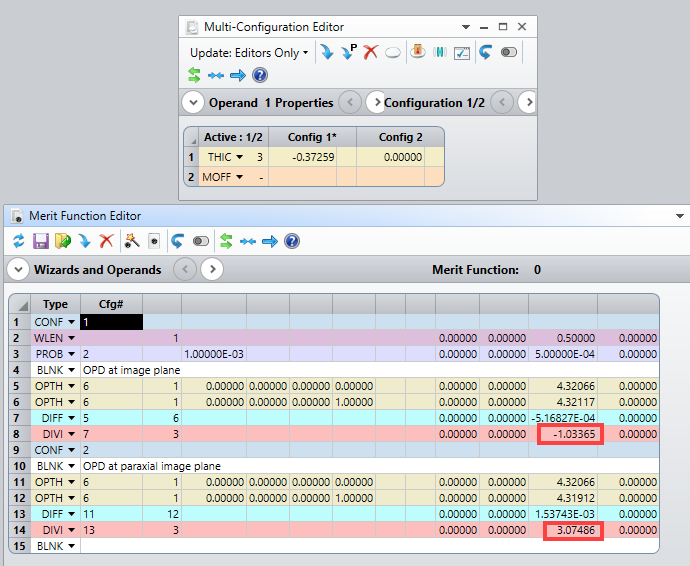
I have understand that OS calculates the OPD based on the reference sphere and that the OPD is calculated in the plane of the exit pupil.
How does Zemax calculate the exit pupil? Does it consider pupil aberration? Or does it assume that the pupil is just a plane? And is the pupil position the position you get when using paraxial ray trace equations (...what means that aberrations of the system are not considered)?
And I have another question regarding the reference sphere. Where is the center of the reference sphere located?
Is it located in the paraxial image plane?
Thanks and kind regards
Dirk
Question
OPD: Reference sphere and exit pupil
Enter your E-mail address. We'll send you an e-mail with instructions to reset your password.