There are two local optimization algorithms: Orthogonal Descent (OD) and Damped Least Squares (DLS).

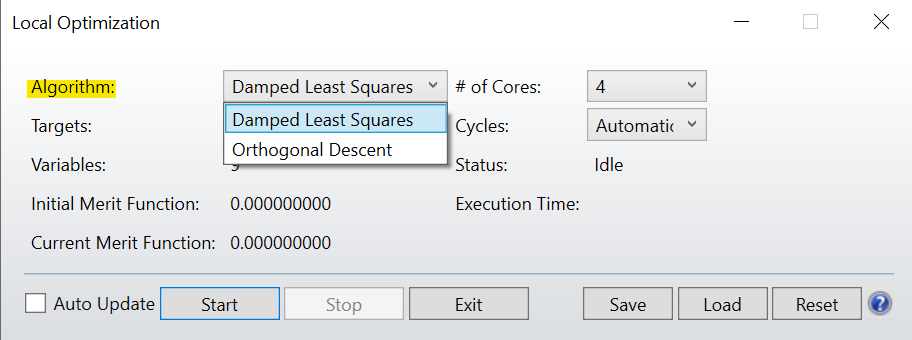
The OD algorithm uses an orthonormalization of the variables, then samples the solution space discretely in an attempt to decrease the merit function. DLS, on the other hand, actually calculates the numerical derivatives to determine what direction of change will result in a lower merit function. DLS is generally recommended, but for systems where the solution space is quite noisy, like illumination design or other non-sequential systems, the OD algorithm will likely outperform the DLS optimizer.

This applies anywhere these algorithms are used such as in Hammer optimization, Global optimization and tolerancing.

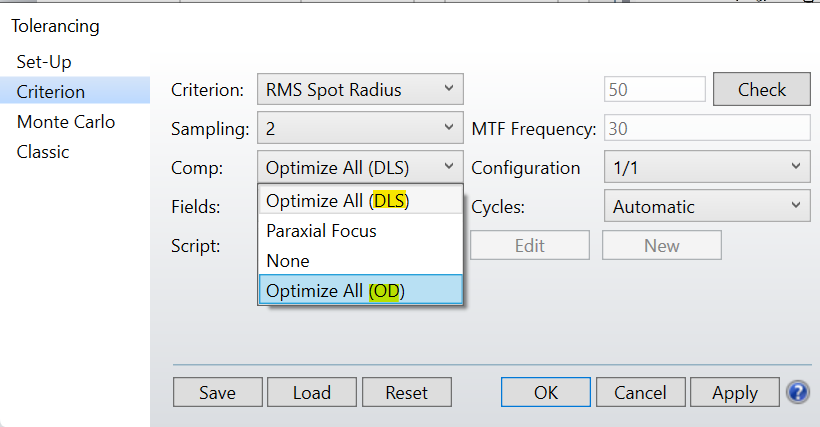
For example, to optimize the compensators in your system (and not just the paraxial back focus), you choose between “Optimize All (OD)” or “Optimize All (DLS)”. The first will just use the OD algorithm, while the second will use an initial cycle of OD followed by the DLS algorithm. OD is good for rough adjustments, and though I just said it is usually used for non-sequential systems, it is also useful in this application in tolerancing sequential systems.

Let me throw in my 10cents here. Everything Sarah says above is true, and I'd like to add some of the thoughts that led to the development of OD.

DLS optimization is ubiquitous in optical design codes because you typically have many-dimensional solution space. Each variable is a dimension of the solution, and a twenty dimensional space say (20 variables) is very common and in fact quite small. In addition, the merit function is reliably smooth and continuous, so a small change in a variable provides a small change in the merit function that can guide optimization. Last, we make no assumptions about the starting point's location relative to the final solution.

In non-sequential systems, there are several differences. Typically there are fewer variables in an NS system, by an order of magnitude or more. The merit function is often discontinuous AND noisy, so it is difficult to rely on a small change of a variable to provide a useful direction pointer. See this KB article for gory details.

Then, after it was developed, we realized that it was actually ideal for tolerancing too. In tolerancing there are typically only a few compensators. Compensators are just optimization variables with a fancy name. BUT, we can assume that the starting point is close to the local minimum, because we've simply perturbed a value by a small amount, and want to relax the compensators back to the minimum. That changes the problem significantly, as you're trying to find a local minimum that can be assumed to be close to the starting point. In this case, the OD algorithm is way better than the DLS optimizer.

The benefits of OD over DLS in tolerancing are:

• The OD algorithm is designed for fewer variables



• The OD algorithm is better at finding minima that are guaranteed to be close to the starting value

The noise benefit (OD is better in the presence of a noisy or discontinuous merit function) is not relevent at all, despite it being the main reason we wrote the OD optimizer.

There was a strong point of view (guess who) that the OD optimizer should be the only optimizer available in the tolerancer, as we couldn't find a case where the OD didn't outperform the DLS in this use case. However, not finding such a case does not mean that one does not exist, so we kept the DLS optimizer in the code, but called a single round of OD at the start in any case.

Remember also that when in tolerancing to not use the Automatic setting or a large number of cycles unless you have a specific, real need to do so. In tolerancing, we are perturbing away from a known good minimum, and so one round of optimization, two at most, is all you need to recover performance when you have a relatively small number of compensators (optimization variables) that are already close to the final solution.