Hello,
I have a very simple nonsequential model:
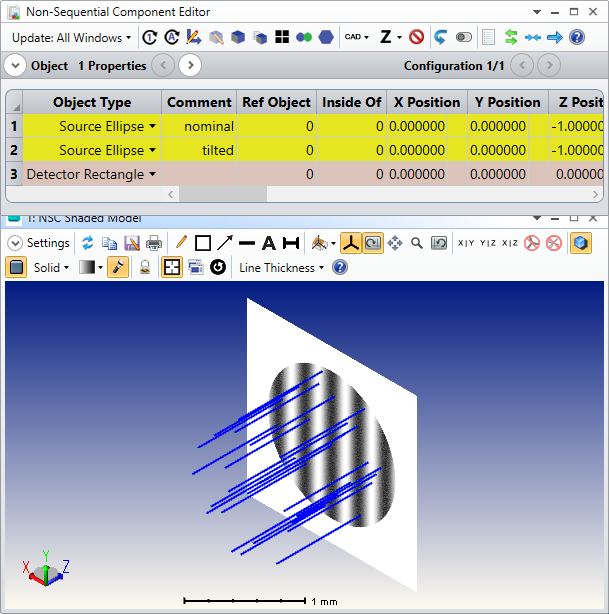
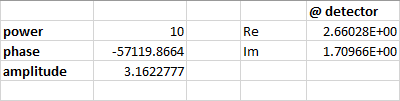
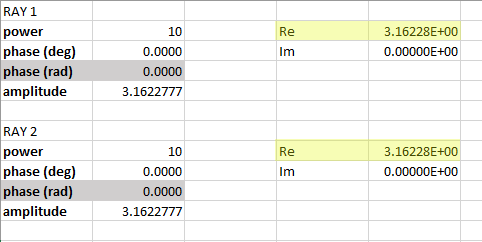
Source Point: power=10 W, coherence length=0, linear polarized: Jx=Jy=1, collimated light: cone angle=0
Detector rectangle: placed behind source, normal incidence, number of pixels=1, polarization=2 for measuring power of y-polarized light
Then I have a merit function:
NSDD for clearing the detector
NSTR for making the rey trace
NSDC for measuring nonsquential coherent data
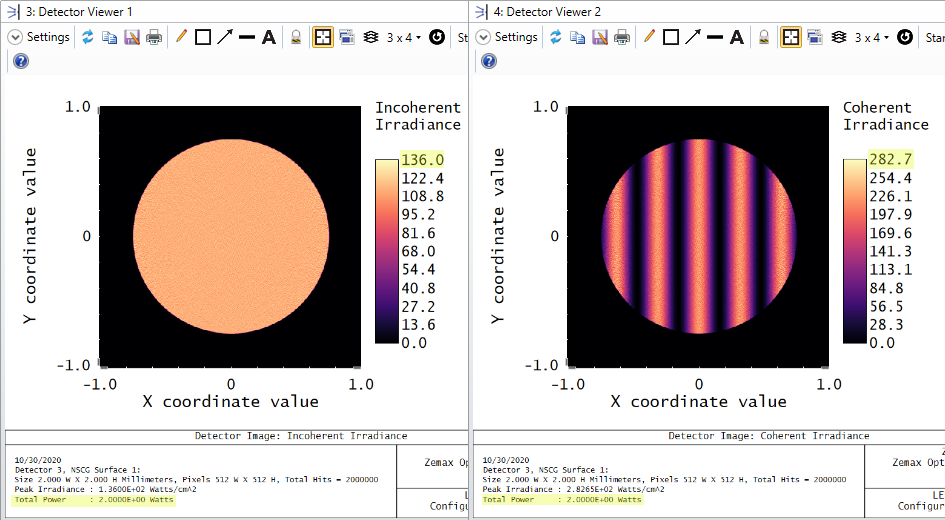
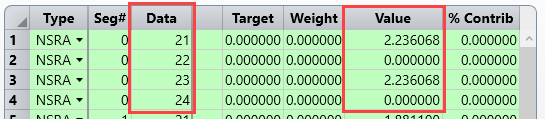
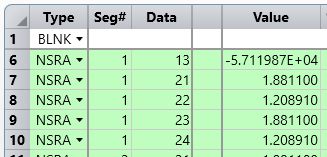
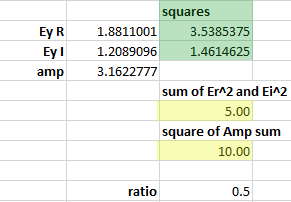
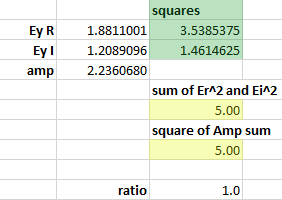
I was expecting to get Ey (y-component of the E-field vector), if I take Pix=0, Data=2 as parameters for NSDC.
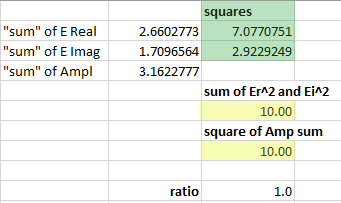
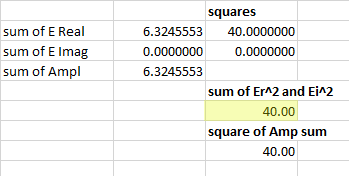
But I got 1,581 as result. From my understanding the result should be Sqrt(10)*cos(45°)=2,236. What's wrong here?
If I take Pix=0, Data=3 as parameters for NSDC I get 2,5 as result. Data=3 should calculate the power.
Because power is proportional to amplitude of E-Field vector and 1,581^2=2,5 this is consistent.
But according to Malus Law I was expecting to get 10W * (cos(45°))^2 = 5W.
I would be very happy if someone can help me clarifying this.
Thanks in advance and kind regards
Dirk








![{\displaystyle I(\mathbf {r} )=I_{1}(\mathbf {r} )+I_{2}(\mathbf {r} )+2{\sqrt {I_{1}(\mathbf {r} )I_{2}(\mathbf {r} )}}\cos[\varphi _{1}(\mathbf {r} )-\varphi _{2}(\mathbf {r} )].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f41265d6a2a8696fb6e681c5c64043ad1cfd644)