Question

Monte Carlo analysis: Spherical aberration with TIRR and comparison with ISO10110

  • 28 April 2023
  • 8 replies
  • 544 views
G

Dear Zemax Community,

 

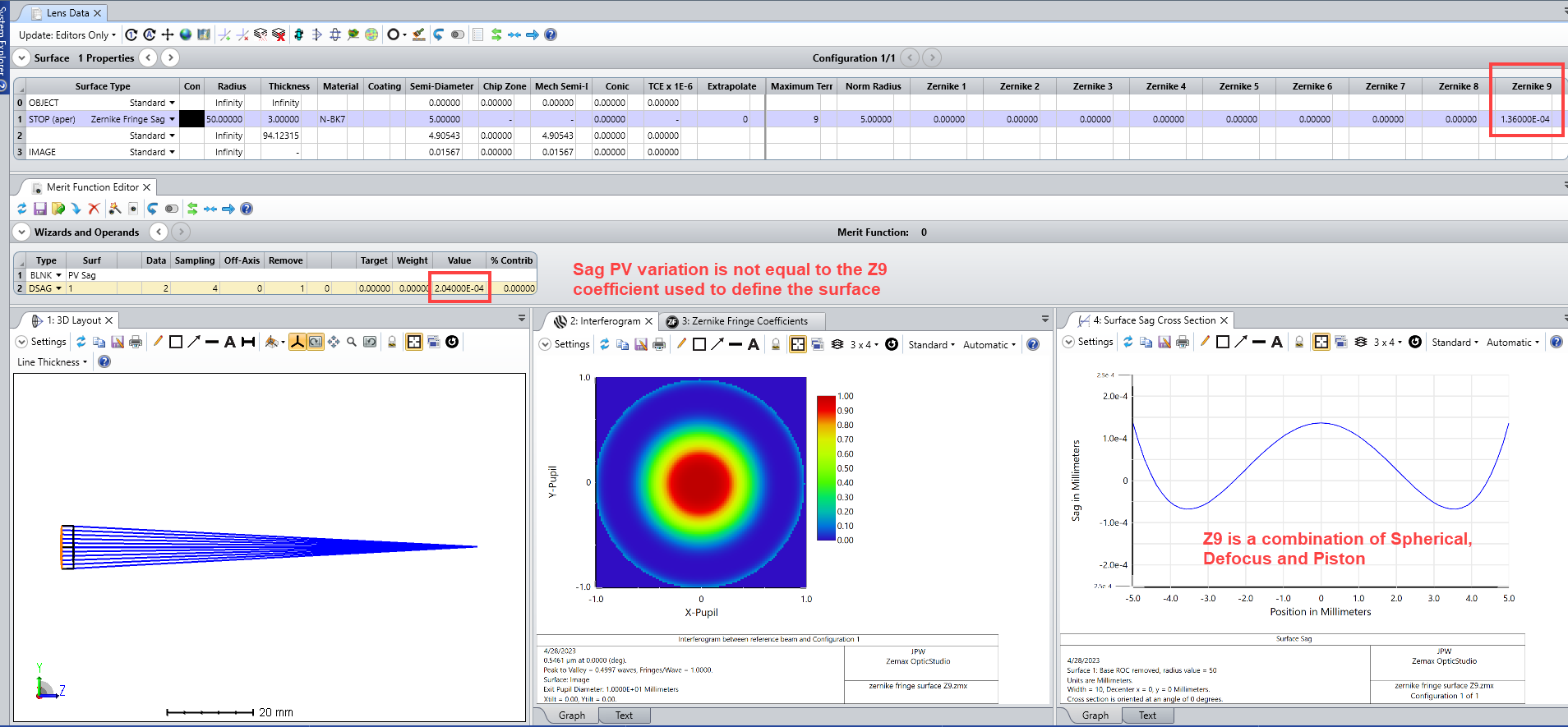
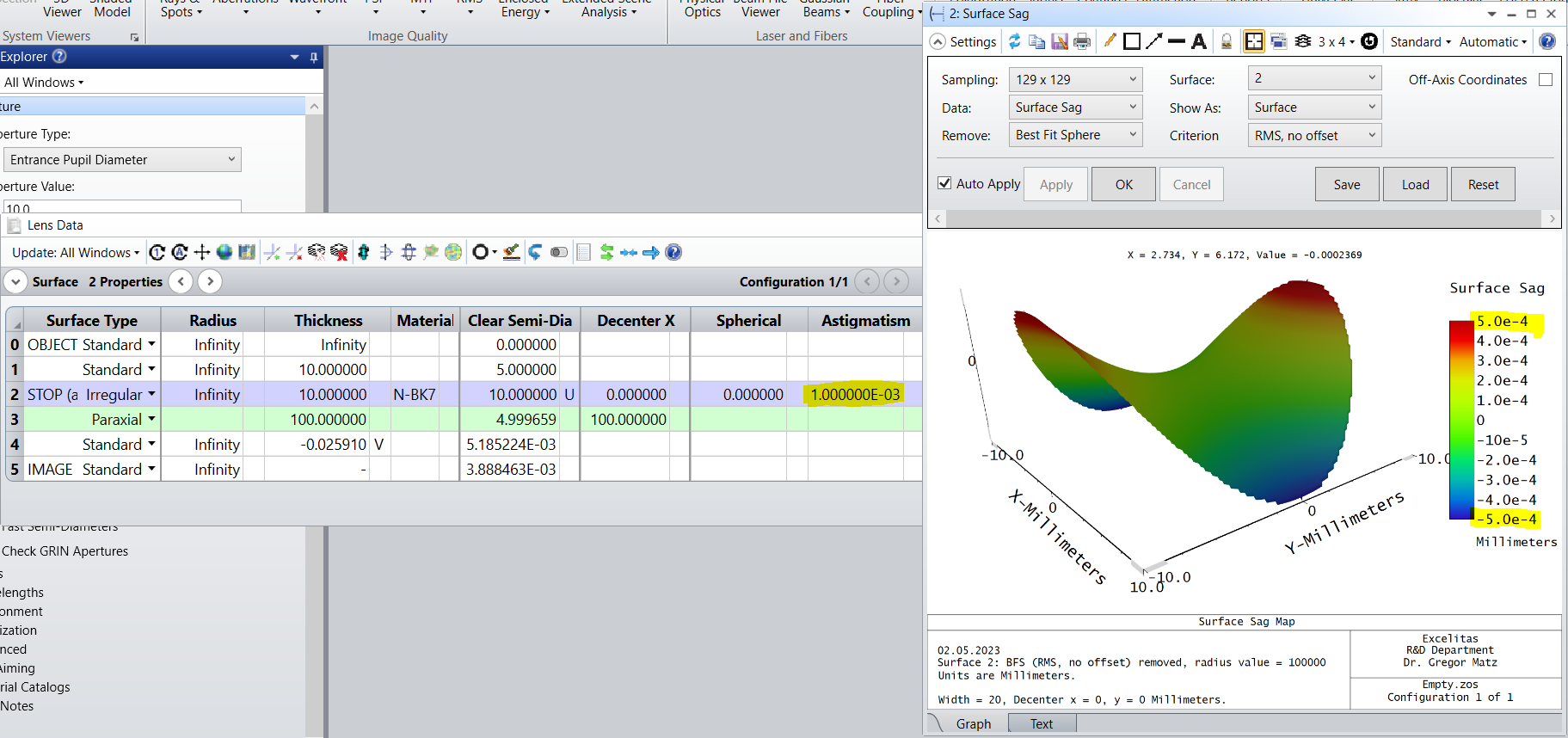
I have a question regarding the TIRR Operand in Zemax. The operand defines the sag of the surface in waves which is equally split in astigmatism and spherical aberrations. This idea is clear and often a good approach. The sag of the used irregularity surface is defined as dz=...+Zs roh^4 + Za roh_y^2 + Zc roh^2 roh_y (see Zemax-Manual). 

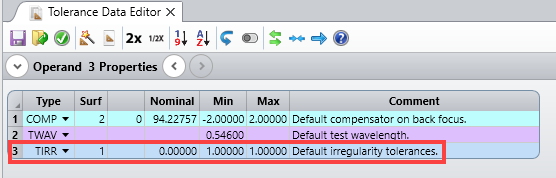
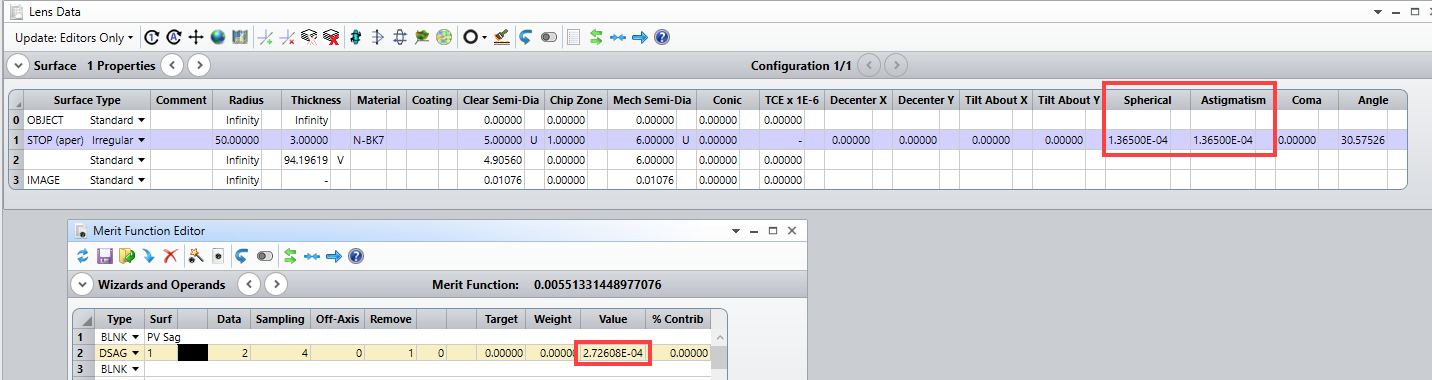
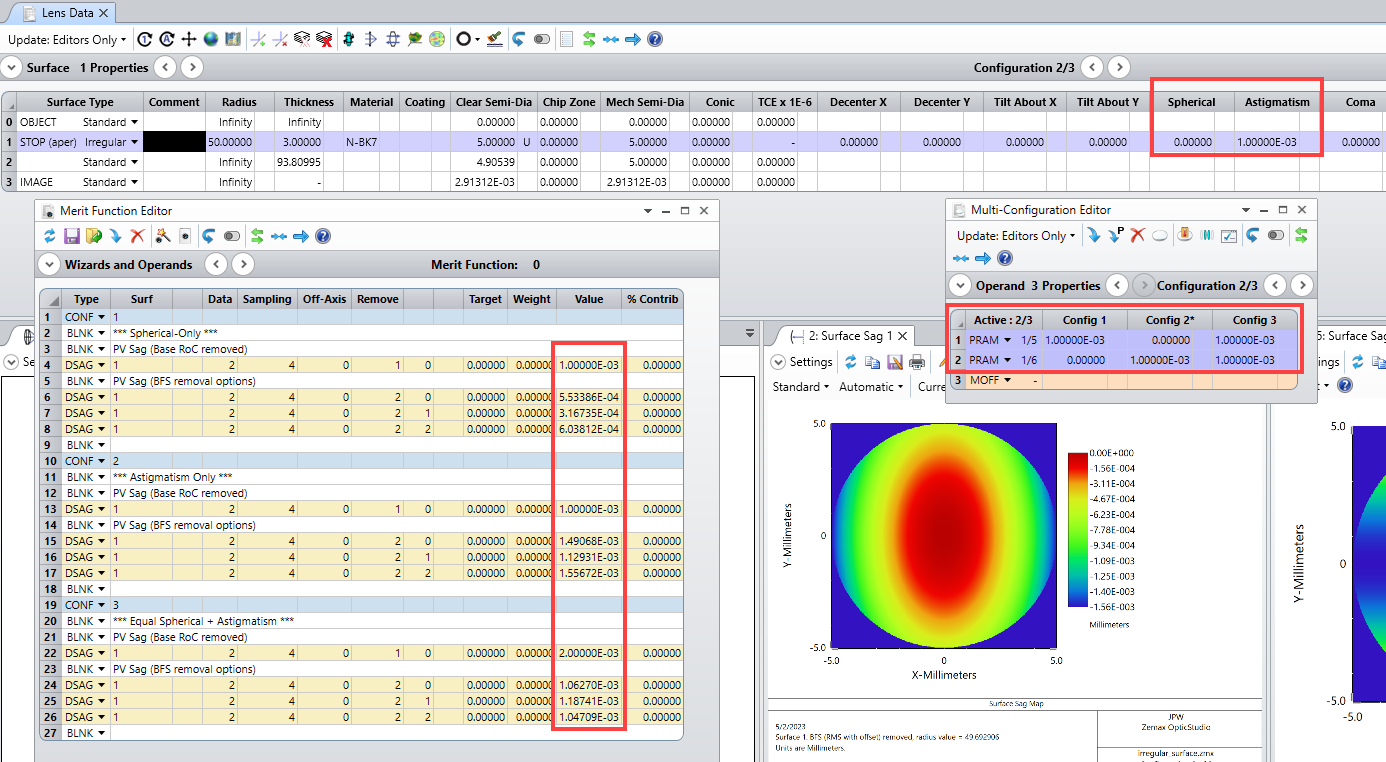
Assuming, the TIRR is 1 ring with lambda equal 546.07 nm. This leads to 0.5 rings Asti and 0.5 rings Spherical. In PV this means 136 nm (=0.5 ring/2*546.07) Asti and Spherical and hence Zs=1.36e-4 and Za=1.36e-4 (due to the fact that roh is the normalized radius).  

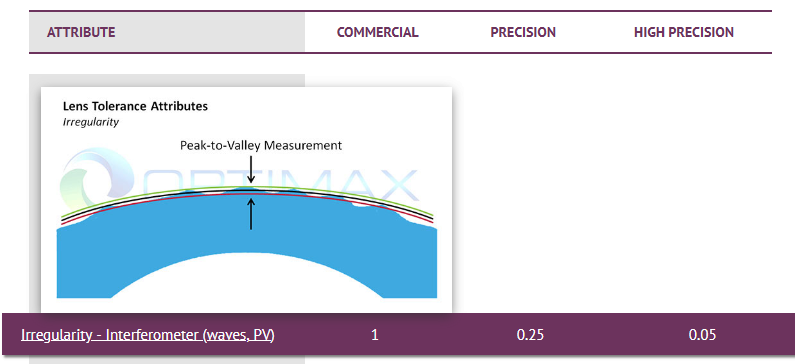
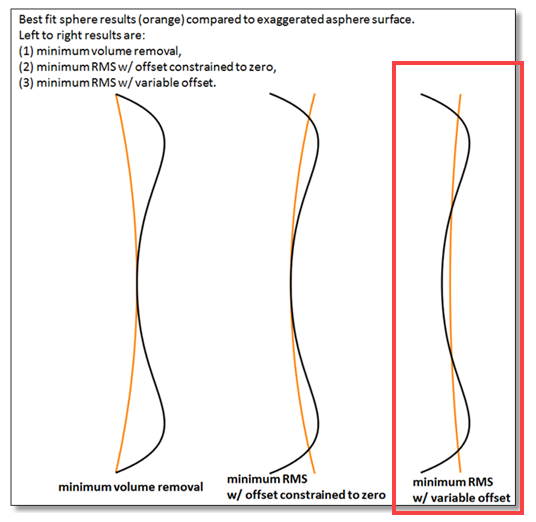
Related to the ISO10110-5, the sag of the surface is defined as 3/SAG(IRR,RSI). The IRR relates to non-spherical aberrations (for example spherical plus asti) and the RSI relates to rotational symmetric aberrations (for example spherical), both after removing the best fit sphere. In my example one might approximate this on the optical drawing as 3/-(1, 0.5) @e. 

In fact, this seems to be not the same. Asti and spherical is evaluated (acc. to ISO) as the PV of the sag after the best fit sphere is removed. If one measures 0.5 rings of Asti @e, this relates to a PV of the surface of 136 nm.  This is fine with the values listed above. Yet, if spherical aberration (with shape according to Z9) of 0.5 rings are measured, this relates to a PV of 136 nm but with the shape of Z9=6roh^4-6roh^2+1 and not with the shape of dz=Zs*roh^4. The prefactor infront of the roh^4 term is a factor 4 larger than assumed in the tolerance operand TIRR.

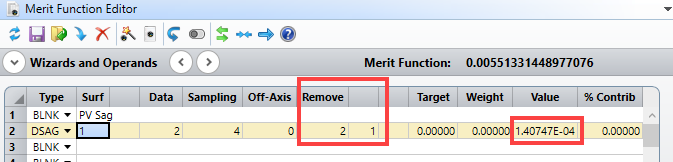
In other words: To my understanding, TIRR does not equally split Asti and Spherical but weights Asti by a factor 4 more heavy than spherical aberrations. Hence, if the RSI should be smaller than 0.5 rings, the TIRR should be set to 4 rings. In fact, this would lead to very large astigmatism simultaneously.

Is this definition intended? Or is this not inspired by the ISO10110? Is there a reason for this or do I misunderstand something?

 

Thank you and best regards!

 

Gregor

 

 

 

 

 

 

8 replies

Jeff.Wilde
Rank
Userlevel 7
Badge +3

Hi Gregor,

I think the TIRR operand properly splits the aberration equally between spherical and astigmatism.  Part of the confusion could stem from your use of the Z9 Zernike fringe term for spherical.  Actually, the functional form for this term is a combination of spherical, defocus and piston.  After subtracting the base radius (or the best fit sphere), the residual sag is *not* pure spherical.  Here is a simple example using the Zernike Fringe Sag surface:

 

However, when using the Irregular surface with only the spherical term non-zero, the value entered for spherical is indeed the correct PV value.

Regards,

Jeff

Jeff.Wilde
Rank
Userlevel 7
Badge +3

One more quick note.  If we start with a standard spherical surface, and force TIRR to apply exactly one fringe of irregularity (by setting Min = Max = 1.0):

then save a Monte Carlo file, we find that the Irregular surface has equal amounts of spherical and astigmatism, and after removing the base radius of curvature, the PV sag error is precisely one fringe (or 2.73e-04 mm in your case):

 

However, according to Optimax (and as you noted), the irregularity should be measured after removing the BFS that yields minimum RMS irregularity:

 

But if we do this using the DSAG merit function operand, the result is somewhat different:

 

I guess this is the value that should be used in an ISO 10110 irregularity spec.  So it would therefore seem that one could make a simple adjustment to the TIRR values to account for use of BFS removal (as opposed to just base radius of curvature removal).

Jeff.Wilde
Rank
Userlevel 7
Badge +3

This problem has piqued my interest.  Here’s one more follow-up.  I’m interested in confirming that TIRR: (1) does in fact split spherical and astigmatism equally, and (2) yields a PV irregularity value that depends on how power (focus) is removed from the data. 

So, I copied the two sag irregularity data sets from the previous model above into Matlab, the first with the Base RoC removed and the second with the BFS (min RMS) removed.  Then I fit each one using the first 9 Zernike Fringe polynomials (why 9? see below).  Here are the results:

I then took these Zernike coefficients and computed the amount of spherical and astigmatism (and focus) present in each irregularity data set using the formulation provided by J. C. Wyant and K. Creath (Basic Wavefront Aberration Theory for Optical Metrology, Applied Optics and Optical Engineering, Vol. XI (Ch. 1), 1992):

Note: Wyant starts numbering the Fringe polynomials at 0, while more conventionally they start at 1 (which is the format that OpticStudio follows).  So in the table above, we need to increment each Zernike index by +1 to convert to the more common format.

In any event, using the Zernike coefficients for the two data sets, I do indeed find that they both have exactly half spherical and half astigmatism of the same magnitude.  The only difference is that the second data set has non-zero focus (or power), as to be expected.

This difference in focus leads to different PV values, with the second data set having a PV irregularity that is about half that of the first data set.  Therefore, it would seem that when using TIRR for tolerancing, one should use half of the PV irregularity value utilized in the Tolerance Data Editor when constructing the ISO 10110 PV irregularity spec because the lens fabricator will likely measure a value half of the TIRR number since they should use a data set that has the BFS (min RMS) removed.

MichaelH
Rank
Userlevel 6
Badge +2

Hey Jeff,

Thanks for this really thorough explanation. 

TL;DR - TIRR should be used for test plates & TEZI should be used for interferometers and neither were developed to reflect the ISO specification.

The tolerancing algorithm was originally developed to model actual manufacturing errors and didn’t focus on a single specification (when I was first stared in optics in 2004, the MIL 13830 in the US was actually preferred over ISO 10110...it’s only in the past 5-10 years the ISO became dominate worldwide).  One should not equate an individual tolerance operand to a line on a drawing.

To add a little more background about TIRR vs TEZI, TIRR was chosen to be 50% spherical and 50% astigmatism because this is traditionally how a fabricator using a test plate would verify if an optic was “good enough”; the TEZI operand is more geared towards an interferometer where higher order errors can be quantified and an RMS value is used as the passing metric.  

TIRR should be used for full-aperture Spherical polishing where a test plate is used.  TEZI should be used for full-aperture Spherical or ¾ aperture (need to eliminate mid spatial frequency errors) Even Asphere surfaces where a (nulling) interferometer is used; Torodial surfaces are included because mathematically they can be converted but their manufacturing process does not lead to traditional Zernike-like errors.

If the fabrication process leads to mid spatial frequency errors (and the part still leads to valid Zernike calculations), then you should change the surface to a User Defined us_zernike+msf.dll and manually setup the tolerance values in the TDE.

If more complex surfaces or fabrication techniques are needed, then you should either use a Zernike Phase Surface in front of the test surface (this is the technique that the JWST used) or the new Composite Surface to decompose the individual sag errors into the actual surface:

Tolerancing surface irregularity using a phase surface – Knowledgebase (zemax.com)

Introduction to Composite Surface – Knowledgebase (zemax.com)

In my experience, the built in tolerancing is about 80-90% accurate and if you need better yield predication, then you’ll need to either add custom operands to the TDE or manually tolerance your system.  

~Michael
G

Thank you Jeff and Michael for these thorough answers!

I know that there are other ways to perform the tolerance analysis (as TEZI … ). Yet, a well established operand is/or has been the TIRR and hence my question relates to a better understanding of this operand. To use this operand might by still plausible to reflect for low order aberrations induced for example by glue tensions. Especially the last answer from you, Jeff, answers my question. Your conclusion is the following:

“Therefore, it would seem that when using TIRR for tolerancing, one should use half of the PV irregularity value utilized in the Tolerance Data Editor when constructing the ISO 10110 PV irregularity spec because the lens fabricator will likely measure a value half of the TIRR number since they should use a data set that has the BFS (min RMS) removed.”

To my understanding this means, that a TIRR of “2” correlates with 2 rings surface deformation without removing any defocus. When the defocus removal is considered, the 10110-5 spec of 3/-(1) correlates roughly with a TIRR set to “2”. This is understood. 

Yet, I still wonder about the statement in the manual that Asti and Spherical is equally considered by the TIRR. This is only true if no sphere at all is removed from the measurement. Or in other words: Defocus/Z4 is included in the wording “Spherical aberrations”. I build up a small Zemax file to visualize the difference. The TIRR uses the Irregular surface and places equal values in the column of “Spherical” and “Astigmatism”. Assuming either of both takes a value of 1e-3 (units don’t matter for the moment) this leads to:

 

PV of surface SAG: 3.19 e-4 

Assuming pure spherical aberration as in the graphic above, the resulting PV of this surface as measured in a metrology lab acc. to ISO10110 would be 2.5 e-4. The value above is at 3.19e-4 since the volume rather than the PV has been minimized. If the PV would have been optimized (option missing in Zemax, but this would be the closest to metrology), the PV would be exactly 2.5e-4. This is due to the fact that the Z9/C8 (f_Z9=6r^4+6r^2+1) has a PV of 1.5 and hence a factor 4 less than the prefactor of the r^4 term. The irregularity surface describes the function as Spherical*r^4 and hence the PV is equal the r^4 term prefactor. 

 

By considering pure astigmatism of the same magnitude in terms of the irregularity surface we get the following surface form deviation:

PV of surface SAG: 10 e-4

The prefactor of the PV of the resulting surface deviation is identical to the plugged value at the irregularity-surface which can be easily seen/shown. 

To consider Asti and Spherical equally w.r.t. the PV of the surface after removing the best fit sphere (as established in metrology since long time), the value in the column of the Irregular surface “Spherical” should be a factor 4 larger than the value in the column “Astigmatism” (at least to my understanding). As currently realized, the operand TIRR mainly reflects astigmatism with a minor weight on spherical aberrations. 

Your statement, Michael, is of course correct that “One should not equate an individual tolerance operand to a line on a drawing”. Yet, I try to get the idea behind the operand to make a connection between the lines in the drawing and the lines in the tolerance data editor at all. 

Thanks for the discussion and best regards,

Gregor

 

 

Mark.Nicholson
Rank
Userlevel 7
Badge +3

Excellent discussion here gentlemen.

Michael is spot-on with his summary TL;DR - TIRR should be used for test plates & TEZI should be used for interferometers and neither were developed to reflect the ISO specification.

Team Zemax: I think it would be a useful work package for a release to treat the issue of making tolerancing ‘speak ISO’ more. There are lots of little things that need to be addressed, but no major technical risks. Imagine a control of the tolerancer somewhere that toggles between ‘speak ISO’ and ‘use Zemax classic’. Maybe one of the columns of the TDE could be used for that, and the Wizard would have a default value. The use of ISO have blossomed to the point where it is the major format. It would also fit in with Ansys’ excellent drive to support open standards.

  • Mark

 

Jeff.Wilde
Rank
Userlevel 7
Badge +3

Yes, good discussion.  I think we all realize that there are many options for tolerancing, and they can often become fairly complicated as the complexity of the surface increases.  But with the continued push to utilize ISO 10110, I completely agree that it would be nice to update OpticStudio to make it play better with this standard (including more versatility for making lens prints!).

While TEZI is a great option when targeting an RMS irregularity spec, for a PV spec it would seem that TIRR remains quite useful -- hence the value in drilling down into the details here.  (As an aside, for aspheres, it would be nice if either TEZI or the new Composite Surface would work with User Defined us_zernike+msf.dll ; as it stands now, tolerancing with this particular UDS requires more effort than should be necessary -- but that’s going off topic from this particular thread).

For spherical surfaces, most custom lens manufacturers list a PV spec, measured via interferometry, in their tolerance table.  Case in point, Optimax (I could be wrong, but I don’t think Optimax uses test plates):

 

Regarding Gregor’s last post, I still don’t quite follow the details.  However, it’s clear that the PV irregularity computed in OpticStudio depends on the RoC of the spherical surface that is removed before computing the PV value.  For removal of a BFS, there are three options:

 

My assumption is that the lens fabricators will most likely use the third case.  Regardless, for modeling with an Irregular surface, we can use the DSAG operand to do an easy comparison of all four removal options (including the Base RoC option) when looking at three different Irregular surfaces, namely: (Config1) spherical-only, (Config2) astigmatism-only, and (Config3) equal spherical + astigmatism:

 

So it’s clear that, for a given Irregular surface, the reported PV irregularity varies with the particular spherical surface removal option.  For TIRR, with equal spherical and astigmatism parameters, it’s an easy matter to adjust for whichever removal option best reflects how the actual surface will be measured.  I’ve been using TIRR for years and never really appreciated this level of detail.  So thanks to Gregor for raising the topic!

 

Regards,

Jeff

G

Hey Mark and Jeff,

Thanks for the fast and clear feedback!

I understand the point that DSAG can be used to evaluated the spherical aberration of a surface in different ways (minimum volume removal, minimum RMS ...). Yet, the option doesn’t exist when using the TIRR to weight astigmatism vs spherical. Spherical will always be a r^4 function with the same PV as the Astigmatism. And to my understanding, this is not equally weighted.

Thanks again for the discussion. I take the feedback from my question that very often it is the better option to use TEZI for interfereometric measurements even when low order aberrations are simulated. 

Best regards,

Gregor

 

 

Reply


Community Posting GuidelinesCookie settings


Zemax Community

Need more help?

To Chinese users:

Do not provide any information or data that is restricted by applicable law, including by the People’s Republic of China’s Cybersecurity and Data Security Laws ( e.g., Important Data, National Core Data, etc.).


不要提供任何受适用法律，包括中华人民共和国的网络安全和数据安全法限制的信息或数据（如重要数据、国家核心数据等）。



Privacy policy   License Agreements    Terms of use    Cookie Policy   Zemax Account Licensing Policies