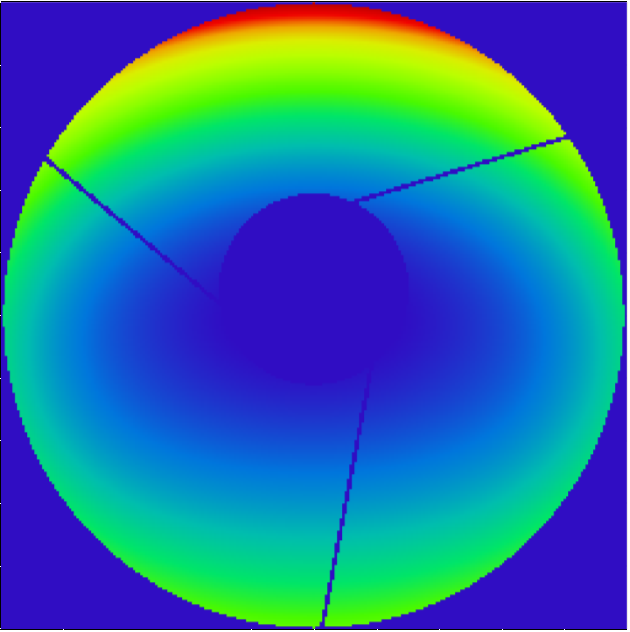
The attached file shows a wavefront with 'spiders' from a telescope.
These spiders require a very high pupil resolution for a well converging PSF calculation. But I need to calculate a huge number of PSFs and have to restrict the pupil sampling because of computing time.
Is there a possibility for 'Edge Smoothing' in Zemax? I mean a kind of 'apodization' of the spiders that yields a smooth transition from bright to dark that improves the convergence?
Additionally: The spiders and the inner obscuration are (as usual in telescopes) not in the plain of the aperture stop. Is the Zemax PSF calculation (FFT or Huygens) still valid?