A common misconception is that a ray itself (or beam of light) is s- or p- polarized. S and p are not inherent to an incoming beam of light, but are instead defined relative to the plane of incidence of the ray on a surface.

The amplitude and polarization state of the electric field is described by a vector E which has components {Ex, Ey, Ez} which are all complex-valued. The ray propagation vector k has components {l, m, n} where l, m, and n are the direction cosines of the ray in the x, y and z directions. The electric field vector E must be orthogonal to the propagation vector k so that:

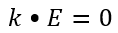
And, therefore:

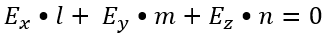
What we choose to call the x, y and z axes is arbitrary. For example, I may choose z to go from left to right across the screen, y from bottom to top, and x into the screen. Or, I might choose z to point out of the screen, y to go left to right and x to go bottom to top. As long as I am consistent in my definition of coordinate axes, there is no problem.

But, when a ray intercepts the surface of an optical component, we define a plane, called the plane of incidence, which is not arbitrary. The plane of incidence contains both the k vector and the surface normal vector n at the intercept point. The s-component of the field is the projection of E that lies along the axis orthogonal to the plane of incidence, while the p-projection lies within the plane of incidence. The electric field E is then divided into Es and Ep components, both of which are complex-valued.

So, s and p are defined relative to the plane of incidence of the ray on the surface, and are not characteristics of the beam itself.