Dear Experts,
in order to get an exact understanding of POP, I have stripped down a simulation to purely a POP simulation, i.e. without any optical element but a free-space propagation (Gaussian beam diffraction) over 1000m:

My beam definition is
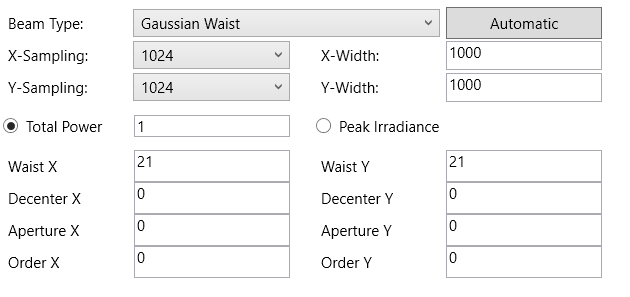
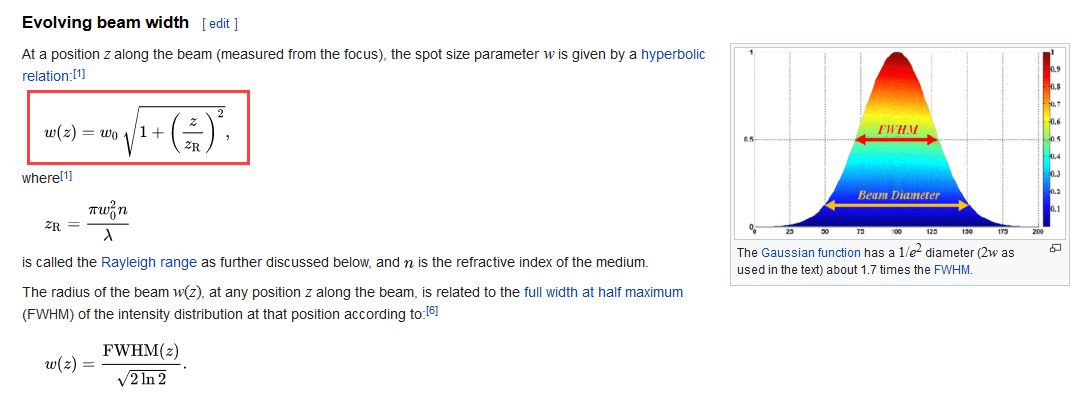
My beam waist is 21mm. Exploring that with the Beam File Viewer, this is a 21mm radius at 1/e². However, in the help file I find

where w_0y (omega) should be the same as Waist X?! According to these formulas this would be a 1/e radius (not squared), if I do the math right. Maybe w_0y is not equal to Waist X?
According to Teich/Saleh a 21mm 1/e² radius Gaussian beam should result in a divergence theta of (omega_0 is the 1/e² radius)
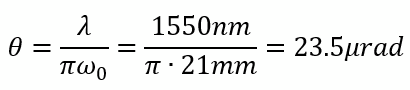
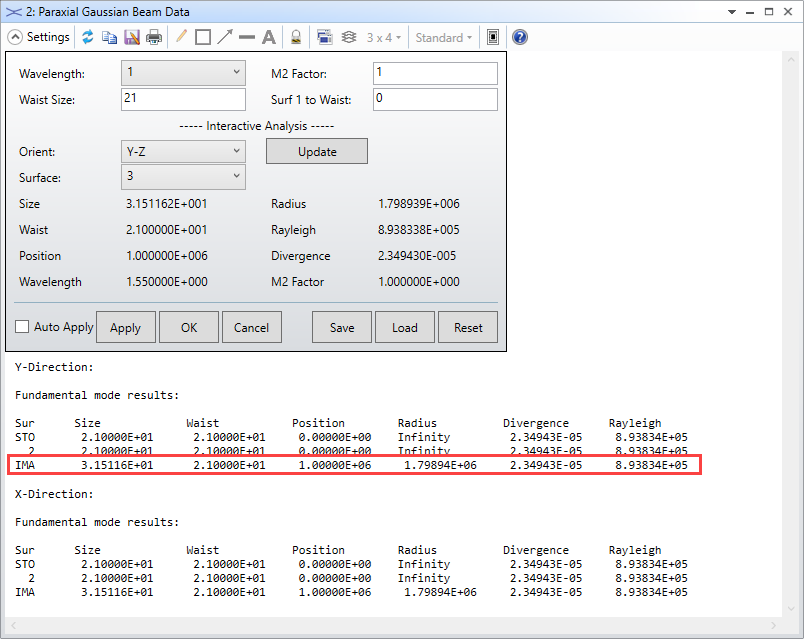
i.e. my beam should have a radius of 23.5mm after 1000m propagation.

Reading from the cross section in the image plane, I get around 31mm at 1/e², so a difference of 7.5mm to the expected 23.5mm.
It would be great to get a hint, if my modelling of such a minimal system, i.e. only the Gaussian beam diffraction, is correctly done in Zemax. I attach my file.
Many thanks. Any advice would be very welcome
Markus