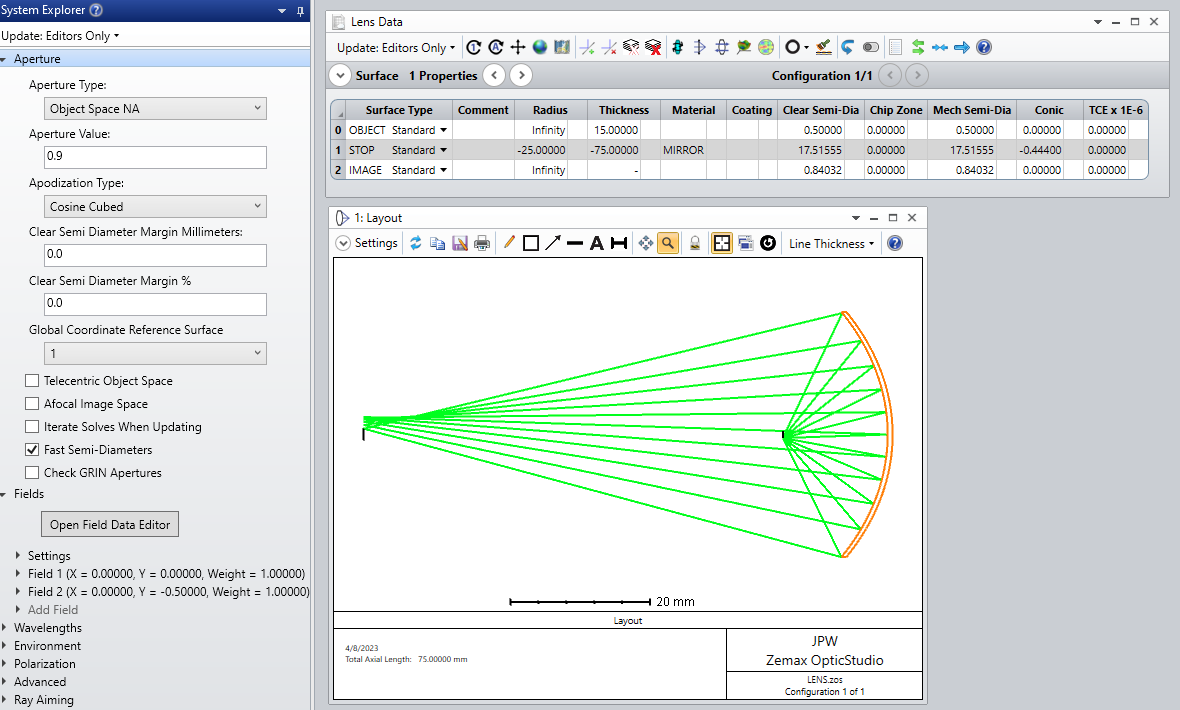
Is it possible to calculate space mapping of the light source (LED) radiance distribution onto the target irradiance distribution in Zemax?
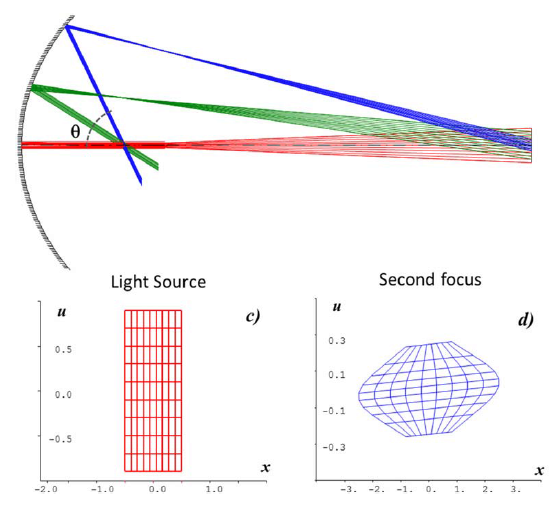
For example, I found the article (link) where authors performed phase space transformation by local ABCD matrixes in CodeV using differential ray tracing function. They traced reference rays and found exact location of the radiance (irradiance) patches, whereas the surrounding local ABCD transformation defines the shape of the radiance patch in phase space and the projection defines the irradiance contribution, respectively.
So basically I want to do the same in Zemax:
- Get radiance of the source (light source mapping).
- For direction vetor (L,M,N) calculate ray r which corresponds to a pair of xu-values, where angular variable u is associated with the angle u = n × sin θ of a ray relative to optical axis.
- Find ABCD matrix for source→ target mapping.
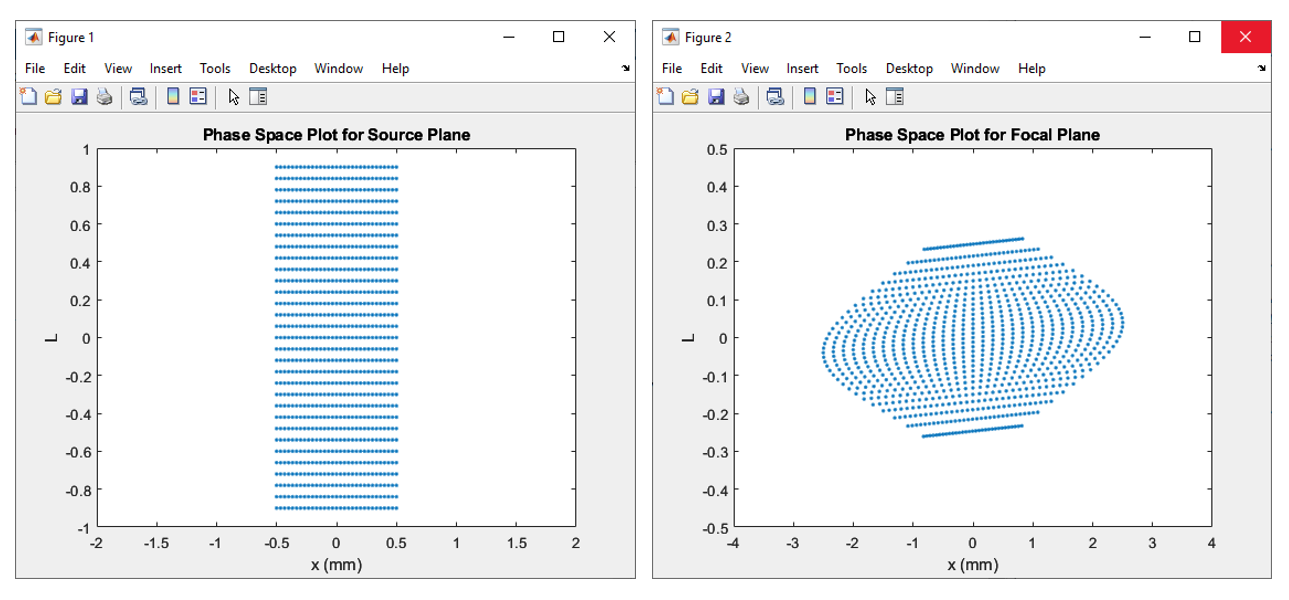
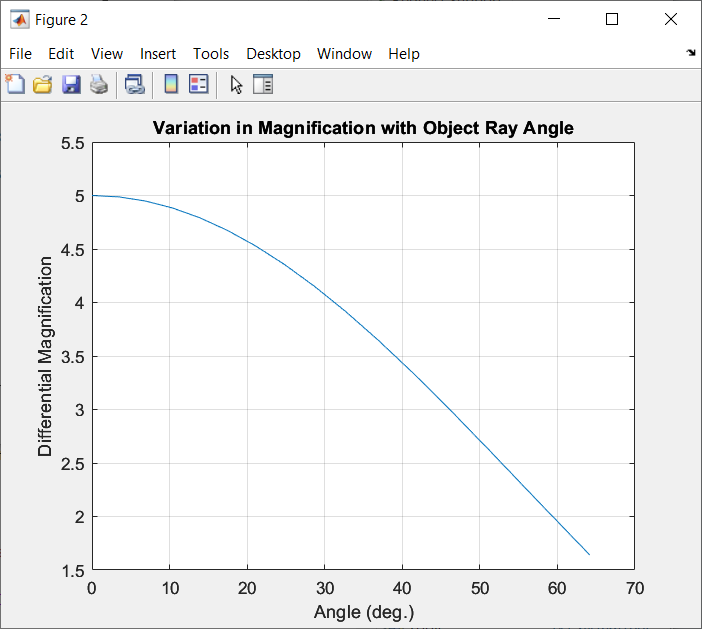
- Calculate radiance L(x,u) on the target plane (xu-diagram, phase space devided into equal areas).
- Insert optical element to change irradiation pattern (for example, Lambertian → uniform )
- Optimize the position of the reference rays r and repeat steps 2-4.
I would apreciate for any hints towards implementation of phase space mapping in Zemax (sequential and non-sequential modes) using ZOS-API or ZPL marcos.
P.S. I’ve already tried to calculate ABCD matrix for thick lens as Mr. Sahil described here.
Perhaps, by modifiying this method for calculation of radiance distribution and E-field for transmitted and reflected rays, we could implement ray tracing function for irradiance
distribution in phase space.