How can I design a microscope with two thick lenses in zemax? I want a magnifiaction of at least 2 for my system.
Best answer by David.Nguyen
View original
Designing a microscope
Userlevel 7
+2
Hi Sajed,
That is a pretty broad question. I’ll try to give you some clues and hopefully you can manage to achieve your goal.
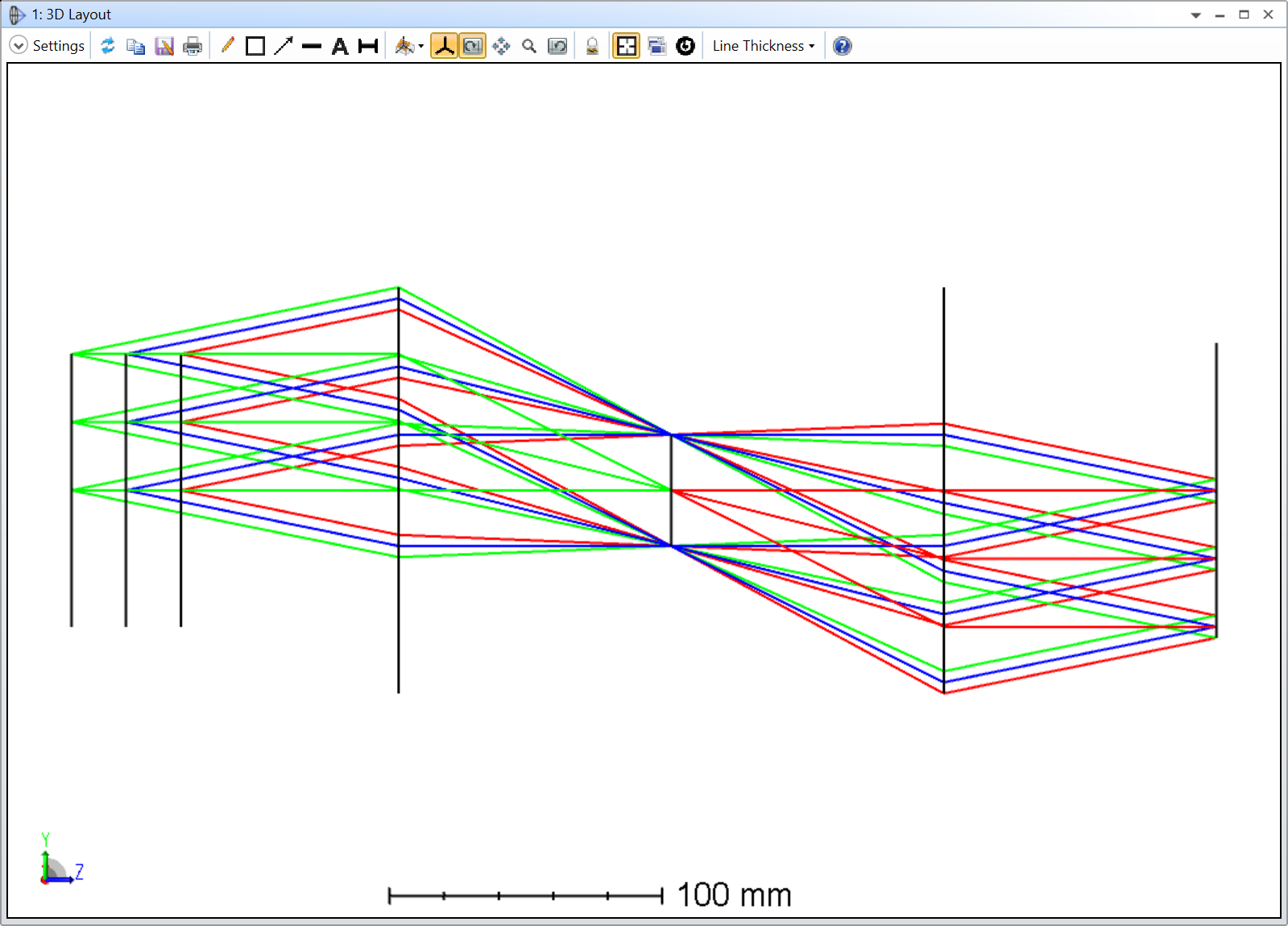
Since you want to use two lenses, I’m assuming it is for an infinity system. In this case, the magnification is given by the ratio of the lenses focal lengths. If you want a magnification of 2X, you could use an “objective” (sample size) lens with a focal length of 100 mm and a “tube” (user or camera side) lens of 200 mm for example (200 / 100 = 2X). The longer the focal length, the longer the overall microscope. However, short focal length lenses typically have worst tolerances (they are harder to manufacture due to the curvature of its surfaces).
The other thing to keep in mind is the kind of resolution you’d like to achieve. In microscopy, people use the numerical aperture to compute an estimate of the resolution (have a look at this article). The longer the focal length, the smaller the numerical aperture for a given lens diameter, thereby limiting your resolution. In the example I’ve attached to my answer, I constrained the aperture STOP diameter to achieve a diffraction-limited design.
Once you’ve settled for the lens focal lengths and diameter, I’d browse the catalog lenses. In my example, I used THORLABS lenses (100, and 200 mm focal lengths).
The Merit Function in my example is just a spot criterion with two REAY and DIVI operands for the magnification. I take the ratio of the off-axis chief ray Y-coordinate in object, and image space as the magnification. I’ve added RAID operands to control the telecentricity of the system. It is not strictly necessary, but that is often the case in infitiy systems.
Note the orientation of the lenses, you typically want the more curved surfaces towards the parallel ray bundles.
Finally, there are so many more considerations when designing a microscope to be discussed that any forum answer would fall short to cover everything. As you progress with your design, I suggest you ask more specific questions when needed. This will increase your chances of getting a response.
Take care,
David
Hi David,
Thanks so much for your response. Sorry for my short question, but I frustrated and I didn’t know how to start build a simple microscope. Your answer was to the point though.
Appreciate the help!
David,
I have two questions about the telecentricity function you have defined in the merit function. First, you are using Real ray angle of incidence (RAED) in the merit function. How is it related to telecentricity?
Second, you are defining some Hy values of 0.9,0.8,0.5, and zero for the RAID. How did you come up with those certain Hys. Are they some random numbers?
Warm regards,
Sajed
Userlevel 7
+2
Hi Sajed,
In conjugate systems (those that form an image of an object, such as a microscope) telecentricity referes to the ability of the system to produce a constant magnification along the optical axis on either side of the system.
That means, if you move your object closer to the objective lens, it will be blurry, but it’ll still retain the original magnification. I’ve illustrated this phenomenon with a 4f system (two paraxial lenses separated by the sum of their focal lengths, the object is at a focal length distance before the first lens, and the image is formed a focal length away from the last lens), which is the configuration used by infinity-corrected microscopes:
I have used three configurations. The blue configuration is focused on the image plane, red and green are defocused by moving the object position. As you can see, red and green are defocused in the image. But the magnification stayed the same. The reason behind this behaviour is that the chief rays at the different field position are all parallel, and in this case, they are even paraellel to the optical axis. That is why in your microscope you can use an operand such as RAID to force the chief ray (Px = 0.0, Py = 0.0) angle to be zero (parallel to the optical axis). Now, you want to do that for all the fields defined by Hy (I’m only doing Hy if I know the system is rotationally symmetric). Hy varies between -1 and 1, but again if the system is symmetric, I can afford to only care about the 0 to 1 interval. How should you sample this interval? Well, its a little bit like the Gaussian quadrature, which is used in the Merit function. You don’t actually want to have a uniform field distribution because the rays closer to 1 will contribute more to degrade the telecentricity. Therefore, I tend to use those arbitrary values: 0.0, 0.5, 0.8, 0.9. In practice, I don’t include 1.0 because it is at the very edge of the field, which is relatively more aberrated already (think about field curvature for example in microscopy). You could use more operands also, but the more operands you add, the slower the Merit function calculation.
I hope that sort of makes sense :p
Take care,
David
That make sense .
Thanks for your clear response!
Warm regards,
Sajed
Reply
Enter your username or e-mail address. We'll send you an e-mail with instructions to reset your password.
Need more help?
To Chinese users:
Do not provide any information or data that is restricted by applicable law, including by the People’s Republic of China’s Cybersecurity and Data Security Laws ( e.g., Important Data, National Core Data, etc.).
不要提供任何受适用法律，包括中华人民共和国的网络安全和数据安全法限制的信息或数据（如重要数据、国家核心数据等）。