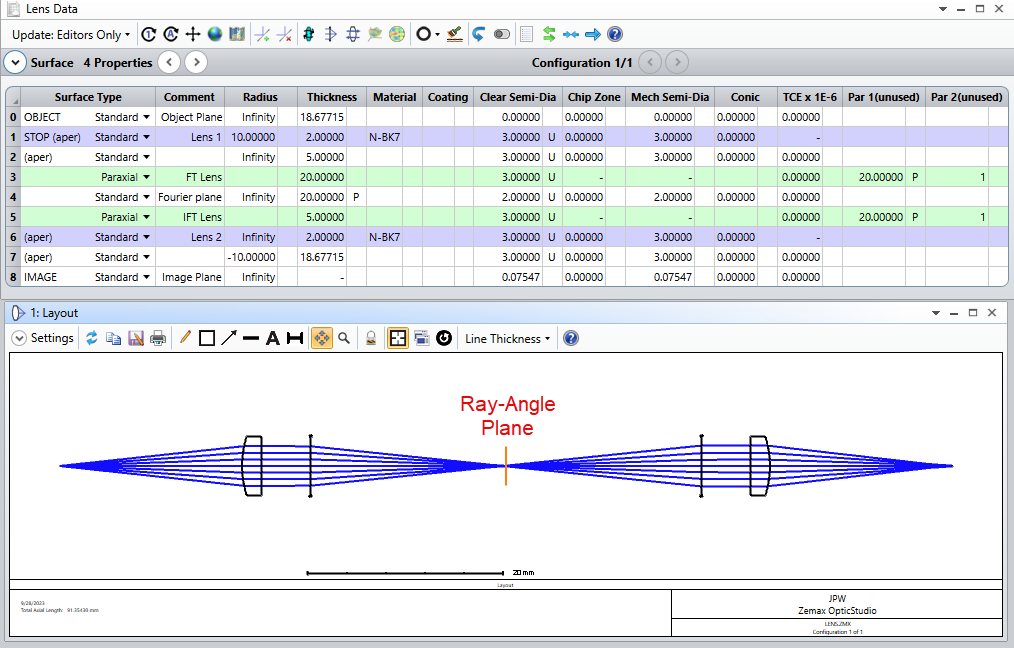
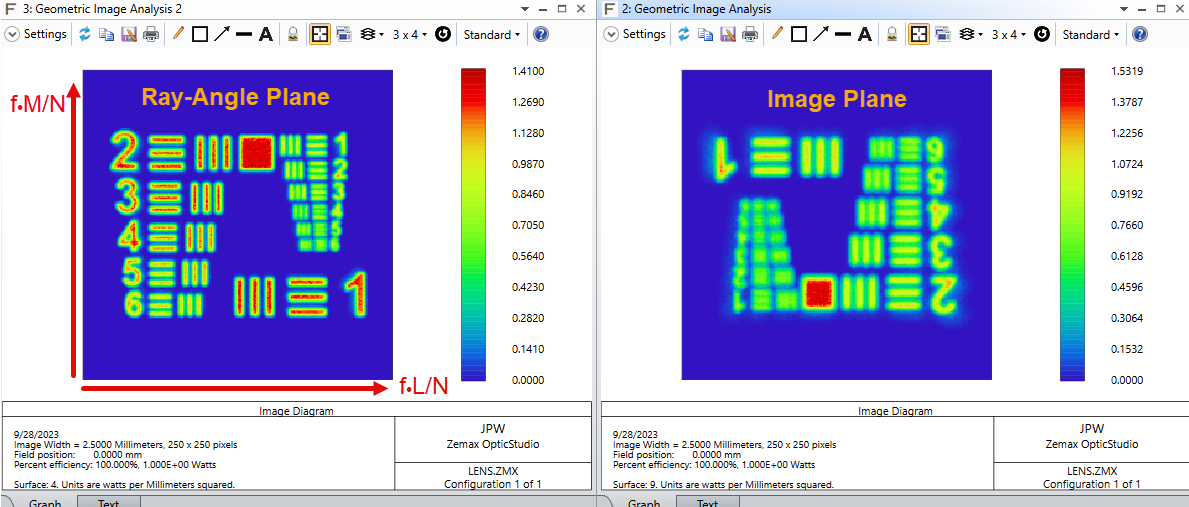
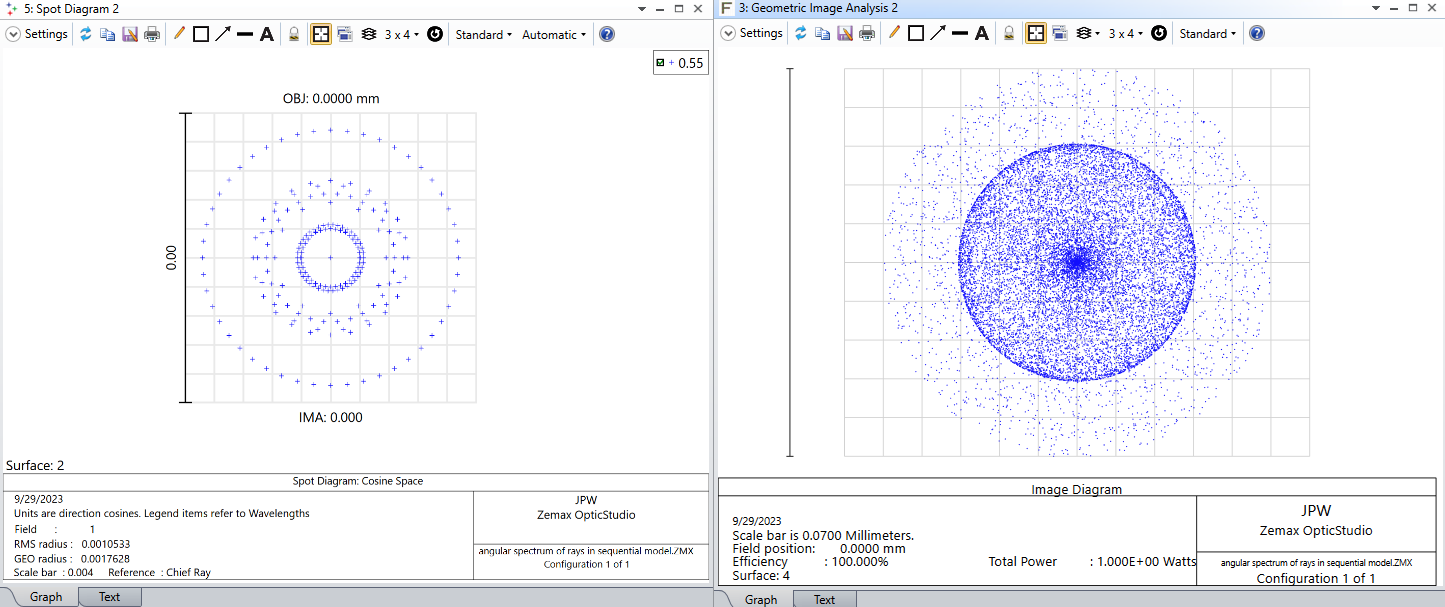
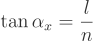An optical system composed of two lenses operates between two finite conjugate planes. The first lens collimates the image from the object. The second lens focuses the collimated image into an image.
I would like to extract the angular spread of the rays in the collimated space. How can that be done in sequential mode? Is it possible to set up a detector betwen the two lenses?