Hi Yvan,
The OPD mode indicates how OpticStudio should calculate the optical path difference for rays refracted by the paraxial lens.
If the Mode = 0 the OPD computation is based upon the conjugate positions computed by tracing a real parabasal ray. Mode = 1 integrates the actual phase introduced by the surface for each ray traced. Mode = 2 assumes that the lens is used at infinite conjugates regardless of the actual conjugates. Mode = 3 is similar to Mode = 0, except paraxial rather than real rays are used.
You can read a complete description of how this modes work browsing the help files as such:
The Setup Tab > Editors Group (Setup Tab) > Lens Data Editor > Sequential Surfaces (lens data editor) > Paraxial (sequential surfaces, lens data editor)
The paraxial surface acts as an ideal thin lens.It means that light from any given point on an object would pass through the lens and come together at a single point in the image surface, so there is no deviation from the idelized lens performance (Aberrations).
Lastly, the difference between the MTF on and off axis is because the Working F/# is different for on axis and off axis field. For focal systems, the cutoff frequency at any one wavelength is given by one over the wavelength times the working F/#.
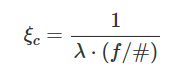
OpticStudio computes the working F/# at each wavelength for each field for the sagittal and tangential response separately. You can check with the optimization operands SFNO and TFNO that they are different for both field points, and therefore, the MTF curves are not the same: