Hello
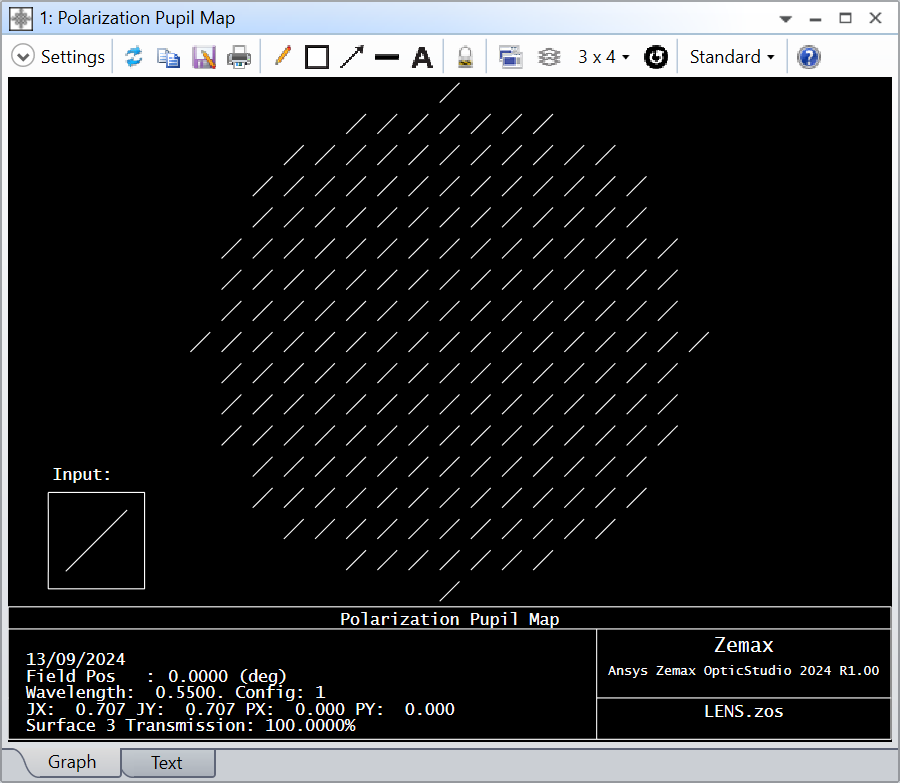
I want to simulate the effect of a quarter wave plate that creates an additional shift in the polarization of lets say 10° in a plarimeters. The polarimeter is comprised of a lens, collimating the polarized beam, a quarter wave plate, and an analyser plate. To determine the polarization state, the quarter wave plate is rotated azimutally by 180°. With the data I calculate the stokes parameter. It all works fine for the ideal case, but not for an added phase shift between both polarization states.
I am using the Jones matrix for the exact quarter wave plate in the form of:
A_real=1
A_img=0
D_real=0
D_img=1
the result for this quarter wave plate is as expected. The result is the same when I use, for testing purpose, the non-factored version Jones matrix of the quarter wave plate:
A_real=0.707
A_img=0.707
D_real=0.707
D_img=-0.707
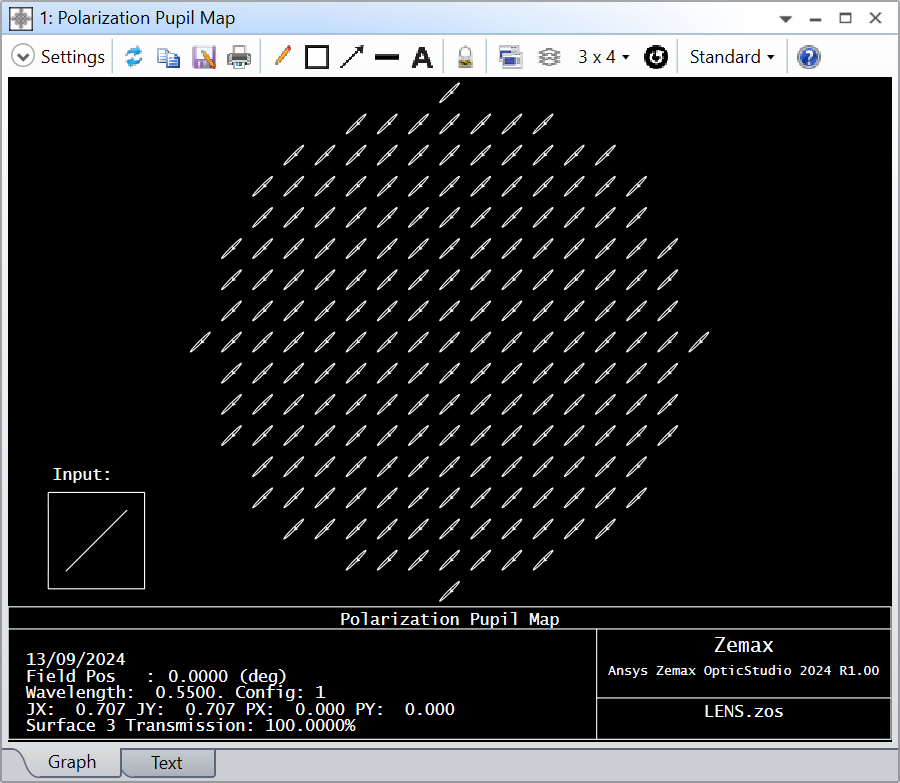
Now I add to the lambda/4 phase shift an additional shift of 10° in the Jone matrix, which results in the Jones matrix in Zemax notation:
A_real=0.573576
A_img=0.819152
D_real=0.573576
D_img=-0.819152
With this Jones matrix I get a lower system transmission (stokes parameter S0) than before and a polarization degree beyond 1 (stokes parameter S1).
Can anyone help with getting the correct Jones matrix for an “arbitrary” phase shift (e.g. retarder plate)?