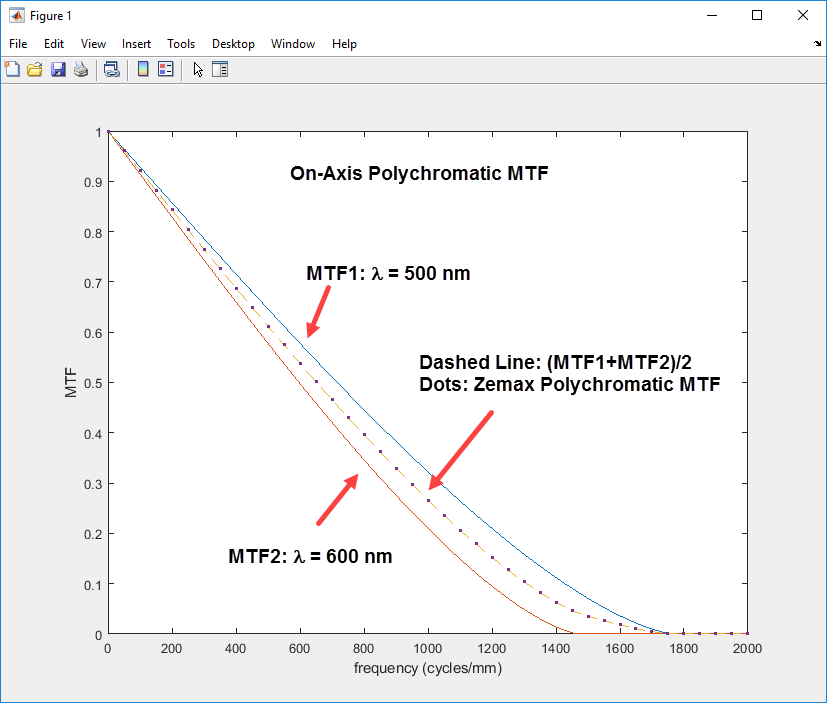
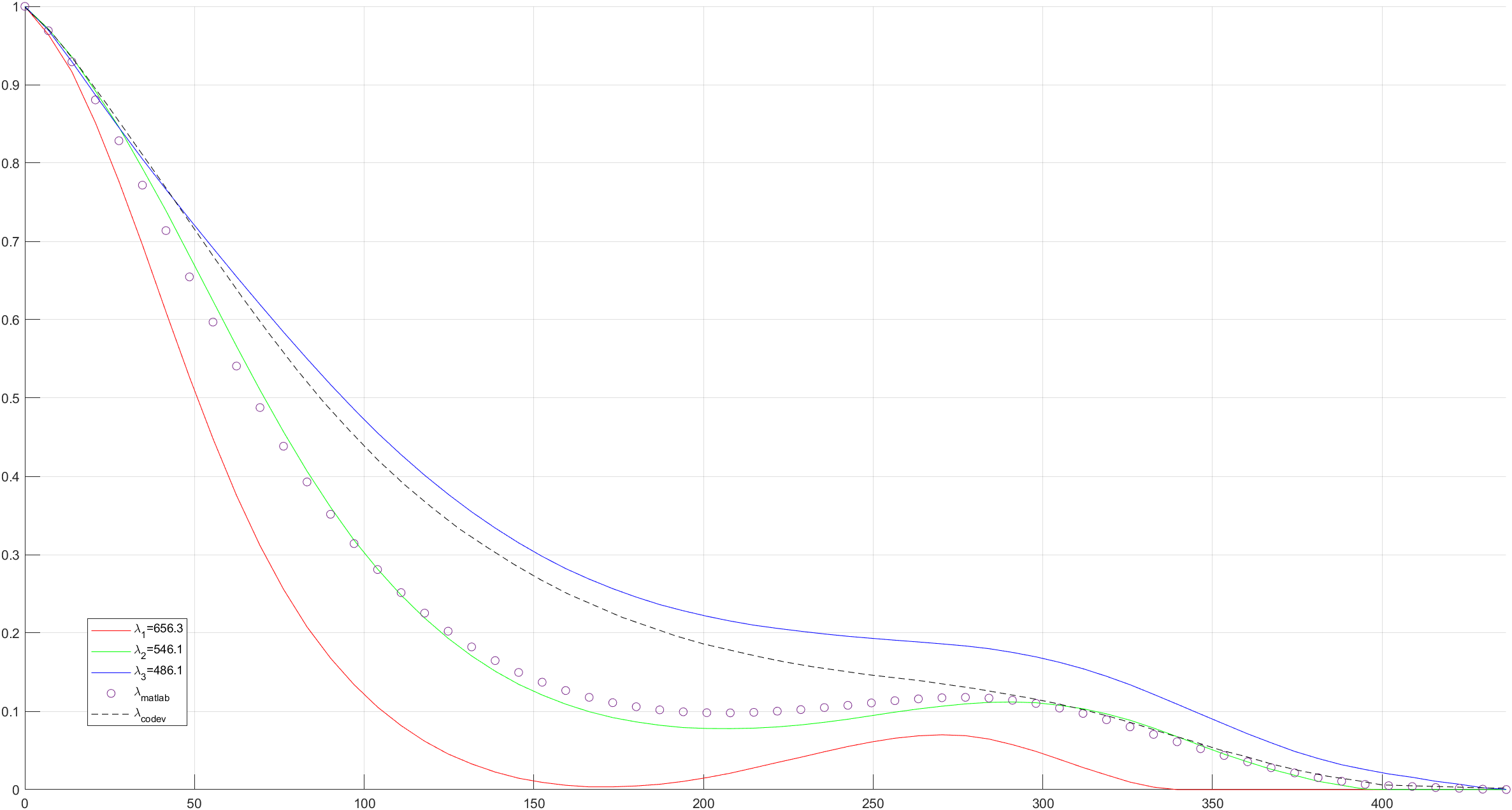
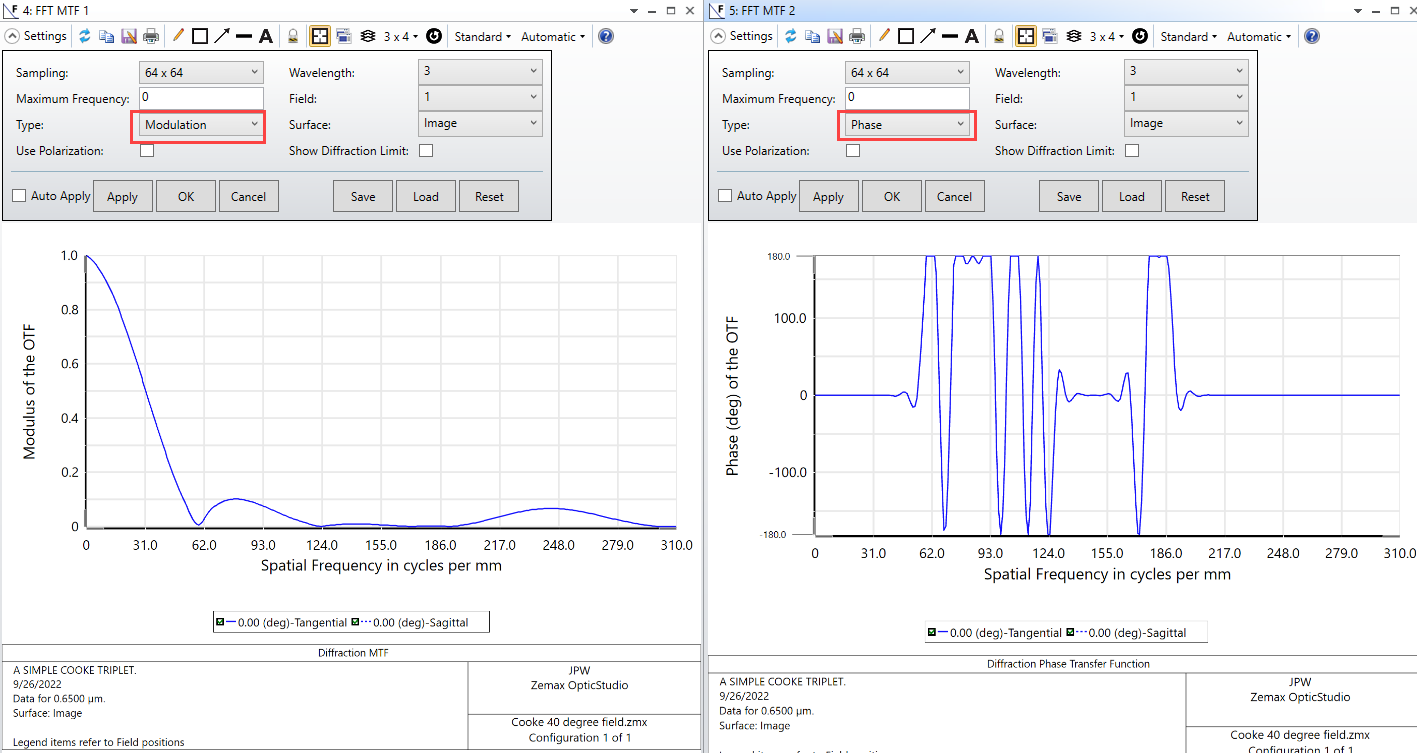
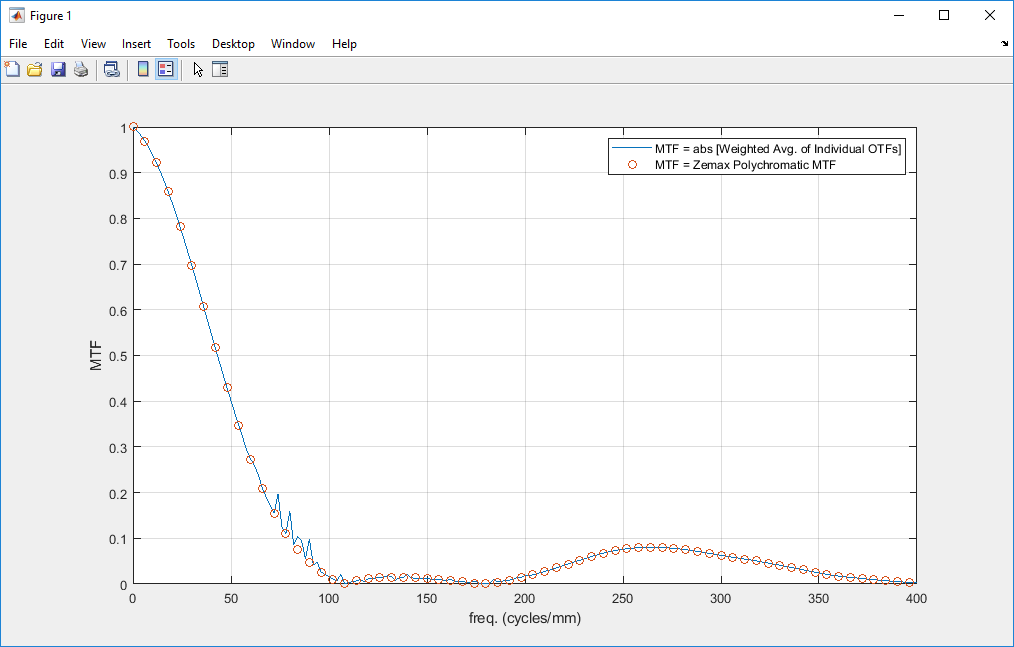
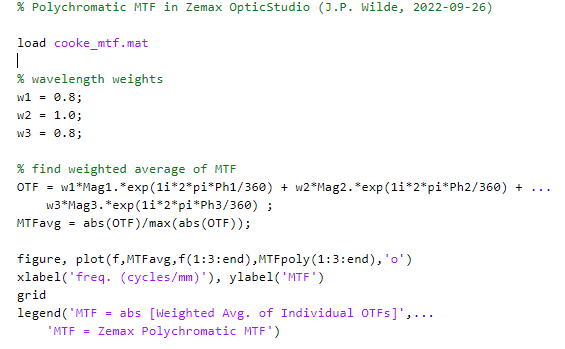
While the MTF at each individual wavelength in your system may be good, if the system has some chromatic aberration then this means that the individual wavelengths are offset from each other. Therefore, when the results of the individual wavelengths are combined you will get a reduced value of the polychromatic MTF.
Let's say, for example, that you have excellent monochromatic modulation, say 90% at each of three wavelengths individually. But if you have lateral color, the peaks and valleys of each wavelength are offset from each other. The polychromatic intensity modulation gets reduced since it never goes as low as the individual monochromatic intensities do. So you may get a much lower modulation, like 40% polychromatically.